Расширение понятия числа. Комплексные числа, действия над ними

Вспомним известные из школьной программы числовые множества и арифметические действия, которые в них определены.

Прежде всего, это множество натуральных чисел N, в котором возможны сложение, умножение и возведение в степень с натуральным показателем. Такие, например, действия как вычитание и деление не всегда возможны над числами из N, если результат должен снова принадлежать N.

Если присоединить к N число нуль и все целые отрицательные числа, то получим множество целых чисел, обозначаемые Z. Целые числа удобно изображать на числовой оси равноотстоящими точками.

Для любых целых чисел операция вычитания уже определена, но операция деления для некоторых пар целых чисел приводит к результату (числу), которого нет в Z.

Присоединим к Z все дроби (числа вида , -любые целые числа, ). Полученное множество обозначают через 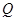и называют множеством рациональных чисел. Заметим, что при 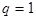получаются целые числа.

Во множестве 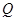можно выполнять все четыре арифметических действия (сложение, вычитание, умножение, деление на число отличное от нуля), но, например, операция извлечения квадратного корня не всегда приводит к рациональному числу. Например, не является рациональным числом.

Известно, что всякое рациональное число можно представить в виде бесконечной периодической десятичной дроби и, наоборот, каждую такую дробь можно записать в виде рационального числа.

Существуют числа, называемые иррациональными, для которых запись в виде бесконечной периодической десятичной дроби невозможна, например, 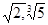и т.д.

Присоединим все иррациональные числа к множеству 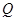, получим множество вещественных чисел, обозначаемое .

В операция извлечения корня возможна для положительных чисел. Вещественные (действительные) числа геометрически изображаются точками на числовой оси таким образом, что между всеми вещественными числами и точками оси существует взаимно-однозначное соответствие.

Рассматривая уравнение , мы обнаруживаем, что оно не имеет решений, хотя никаких видимых причин для этого нет.

Расширим множество вещественных чисел так, чтобы в новом множестве чисел уравнения, аналогичные вышеуказанному имели решение.

Упорядоченную пару действительных чисел () называют комплексным числом.

Геометрически комплексное число изображается точкой плоскости 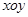. В декартовой системе координат числа и являются ее координатами. Так что числа вида - это действительные числа, т.е. множество действительных чисел входит в множество C комплексных чисел.

Число 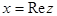называется реальной (вещественной) частью комплексного числа , а число - мнимой частью этого комплексного числа.

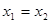Два комплексных числа и называются равными, если равны их действительные и мнимые части, т.е. , если и . Соотношение больше–меньше для комплексных чисел не вводится.

Определим действия над комплексными числами.

Пусть , . Положим по определению

(1)

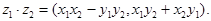(2)

Легко убедиться, что в частном случае, когда числа действительные, т.е. 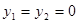, формулы (1,2) не противоречат обычным действиям над действительными числами (убедиться в этом самостоятельно).

Легко также убедиться, что коммутативный закон сложения и умножения выполняется и для комплексных чисел, т.е. и .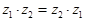

Выполняется и дистрибутивный закон

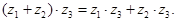
Умножим число само на себя. Воспользовавшись (2), получим . Итак, квадрат комплексного числа равен минус единице. Это число называют мнимой единицей и обозначают так 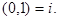Таким образом, т.е. в множестве комплексных чисел возможно извлечение квадратного корня из отрицательного числа.

Используя мнимую единицу , можно комплексное число записать в другом виде. Действительно,

Получили, так называемую, алгебраическую форму записи комплексного числа. Если комплексные числа записаны в алгебраической форме, то действия над ними можно осуществлять, как аналогичные действия над многочленами, учитывая только, что

Комплексные числа 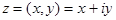и называются взаимно сопряженными.

Деление комплексных чисел вводится следующим образом

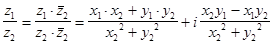. (3)

Пример.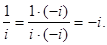

Уточним теперь определение комплексных чисел.

Определение. Элементы множества упорядоченных пар действительных чисел для которых введены арифметические операции по правилам (1), (2), (3), называются комплексными числами.

§ 2. Тригонометрическая и показательная формы комплексного числа

Как уже отмечалось, геометрической интерпрета-цией комплексного числа является точка на плоскости. Положение точки определяется ее радиус-вектором . В декартовой системе координат положение точки определяют ее координаты и . В полярной системе координат положение точки определяют координаты: – угол между осью и радиус-вектором и расстояние от начала координат до точки. Связь между декартовыми и полярными координатами следующая:

, . Учитывая это, комплексное число можно записать в виде

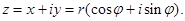(1)

Формула (1) дает еще одну форму записи комплексного числа - тригонометрическую. При этом называется модулем комплексного числа, а угол - аргументом комплексного числа. Заметим, что угол определяется не однозначно, а с точностью до периода , поэтому вводят понятие главного значения аргумента - 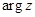. Так что , .

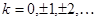Будем считать, что 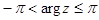, тогда

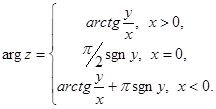где

Пример 1. Представить числа , 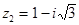в тригонометрической форме.

Решение.

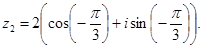
Умножим два комплексных числа, записанные в тригонометрической форме.

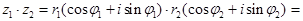
(2)

Как видно из формулы (2), при умножении чисел их модули перемножаются, а аргументы складываются. Правило это распространяется на любое число сомножителей. В частности, если получим

(3)

Формула (3) называется формулой Муавра.

Аналогично можно убедиться, что при делении чисел их модули делятся, а аргументы вычитаются (убедиться в этом самостоятельно).

Рассмотрим действие извлечения корня n-ой степени (n – натуральное) из комплексного числа. Предположим, что в результате извлечения этого корня получится опять некоторое комплексное число.

Найдем неизвестные 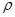и . Для этого возведем обе части полученного равенства в n-ю степень. Используя формулу Муавра, получим, что

(4)

Равные комплексные числа имеют равные модули, а аргументы отличаются на 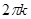. Поэтому из (4) следует

; .

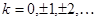Итак, (5)

Можно убедиться, что формула (5) дает ровно n различных корней при .

Пример 2. Найти .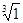

Дата добавления: 2014-12-27