Плоские кривые второго порядка

В предыдущем параграфе мы убедились, что прямая на плоскости в декартовой системе координат имеет уравнение первой степени. Справедливо и обратное утверждение - всякое уравнение первой степени геометрически представляет собой прямую линию.

Плоские кривые, которые задаются алгебраическими уравнениями второй степени, называются кривыми второго порядка. Это - эллипс, гипербола, парабола.

Определение 1. Эллипсом называется множество точек плоскости, для каждой из которых сумма расстояний до двух фиксированных точек плоскост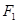и и 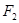, называемых фокусами, есть величина постоянная.

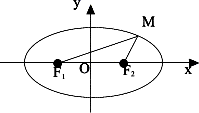
Найдем уравнение эллипса. Прямую, на которой лежат фокусы, примем за ось x. Ось y проведем через середину отрезка перпендикулярно ему.

Положим 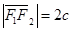, тогда фокусы будут иметь следующие координаты 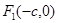, . Если - произвольная точка эллипса, тогда согласно определению,

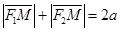, (1)

где 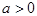-некоторый параметр. Т.к. сумма двух сторон треугольника всегда больше третьей, то 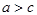. Поскольку , , то подставляя эти векторы в уравнение (1), получим искомое уравнение эллипса

. (2)

Упростим уравнение (2). Уединяя первый корень и возвышая обе части уравнения в квадрат, получим

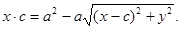
После повторного уединения корня и возведения в квадрат найдем, что . (3)

Поскольку 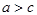, то введем обозначение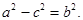

С учетом этого, уравнение (3) примет вид

. (4)

Уравнение (4) называется каноническим уравнением эллипса.

Замечание. Возведение в квадрат, вообще говоря, нарушает равносильность уравнения. Могут появиться лишние корни, т.е. точки не принадлежащие эллипсу. Однако, в данном случае уравнения (2) и (4) равносильны.

Рассмотрим некоторые свойства эллипса. Пусть точка принадлежит эллипсу, тогда точка 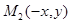также принадлежит эллипсу в силу четности уравнения (4) по переменной 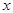. А это означает, что ось oy является осью симметрии. Аналогично можно убедиться, что ось Оx является осью симметрии эллипса. Точка пересечения осей симметрии является центром симметрии. Поэтому эллипс называется центральной кривой второго порядка.

Из (4) найдем откуда следует, что Аналогично найдем, что 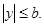Таким образом, эллипс целиком расположен в прямоугольнике со сторонами 2 и 2 . Величины и называют полуосями эллипса. Та полуось, на которой расположены фокусы, называется большой, а другая - малой. Величина

(5)

называется эксцентриситетом эллипса. Если 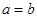, то эллипс превращается в окружность, а эксцентриситет обращается в нуль. Если малая полуось уменьшается до нуля, то эксцентриситет увеличивается до единицы. Таким образом, эксцентриситет показывает степень сплющенности эллипса.

Найдем параметрические уравнения эллипса. Возьмем две концентрические окружности с радиусами и . Под углом к оси Оx проведем луч. Из точек пересечения луча с окружностями и 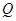проведем линии, параллельные осям координат до пересечения в точке 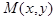. Убедимся, что точка 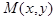принадлежит эллипсу (4). Действительно, из рисунка видно, что

(6)

Подставив значения 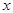и из (6) в (4), убедимся, что они обращают (4) в тождество. Следовательно, точка 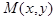лежит на эллипсе.

Уравнения (6) - параметрические уравнения эллипса.

В частности, при , из (6) получаются параметрические уравнения окружности

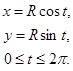(7)

Определение 2. Гиперболой называется множество точек плоскости, для каждой из которых разность расстояний до двух фиксированных точек плоскост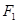и и 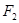, называемых фокусами, есть величина постоянная.

Если точка 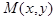лежит на гиперболе, то согласно определению

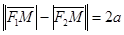(8)

где - некоторый параметр.

Систему координат выберем так же, как в предыдущем случае. Тогда из равенства (8) получим

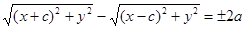. (9)

Уравнение (9) и есть уравнение гиперболы.

После освобождения от иррациональности уравнение (9) примет вид

.

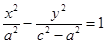Здесь 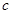- полурасстояние между фокусами.

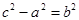Поскольку разность двух сторон треугольника всегда меньше третьей, то . Поэтому обозначим . С учетом этого обозначения уравнение гиперболы примет канонический вид

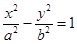. (10)

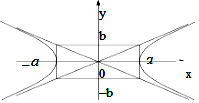
Аналогично предыдущему случаю убедимся, что гипербола является центральной кривой второго порядка.

Из уравнения (10) найдем

. (11)

Из уравнения (11) следует, что , т.е. гипербола расположена вне полосы . Гипербола (10) пересекает ось Оx в точках 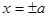и не пересекает ось Оy. Величина называется полуосью гиперболы, а величина - мнимой полуосью гиперболы.

Линии , лежащие на диагоналях прямоугольника со сторонами 2 и 2 , называются асимптотами гиперболы. Эксцентриситет гиперболы

.

Упражнение. Убедиться, что уравнения где , , 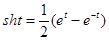, являются параметрическими уравнениями гиперболы.

Опр.3. Параболой называется множество точек плоскости равноудаленных от точки 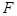, называемой фокусом, и от прямой, называемой директрисой.

Проведем ось ox через фокус 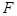перпендикулярно директрисе, а ось oy-через середину отрезка между фокусом и директрисой. Согласно определению

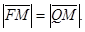(12)

Поскольку то уравнение (12) примет вид (13)

Уравнение (13) и есть уравнение параболы. После упрощения оно примет канонический вид

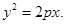(14)

Легко убедиться, что парабола имеет только одну ось симметрии, поэтому она не является центральной кривой второго порядка.

Канонические уравнения эллипса, гиперболы и параболы просты по форме из-за удачного выбора системы координат. Если, например, оси симметрии эллипса параллельны осям координат, но центр симметрии лежит в точке , т.е. не совпадает с началом координат, то уравнение эллипса усложнится и будет следующим

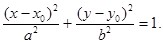
Если оси симметрии не будут параллельны осям координат, то уравнение эллипса еще более усложнится, в нем появится слагаемое, содержащее произведение .

Запишем общее уравнение второго порядка

. (15)

Это уравнение состоит из квадратичной формы 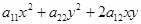, линейной формы и свободного члена .

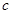Теорема. Уравнение (15) геометрически представляет собой либо эллипс, либо гиперболу, либо параболу и ничего больше, если не считать вырожденные случаи (без доказательства).

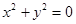Перечислим вырожденные случаи: - пустое множество; - одна точка (0,0); - пара пересекающихся прямых.

Дата добавления: 2014-12-27