Решение

При 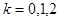получаются корни

,

, .

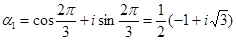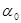При k = 3 что совпадает с . Все последующие корни будут повторяться, так что различных корней будет только три.

Положим по определению для всех вещественных y

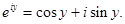(6)

Формула (6) называется формулой Эйлера, 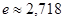– иррациональное число, основание натурального логарифма. Используя формулу Эйлера и предполагая верными обычные правила действия со степенями, найдем

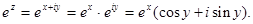(7)

Замечание 1. Формула (7) определяет функцию комплексного переменного z . Функция эта периодическая с периодом .

Действительно,

т.е. .

Используя формулу Эйлера, получим еще одну форму записи комплексного числа- показательную.

(8)

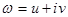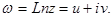Назовем логарифмом числа z комплексное число такое, что Таким образом, Пусть тогда

. (9)

Найдем модуль и аргумент числа .

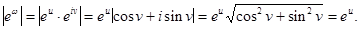
Тогда очевидно 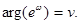Из равенства комплексных чисел (9) получим Следовательно,

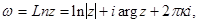
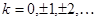. (10)

Замечание 2. Формула (10) определяет функцию комплексного переменного правда, эта функция многозначна, т.к. одному значению аргумента z она ставит в соответствие бесконечное множество значений функции.

Можно убедиться в справедливости обычных правил логарифмирования. В частности , . Однако, в силу многозначности логарифмической функции .

Пример 3. Найти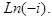

Решение. Согласно формуле (10)

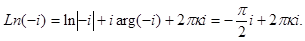
Рассмотрим теперь возвышение комплексного числа в любую комплексную степень. По определению положим

. (11)

Пример 4. Найти

Решение. Согласно формуле (11) и результату примера 3, получим

Пример 5. Найти

Решение.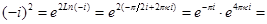

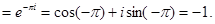
§ 3. Понятие матрицы и определителя. Свойства определителей

Матрицей размера 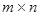называется прямоугольная таблица чисел, содержащая m строк и n столбцов.

.

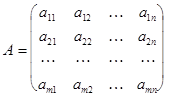Элемент матрицы A, стоящий на пересечении i-ой строки и j-ого столбца обозначают Приведем примеры матриц.

, , , .

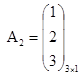Если число строк m равно числу столбцов n матрицы, то она называется квадратной n-ого порядка.

Одной из основных числовых характеристик квадратной матрицы является ее определитель (детерминант). Определителем матрицы второго порядка называется число, определяемое формулой

. (1)

Определители часто используются для решения систем линейных алгебраических уравнений (СЛАУ). Решим систему двух уравнений с двумя неизвестными

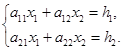
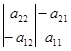
Умножим обе части первого уравнения на , а второго на (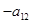) и результаты сложим. Получим 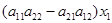= = 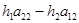или , где

, .

Определитель называется определителем системы, а определитель получается из определителя путем замены первого столбца на столбец свободных членов системы.

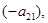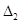Умножив первое уравнение системы на второе на аналогично найдем Определитель получается из определителя путем замены второго столбца на столбец свободных членов. Если то решения системы запишутся в виде

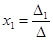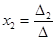, . (2)

Формулы (2) называются формулами Крамера.

Пример. Решить систему

Решение. Вычислим определители , и 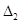по формуле (1):

, , .

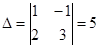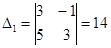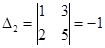Используя формулы Крамера, получим

Определение 1. Минором 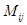элемента матрицы A называют определитель, который получается из определителя матрицы A путем вычеркивания i-ой строки и j-ого столбца. Рассмотрим для примера матрицу третьего порядка и ее некоторые миноры.

, .

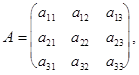
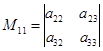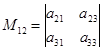Выражение 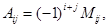называется алгебраическим дополнением элемента .

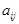Определителем матрицы n-ого порядка назовем число, определяемое формулой

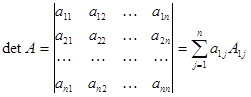. (3)

Формулу (3) называют правилом раскрытия определителя по элементам первой строки. Знак означает суммирование. Для примера раскроем определитель матрицы третьего порядка.

=

= =

= .

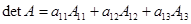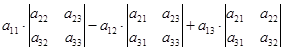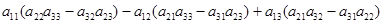Зная теперь, как вычисляются определители третьего порядка, можем вычислить по формуле (3) определитель четвертого порядка и т.д.

Рассмотрим некоторые свойства определителей.

1. Определитель изменит только знак, если поменять местами две его строки (без доказательства).

Проверим это свойство на определителе второго порядка.

.

.

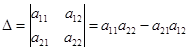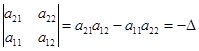Свойство выполняется.

Следствие. Если определитель имеет две одинаковые строки, то он равен нулю.

Доказательство. Поменяем две одинаковые строки, определитель не изменится. Но согласно свойству 1 он должен изменить знак, т.е. должно выполняться равенство, 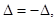что возможно только при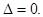

2. (Теорема Лапласа). Определитель можно раскрывать по элементам любой строки (без доказательства).

.

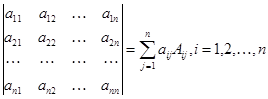Следствие. Если в определителе имеется нулевая строка, то он равен нулю. Доказательство очевидно.

3. Общий множитель любой строки определителя можно вынести за его знак, т.е.

.

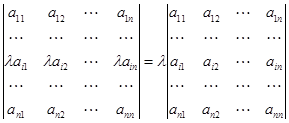Доказательство. Разложить левый и правый определители по элементам i-ой строки. Результаты будут одинаковые.

Следствие. Если определитель имеет пропорциональные строки, то он равен нулю. Доказательство. Вынося коэффициент пропорциональности за знак определителя, получим определитель с двумя одинаковыми строками, который равен нулю.

Дата добавления: 2014-12-27