Уравнения плоскости

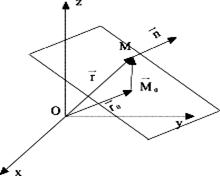
Рассмотрим ортонормиро-ванный базис в пространстве и найдем уравнение плоскости, проходящей через точку 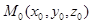перпен-дикулярно вектору Вектор называют нормалью (вектором нормали).

Пусть 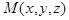– произвольная (текущая) точка плоскости. Тогда вектор =

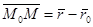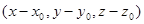= перпендикулярен вектору , следовательно, их скалярное произведение равно нулю

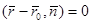. (1)

Уравнение (1) и есть уравнение искомой плоскости в векторном виде. Перепишем его в скалярном виде

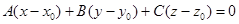, (2)

или , (3)

где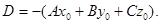

Уравнение (3) называют общим уравнением плоскости.

Если нормаль единичная, т.е. =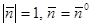

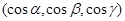= , то уравнение плоскости называют нормальным. Из (1) получим

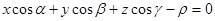, (4)

где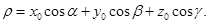

Выясним геометрический смысл величин, входящих в нормальное уравнение плоскости (4). Углы 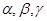– это углы между ортами 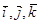и нормалью 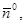направленной от начала координат к плоскости, 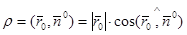– расстояние от начала координат до плоскости.

Пусть произвольная точка, не лежащая в плоскости.

Из рисунка видно, что

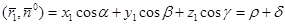
или 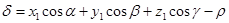. (5)

Величину 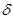называют отклонением точки от плоскости. Отклонение 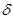может отличаться от расстояния точки от плоскости только знаком. Из (5) видно, чтобы найти отклонение точки от плоскости, достаточно в нормальном уравнении плоскости заменить текущие координаты на координаты точки .

Пример. Написать уравнение плоскости, проходящей через точку перпендикулярно вектору .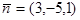

Найти расстояние точки 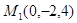от искомой плоскости.

Решение. Воспользуемся уравнением (2). Получим

, (6)

искомое уравнение плоскости. Запишем его в нормальном виде. Чтобы записать общее уравнение плоскости (3) в нормальном виде, достаточно умножить его на нормирующий множитель 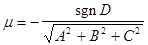, где 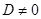. Поскольку в нашем случае D = 4 > 0, то 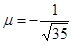. Умножая уравнение (6) на получим нормальное уравнение плоскости

. (7)

Отклонение найдем по формуле (5).

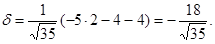Расстояние точки от плоскости очевидно равно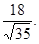

Пусть в общем уравнении (3) все коэффициенты A, B, C и D отличны от нуля. Тогда его можно переписать в виде

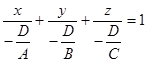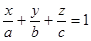или (8)

Уравнение (8) называют уравнением плоскости в отрезках. Легко убедиться, что , , 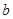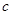– это отрезки на осях координат, отсекаемые плоскостью (убедиться в этом самостоятельно).

Запишем уравнение плоскости, проходящей через три точки , , 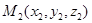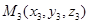. Выберем произвольную точку 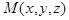на плоскости. Тогда векторы 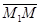, , 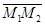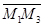будут лежать в этой плоскости. Следовательно, их смешанное произведение равно нулю, т.е.

или 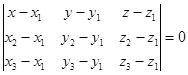. (9)

Уравнение (9) и есть искомое уравнение.

Рассмотрим угол между двумя плоскостями

и 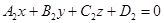. (10)

Т.к. угол между нормалями 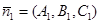, 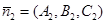и линейный угол двугранного угла между плоскостями равны, то очевидно , (11)

где 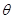-угол между плоскостями.

Из (11) следует условие перпендикулярности двух плоскостей

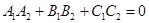. (12)

Если плоскости параллельны, то нормали 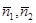коллинеарны, следовательно,

. (13)

Равенство (13) выражает условие параллельности плоскостей.

Запишем теперь уравнение плоскости, проходящей через точку 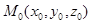параллельно двум неколлинеарным векторам и . Пусть 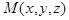произвольная точка плоскости. Тогда векторы и компланарные, следовательно, линейно зависимые, т.е. или

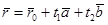. (14)

Здесь некоторые параметры, а уравнение (14) называется векторным параметрическим уравнением плоскости.

Дата добавления: 2014-12-27