Структурный анализ механизма

ХАРЬКОВ 2013

Содержание

1. Структурный анализ механизма…………………………………. 3-7

2. Решение задачи методом замкнутых контуров…..……………. 8-18

3. Решение задачи векторно-графическим методом…………...…19-21

4. Сравнение результатов двух методов……………………………...22

5. Выводы…………………………………………………………….…23

6. Библиографический список…………………………………………24

7. Приложение………………………………………………………….25

Пронумеруем подвижные звенья механизма, начиная с 1. Неподвижные звенья - стойки, обозначим 0. Результат нумерации приведен ниже на рисунке.

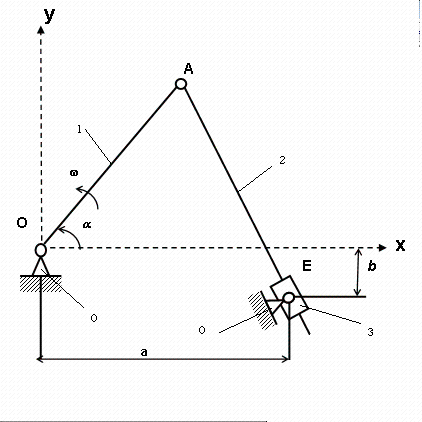
Рисунок 1

Звенья 1, 2 и 3 - подвижные. Число подвижных звеньев n равно

n:=3:

Звенья, обозначенные 0 - стойки. Число стоек равно 2.

Перечисляем низшие кинематические пары (НКП), присутствующие в механизме:

0-1, НКП, V класс, вращательная;

1-2, НКП, V класс, вращательная;

2-3, НКП, V класс, поступательная;

3-0, НКП, V класс, вращательная.

Число НКП V класса p₅ равно

p5:=4:

НКП IV класса в данном механизме отсутствуют. Следовательно их число p₄ равно p4:=0:

Находим степень подвижности механизма W по формуле Чебышева

W:=3*n-2*p5-p4

Полученное значение подвижности W =1 означает, что в нашем механизме можно задать одно ведущее звено.

Имеется два варианта выбора ведушего звена.

В качестве ведущего звена выбираем звено 1, совершающее вращательное движение. Обычно это звено называт кривошипом.

Ведущее звено и стойка образуют так называемый основной механизм. Выделяем основной механизм, образованный стойкой 0 и звеном 1. Ниже на рисунке показан основной механизм.

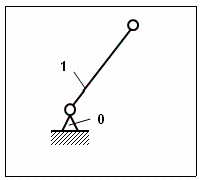
Рисунок 2

В нашем случаи имеется одна группа Ассура. Ее образуют звенья 2 и 3.

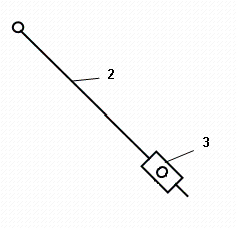
Рисунок 3

Группа Ассура, образованная звеньями 2 и 3, относится к II класу 2-го порядка 3-го вида (к механизму подсоединяется через вращательную и поступательную кинематические пары).

Докажем, что выбранная группа звеньев 2 и 3 образуют группу Ассура.

Присоединяем выбранную группу звеньев к стойкам.Это подсоединение приведено на рисунке.

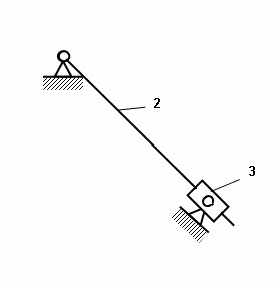
Рисунок 4

Результат нумерации показан на рис. 4.

Находим число подвижных звеньев

n_гр:=2:

Перечисляем кинематические пары:

0-2, НКП, V класс, вращательная;

2-3, НКП, V класс, поступательная;

3-0, НКП, V класс, вращательная.

Число НКП V класса равно

p5_гр:=3:

Число НКП IV класса равно

p4_гр:=0:

Степень подвижности механизма равна

W_гр:=3*n_гр-2*p5_гр-p4_гр

Итак, подвижность полученного механизма равна 0. Что и требовалось доказать.

В группе Ассура выделяем следующие характерные точки, которые приведены на рисунке.

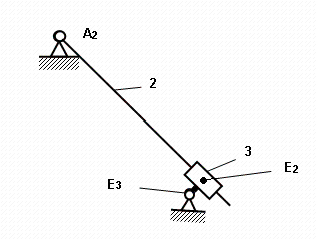
Рисунок 5

Перечисляем характерные точки:

- первая крайняя точка A₁ (A);

- средняя точка E₂;

- вторая крайняя точка E₃.

Крайняя точка A₂ и E₂ принадлежат одному звену 2.

Крайняя точка E₃ принадлежит звену 3.

Анализ движений звеньев показывает:

- звено 1 (кривошип) равномерно вращается вокруг оси, проходящей через точку О перпендикулярно к плоскости механизма;

- звено 2 (шатун) совершает плоское движение в плоскости механизма;

- ползун 3 движется поступательно в плоскости механизма.

РЕШЕНИЕ ЗАДАЧИ МЕТОДОМ ЗАМКНУТЫХ КОНТУРОВ

Представим механизм в виде замкнутого векторного многоугольника (см. чертеж):

y

a b

α x

d

c β

Запишем условие замкнутости контура:

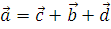
Спроецируем векторные тождества на оси координат:

Oy: b sin β = a sin 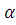- d
Ox:

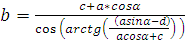
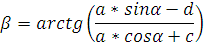
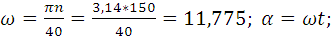- n – количество оборотов звена в минуту

Далее, ввиду сложности полученных функций, воспользуемся математической средой MATLAB 14, для определения законов изменения скорости и ускорения, и построения графиков.

Момент времени, соответствующий заданному условием положению рычажного механизма. Назовем этот момент времени t0.

Вектор AE заданный функцией зависимости от времени.

Общий вид графика изменения вектора АE от времени

График изменения вектора АE в увеличенном масштабе

Вычисление длины вектора АE1 в момент времени t0.

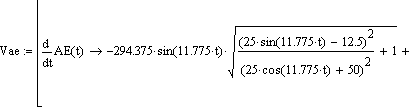
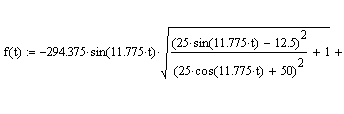
Общий вид графика изменения Vae от времени

График изменения вектора Vae в увеличенном масштабе

Из данного графика можно узнать длину вектора Vae в любой момент времени.

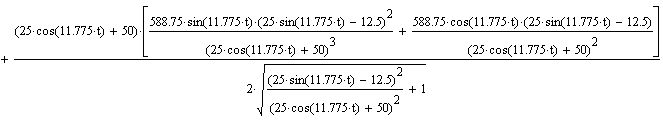
Нахождение ускорения Wae путем дифференцирования вектора Vae по времени.

Вычисление Vae в момент времени t0.

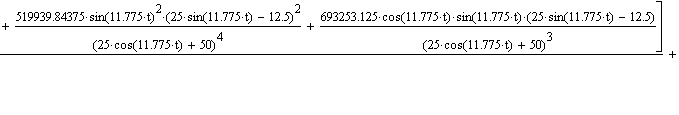
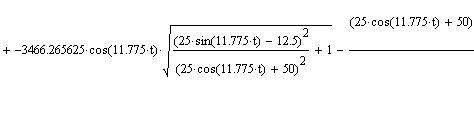
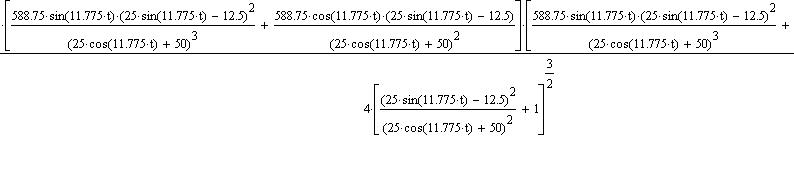
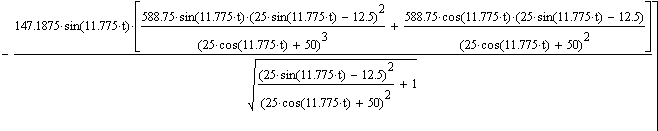
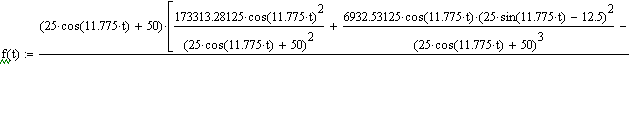
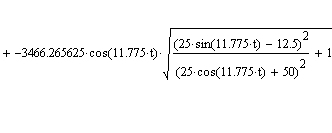
Общий вид графика изменения Wae от времени

График изменения вектора Wae в увеличенном масштабе

Из данного графика можно узнать длину вектора Wae в любой момент времени.

Вычисление длины вектора Wae в момент времени t0.

Угол beta заданный функцией зависимости от времени.

Общий вид графика изменения угла beta от времени

График изменения угла beta в увеличенном масштабе

Вычисление длины угла beta в момент времени t0.

Нахождение угловой скорости wbeta путем дифференцирования beta по времени.

Общий вид графика изменения wbeta от времени

График изменения вектора wbeta в увеличенном масштабе

Из данного графика можно узнать длину вектора Voa в любой момент времени.

Вычисление длины вектора Voa в момент времени t0.

Нахождение углового ускорения ebeta путем дифференцирования угловой скорости wbeta по времени.

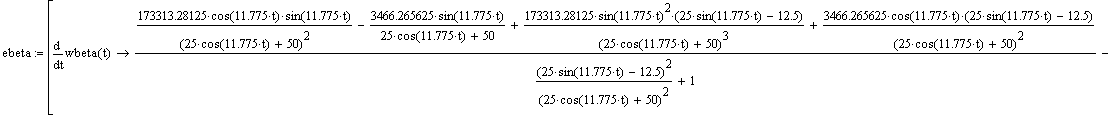
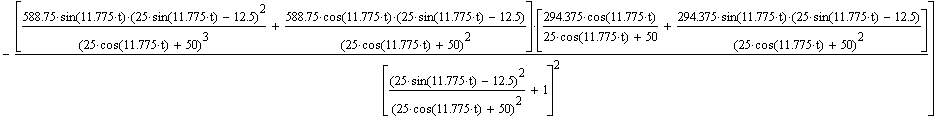
Общий вид графика изменения ebeta от времени

График изменения вектора ebeta в увеличенном масштабе

Из данного графика можно узнать угловое ускорение ebeta в любой момент времени.

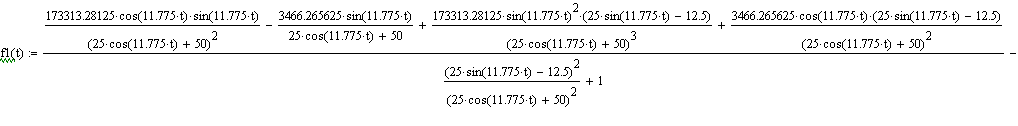
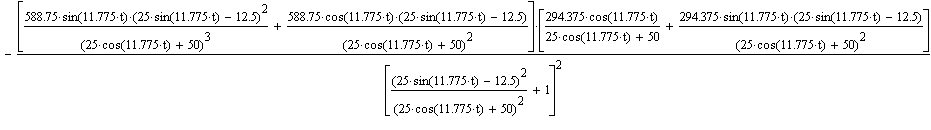
Вычисление углового ускорения ebeta в момент времени t0.

РЕШЕНИЕ ЗАДАЧИ ВЕКТОРНО-ГРАФИЧЕСКИМ МЕТОДОМ

Найдем скорость движения точки E₂:

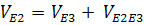
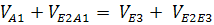
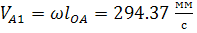(перпендикулярно ОА)

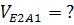(параллельно АЕ)

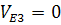(в полюсе)

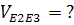(параллельно АЕ)

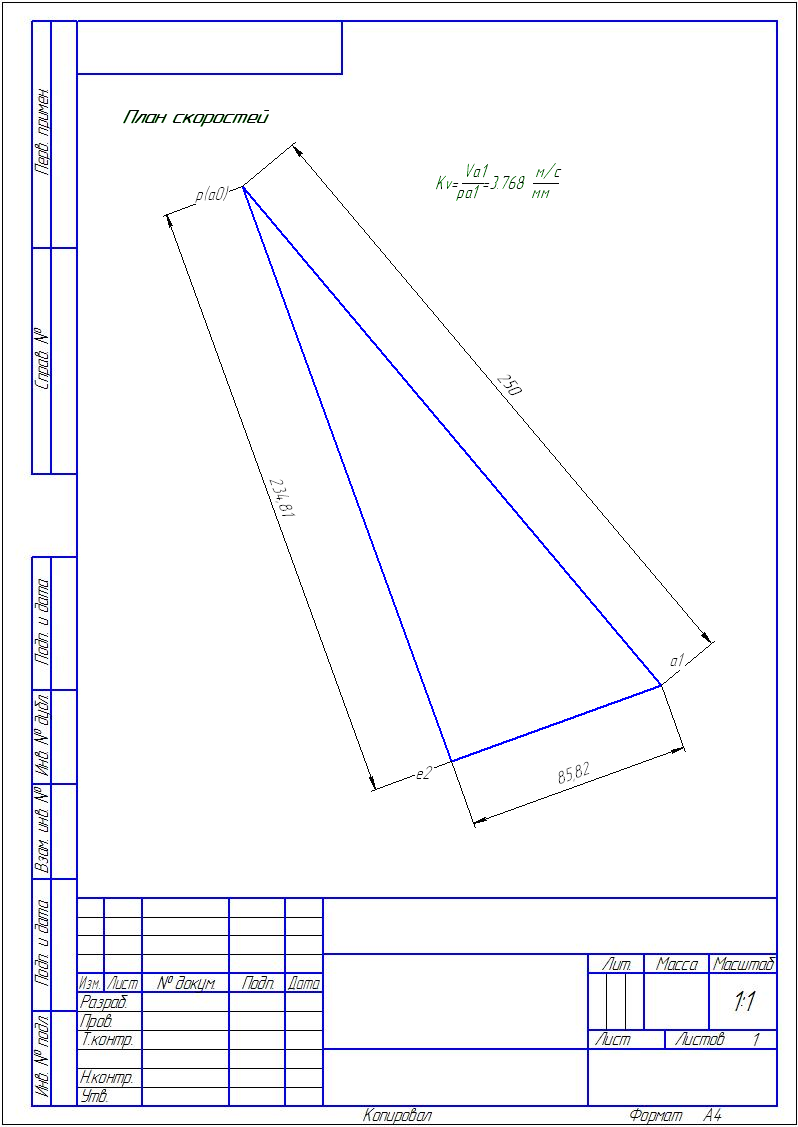
Решаем полученное уравнение с помощью плана скоростей (см. чертеж).

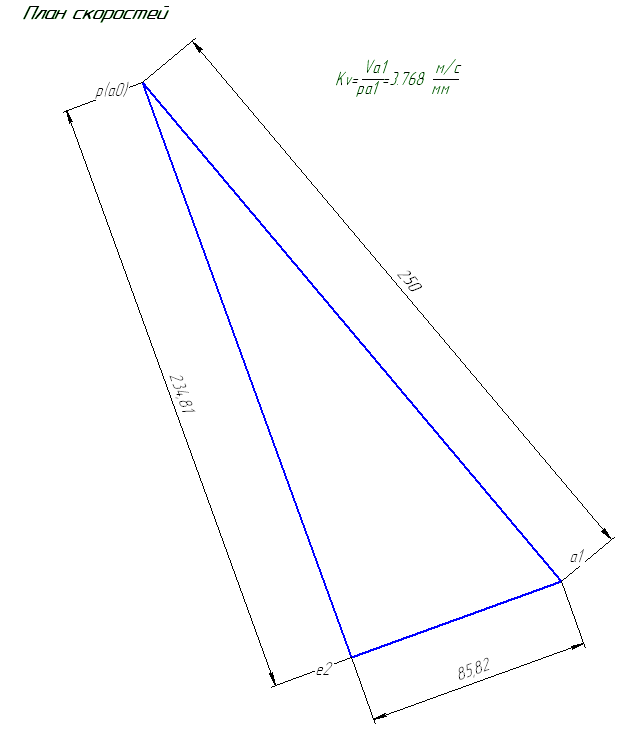
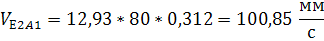
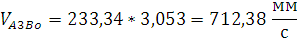
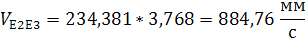
Найдем ускорение точки :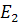

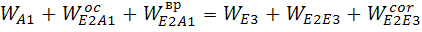
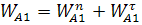
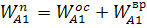
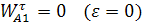
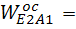w²₂L_AB = 12.93*12.93*25=4181.17 (напр. от Е к А)

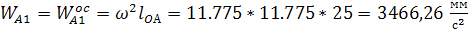(параллельно АО);

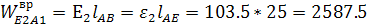(перпендикулярно АВ);

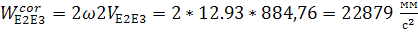(перпендикулярно ОА);

(в полюсе);

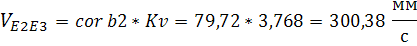
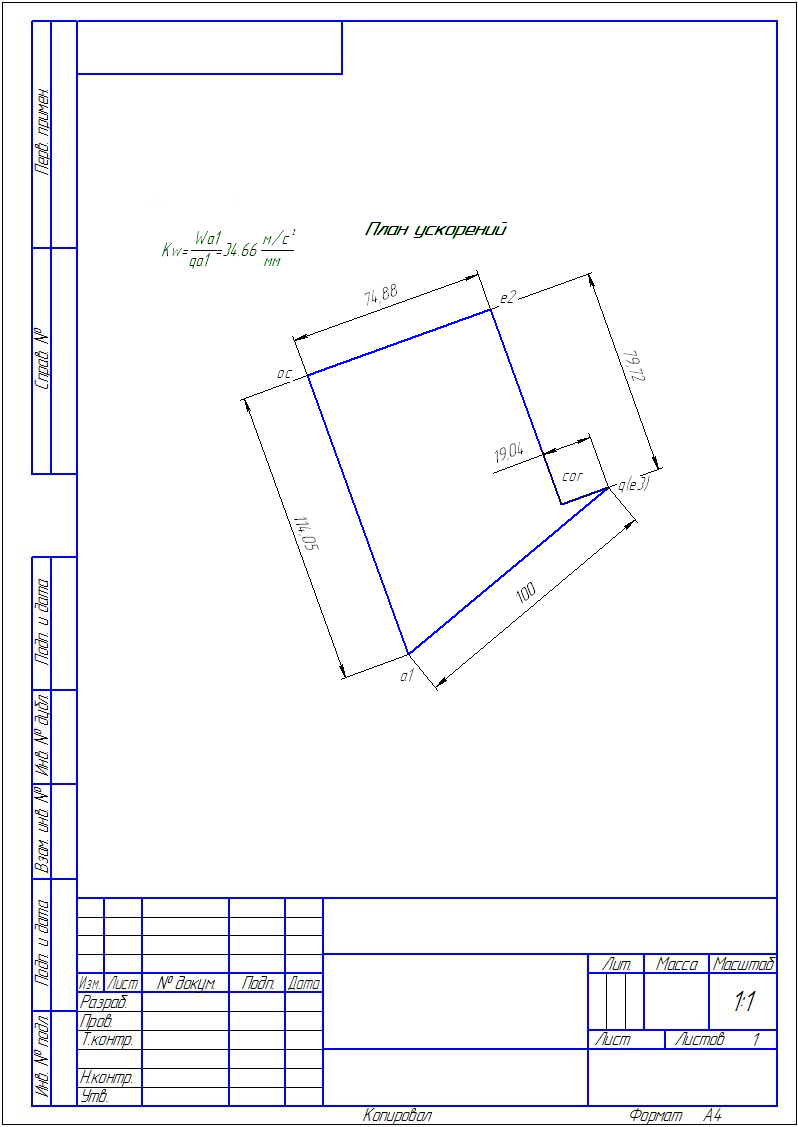
Решаем полученное уравнение с помощью плана ускорений (см. чертеж).

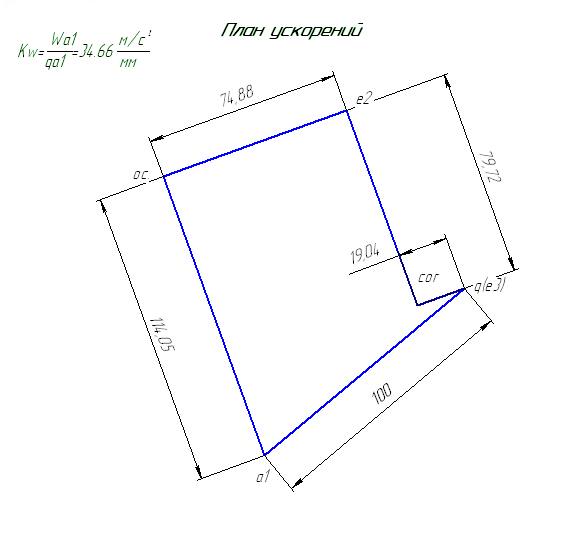
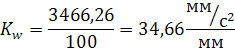
4 СРАВНЕНИЕ РЕЗУЛЬТАТОВ ДВУХ МЕТОДОВ

Погрешность в процентах результата, полученного векторно-графическим методом, определяем по формуле

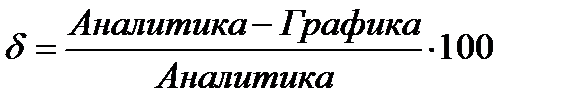. (4.1)

	Метод замкнутых контуров	Векторно-графический метод	Погрешность
VА1, мм/ с	294.37	294.37
VЕ2А1, мм/ с	100.85	100.85
ω рад/с	11.775	11.775
WE2A1 мм/с^2	2587.5	2587.5
WA1 мм/с^2	3466.26	3466.26
ε2 рад/сек

В табл.4.1 приведены результаты сравнения.

Таблица 4.1

ВЫВОДЫ

1. Аналитический метод позволяет получить информацию о движении исследуемого звена в пределах всего полного цикла работы механизма, при этом машинное решение задачи дает возможность получить информацию для любого числа положений механизма в пределах этого цикла и с высокой степенью точности. В качестве входных параметров этой модели приняты:

- закон движения ведущего звена;

- размеры звеньев;

- начальное положение основного звена;

Выходными параметрами этой модели являются временные зависимости кинематических величин, характеризующих движение механизма. Получение этих зависимостей позволяет проводить различные исследования движения механизма.

2. Трудность применения аналитического метода обусловлена способом решения разрешающей системы уравнений. Но при наличие соответствующего программного обеспечения эта трудность несущественна.

3. Векторно-графический метод позволяет получить решение только для одного положения механизма. В этом состоит его основной недостаток.

4. Простота и наглядность получения решения являются преимуществами векторно-графического метода. При применении соответствующих программ автоматизированного проектирования точность решения, получаемого данным методом, вполне достаточная.

5. Сравнение результатов, полученных двумя методами кинематического исследования, показало их совпадение. В первую очередь это связано с тем, что планы скоростей и ускорений нами строились программой КОМПАС.

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1. «Кинематический анализ приборных механизмов». Ю.И.Добежа, Н.Д.Кошевой. г.Харьков «ХАИ», 1985г.

2. «Краткий курс теоретической механики». С.М. Тарг. г.Москва, 1974г.

3. Конспект лекций по курсу «Техническая механика. Кинематика».

ПРИЛОЖЕНИЕ

ПЛАН ПОЛОЖЕНИЯ, СКОРОСТЕЙ МЕХАНИЗМА

ПЛАН ПОЛОЖЕНИЯ, УСКОРЕНИЙ МЕХАНИЗМА

% Номер кинематической схемы........................................

N_shema=15;

% Вариант данных....................................................

N_data=1;

% Геометрические размеры (задают в мм)...............................

A=25;

% Частота вращения ведущего звена (задают в об/мин).................

n1=150;

pi=3.14;

% 2.2 Проекции векторного уравнения замкнутого контура на координатные оси ось x

eq1='a*sin(alpha+omega1*t)-d';

% ось y

eq2='a*cos(alpha+omega1*t)+c*sin(betta)';

% 2.3 Решение системы 2-х уравнений

syms betta b c t OE omega1 alpha

a=sym('sqrt(b^2-c^2*(sin(alpha+omega1*t))^2)-c*cos(alpha+omega1*t)');

beta=sym('atan((a*sin(alpha)-d)/(a*cos(alpha)+c))');

disp('Параметр a --->');disp(a);

disp('');

disp('Параметр beta --->');disp(beta);

disp(' ');

% 2.4 Закон движения ведущего звена 1

T1=60/n1;

disp(['Время одного оборота ведущего звена T1, с --> ', num2str(T1)]);

omega1=sym(pi*n1/40);

% Функция времени угла поворота beta(t) ведущего звена

beta=sym(atan((25*sin(11.775*t)-12/5)/(25*cos(11.775*t)+50));

disp('Функция времени угла поворота ведущего звена --->');

disp(alpha);

% задание начального положения ведущего звена в рад

alpha=subs(alpha,'alpha',pi/4);

omega3=diff(beta,t);

disp('Угловая скорость Omega3 --->');

disp(omega3);

eps3=diff(omega3,t);

disp('Угловое ускорение Epsilon3 --->');

disp(eps3);

VE2E1=diff(a,t);

disp('Скорость VE2E1 --->');

disp(VE2E1);

WE2E1=diff(VE2E1,t);

disp('Ускорение WE2E1 --->');

disp(WE2E1);

alpha0=0;

figure

subplot(3,1,1);

beta=subs(beta,'omega1',pi*n1/30);

beta=subs(beta,'b',BE);

beta=subs(beta,'c',OB);

beta=subs(beta,'alpha0',0)

ezplot(inline(180/pi*betta-'z'),[0 1.1*T1 -4 184])

title '\beta=\beta(t)';

xlabel 't, с';

ylabel '\beta, град';

subplot(3,1,2);

omega3=subs(omega3,'b',BE);

omega3=subs(omega3,'c',OB);

omega3=subs(omega3,'alpha',pi/4);

omega3=subs(omega3,'omega1',pi*n1/30);

plot([0 T1],[omega3 omega3]);

title '\omega3=\omega3(t)';

xlabel 't, с';

ylabel '\omega3, рад/с'

subplot(3,1,3);

eps3=subs(eps3,'omega1',pi*n1/30);

eps3=subs(eps3,'b',BE);

eps3=subs(eps3,'c',OB);

eps3=subs(eps3,'alpha',pi/4);

plot([0 T1],[eps3 eps3]);

title '\epsilon3=\epsilon3(t)';

xlabel 't, с';

ylabel '\epsilon3, рад/с^2'

% 2.5.8 Графики кинематических величин движения звена 2

figure

subplot(3,1,1);

a=subs(a,'omega1',pi*n1/30);

a=subs(a,'b',BE);

a=subs(a,'c',OB);

a=subs(a,'alpha',pi/4);

ezplot(inline(a-'z'),[0 T1 0 160]);

title 'a=a(t)';

xlabel 't, с';

ylabel 'a, мм';

subplot(3,1,2);

VE2E1=subs(VE2E1,'omega1',pi*n1/30);

VE2E1=subs(VE2E1,'b',BE);

VE2E1=subs(VE2E1,'c',OB);

VE2E1=subs(VE2E1,'alpha',pi/4);

ezplot(inline(VE2E1-'z'),[0 T1 -800 800]);

title 'VE2E1=VE2E1(t)';

xlabel 't, с'

ylabel 'VE2E1, мм/c';

subplot(3,1,3);

WE2E1=subs(WE2E1,'omega1',pi*n1/30);

WE2E1=subs(WE2E1,'b',BE);

WE2E1=subs(WE2E1,'c',OB);

WE2E1=subs(WE2E1,'alpha',pi/4);

ezplot(inline(WE2E1-'z'),[0 T1 -7000 500]);

title 'WE2E1=WE2E1(t)';

xlabel 't, с';

ylabel 'WE2E1, мм/c^2';

Alpha=40;

disp('Заданный угол положения ведущего звена 1 - угол Alpha, в град --->');

disp(Alpha);

% Находим момент времени t, когда ведущее звено 1 составит с осью x

% угол Alpha

Alpha=Alpha*pi/180;

fx=sym(alpha-Alpha);

r=solve(fx,t);r=0.0978;

disp('Момент времени t в сек --->');

disp(r);

OE=a;

% 2.6.2 Модули скорости и ускорения точки E звена 1

omega1=sym(pi*n1/30)

VE=abs(subs(omega1,t,r)*OE);

WEn=abs((subs(omega1,t,r))^2*OE);

WE=WEn;

disp('Модуль скорости точки E - VE, в мм/с --->'); disp(VE);

disp('Модуль ускорения точки E - WE, в мм/с^2 --->'); disp(WE)

BE=sqrt(OE^2+OB^2-2*OE*OB*cos(pi/2+Alpha));

VBE=abs(subs(omega3,t,r))*BE;

WBEn=sym(subs(omega3,t,r))^2*BE;

WBEt=(subs(eps3,t,r))*BE;

disp('Модуль VBE,в мм/с --->'); disp(eval(VBE));

disp('Модуль ускорения WBEn, в мм/с^2 --->'); disp(eval(WBEn));

disp('Модуль ускорения WBEt, в мм/с^2 --->'); disp(eval(WBEt));

% 2.6.3 Угловая скорость и угловое ускорение звена 3

disp('Угловая скорость звена 3 - omega3,в рад/с --->');

disp(eval(subs(omega3,t,r)));

disp('Угловое ускорение звена 3 - epsilon3,в рад/с^2 --->');

disp(eval(subs(eps3,t,r)));

% 2.6.4 Модули скорости и ускорения точки E звена 3

Wc=2*abs(subs(omega1,t,r)*subs(VE2E1,t,r));

VBE=abs(subs(VBE,t,r));

disp('Модуль скорости точки В - VBE,в мм/с --->'); disp(VBE);

disp('Модуль кориолисова ускорения - Wc,в мм/с^2 --->'); disp(Wc);

t=0.3;

% длины отрезков pa, ab и pb в мм

pa=50;ab=50;pb=70.11;

VE2=omega1*a;

% коэффициент масщтаба kv плана скоростей в (мм/(с*мм))

kv=VE2/pa;

% скорости VE3E2 и VE3B3

VE3E2=kv*ab;

VE3B3=kv*pb;

disp(' ПЛАН СКОРОСТЕЙ')

disp('Масштабный коэффициент kv, мм/(с*мм) --->'); disp(kv);

disp('Модуль скорости точки E2 - VE2, в мм/с --->'); disp(kv*pa);

disp('Модуль скорости точки E3E2 - VE3E2, в мм/с --->'); disp(VE3E2);

disp('Модуль скорости точки E3B3 - VE3B3, в мм/с --->'); disp(VE3B3);

disp('Углая скорость звена 3 - Omega3, в рад/с ---> ');disp(VE3B3/BE);

disp('Omega3 направлена ---> против хода часовой стрелки');

qa=50;ac=22.8825;cb=27.63;be=0;qb=31.65;

WE2=(omega1)^2*a;

WE3B3n=(omega3)^2*BE;

% коэффициент масщтаба kw плана ускорений в (мм/(с^2*мм))

kw=WE2/qa;

WE3B3t=kw*cb;

WE3E2=kw*be;

disp(' ПЛАН УСКОРЕНИЙ')

disp('Масштабный коэффициент kw, мм/(с^2*мм) --->');disp(kw);

disp('Модуль ускорения точки E2 - WE2, в мм/с^2 --->'); disp(kw*qa);

disp('Модуль ускорения точки E3n - WE3B3n, в мм/с^2 --->'); disp(kw*qb);

disp('Модуль ускорения точки E3t - WE3B3t, в мм/с^2 --->'); disp(WE3B3t);

disp('Модуль кориолисова ускорения - Wс, в мм/с^2 --->'); disp(kw*ac);

disp('Модуль ускорения точки E3E2 - WE3E2, в мм/с^2 --->'); disp(WE3E2);

disp('Угловое ускорение звена 3 - Epsilon3, в рад/с^2 ---> ');

disp(WE3B3t/BE);

disp('Epsilon3 направлена ---> против хода часовой стрелки');

% 4.1 Скорость VE2E1 в мм/с

delta_VE2E1=((abs(VE2E1)-VE3E2)/abs(VE2E1))*100;

% 4.2 Скорость VE в мм/с

delta_VE=((VE-VE2)/VE)*100;

% 4.3 Угловая скорость Omega3 в рад/с

absOmega3=abs(subs(omega3,t,r));

delta_Omega3=((absOmega3-VE3B3/BE)/absOmega3)*100;

% 4.4 Ускорение WBEt в мм/с^2

delta_WBEt=(abs(WE3B3t)-WBEt);

% 4.5 Ускорение WBEn в мм/с^2

delta_WBEn=((abs(WE3B3n)-WBEn)/abs(WE3B3n))*100;

% 4.6 Cкорость VBE в мм/с

delta_VBE=((abs(VE3B3)-VBE)/abs(VE3B3))*100;

% 4.7 Угловое ускорение Epsilon3 в рад/с^2

absEpsilon3=abs(subs(eps3,t,r));

delta_Epsilon3=((WE3B3t/BE-absEpsilon3)/WE3B3t/BE)*100;

% 4.8 Ускорение WEn в мм/с^2

delta_WE=((abs(WE2)-WE)/abs(WE2)*100);

% 4.9 Ускорение WE2E1 в мм/с^2

delta_WE2E1=((abs(WE2E1)-WE3E2)/abs(WE2E1)*100);

disp(' СРАВНЕНИЕ РЕЗУЛЬТАТОВ ДВУХ МЕТОДОВ')

disp('Параметр Аналитика Графика Погрешность');

out1=eval(VE2E1);out2=eval(sym(VE3E2));out3=eval(delta_VE2E1);

disp(['VE2E1,мм/с ',num2str(out1),' ',num2str(out2),...

' ',num2str(out3)]);

out1=eval(VE);out2=eval(sym(VE2));out3=eval(delta_VE);

disp(['VE,мм/с ',...

num2str(out1),' ',num2str(out2),' ',...

num2str(out3)]);

out1=eval(absOmega3);out2=eval(sym(VE3B3/BE));out3=eval(delta_Omega3);

disp(['Omega3,рад/с ',num2str(out1),' ',...

num2str(out2),' ',num2str(out3)]);

out1=eval(WBEt);out2=eval(sym(WE3B3t));out3=eval(delta_WBEt);

disp(['WBEt,мм/с^2 ',num2str(out1),' ',...

num2str(out2),' ',num2str(out3)]);

out1=eval(subs(abs(WE3B3n),t,r));

out2=eval(sym(WBEn));

out3=eval(subs(delta_WBEn,t,r));

disp(['WBEn,мм/с^2 ',num2str(out1),' ',...

num2str(out2),' ',num2str(out3)]);

out1=eval(VBE); out2=eval(VE3B3);

out3=eval(delta_VBE);

disp(['VBE,мм/с ',num2str(out1),' ',...

num2str(out2),' ',num2str(out3)]);

out1=eval(subs(eps3,t,r));out2=eval(sym(WE3B3t/BE));

out3=eval(delta_Epsilon3);

disp(['Epsilon3,рад/с^2 ',num2str(out1),' ',...

num2str(out2),' ',num2str(out3)]);

out1=eval(subs(abs(WE2),t,r));

out2=eval(sym(WE));

out3=eval(subs(delta_WE,t,r));

disp(['WE,мм/с^2 ',num2str(out1),' ',...

num2str(out2),' ',num2str(out3)]);

out1=eval(subs(abs(WE2E1),t,r));

out2=eval(sym(WE3E2));

out3=eval(subs(delta_WE2E1,t,r));

disp(['WE2E1,мм/с^2 ',num2str(out1),' ',...

num2str(out2),' ',num2str(out3)]);

Дата добавления: 2014-12-27