Изображение многогранников

Пересечение треугольников, видимость сторон, определение натуральной величины

--------------------------------------------------------------------------------------------------------------------

6. Какое взаимное положение могут занимать две плоскости?

Таблица 8. Данные треугольника АВС к заданию 7

(координаты и размеры, мм)

№ вар.	ХА	УА	ZА	ХВ	УВ	ZВ	ХС	УС	ZС

-38-

Пересечение треугольников, видимость сторон, определение натуральной величины

------------------------------------------------------------------------------------------------------------------------

Данные треугольника АВС к заданию 7

(координаты и размеры, мм)

Продолжение табл. 8

№ вар.	ХА	УА	ZА	ХВ	УВ	ZВ	ХС	УС	ZС

-39-

Пересечение треугольников, видимость сторон, определение натуральной величины

------------------------------------------------------------------------------------------------------------------------

Данные треугольника DЕК к заданию 7

(координаты и размеры, мм)

Продолжение табл. 8

№ вар.	ХD	УD	ZD	ХЕ	УЕ	ZЕ	ХК	УК	ZК

-40-

Пересечение треугольников, видимость сторон, определение натуральной величины

------------------------------------------------------------------------------------------------------------------------

Данные треугольника DЕК к заданию 7

(координаты и размеры, мм)

Продолжение табл. 8

№ вар.	ХD	УD	ZD	ХЕ	УЕ	ZЕ	ХК	УК	ZК

-41-

Пересечение треугольников, видимость сторон, определение натуральной величины

------------------------------------------------------------------------------------------------------------------------

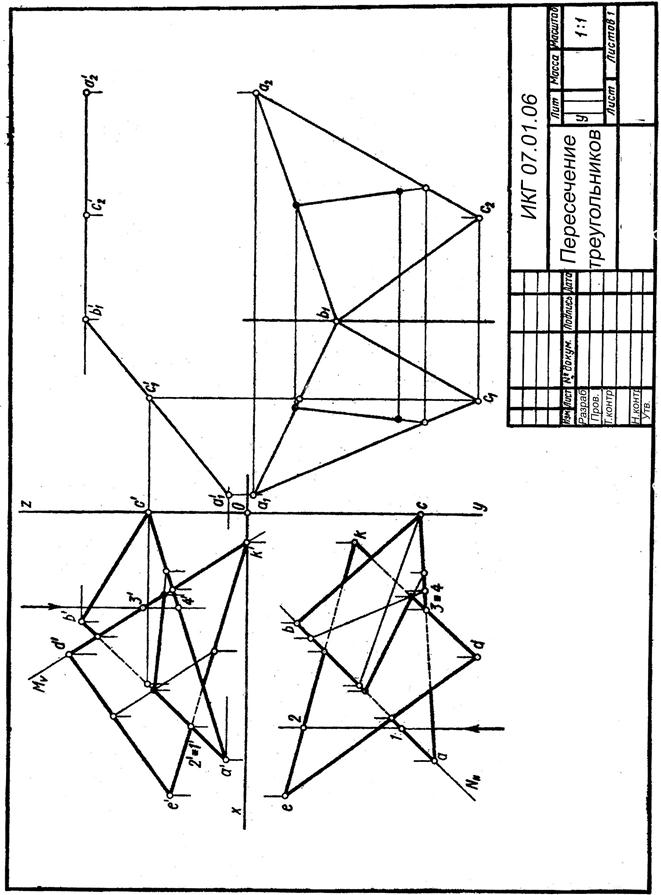
Рис.10. Пример выполнения задания 7.

-42-

Раздел 4. МНОГОГРАННИКИ

На комплексном чертеже многогранники изображаются проекциями своих вершин и ребер, при этом невидимые ребра изображают штриховыми линиями. Кроме этого, рекомендуется отмечать проекции вершин многогранника.

Сечение многогранника плоскостью, является многоугольник, вершинами которого служат точки пересечения ребер многогранника с секущей плоскостью, а сторонами – отрезки прямых пересечения граней многогранника с той же плоскостью.

Поэтому построение сечения многогранника плоскостью сводится к многократному решению задачи о пересечении прямой с плоскостью или же к многократному решению задачи о пересечении двух плоскостей. После построения вершин сечения следует соединить отрезками прямых каждые две вершины, лежащие в одной и той же грани многогранника.

Для определения взаимного положения прямой и поверхности многогранника, нужно провести через эту прямую проецирующую плоскость и по полученной на его поверхности в результате сечения плоскости и многогранника вспомогательной ломаной линии и прямой находят точки пересечения.

Линия пересечения двух многогранников, называется линией перехода, представляет собой некоторую пространственную ломаную линию, которая может разделиться на две и более отдельные части. Эти части могут быть, в частности и плоскими многоугольниками.

Поэтому построение линий пересечения многогранников сводится к многократному решению задачи о пересечении прямой с плоскостью, а построение сторон этой линии к многократному решению задачи о пересечении двух плоскостей. Обычно предпочитают находить вершины линии пересечения, а ее стороны находят соединением соответствующих вершин. При этом очевидно, что только те пары вершин можно соединять отрезками прямых, которые лежат в одной и той же грани первого многогранника и в то же время, в одной и той же грани второго многогранника. Если же рассматриваемая пара вершин хотя бы в одном многограннике принадлежит разным граням, то такие вершины не соединяются.

При построении линии пересечения надо иметь в виду, что проекции линии пересечения могут располагаться только в пределах плоскости наложения одноименных проекций обоих многогранников.

Дата добавления: 2015-03-29