Теорема 7.2. Абсолютная погрешность алгебраической суммы нескольких приближённых чисел не превышает суммы абсолютных погрешностей слагаемых

Погрешности арифметических действий

.

Теорема 7.1. Если положительное приближённое число имеет верных десятичных знаков, то относительная погрешность этого числа не превосходит величины

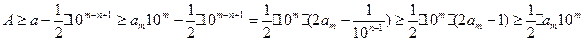Доказательство. По определению, . Значит, и

, что и требовалось доказать.

С помощью этого утверждения можно решать, например, такие задачи.

Задача: оценить относительную погрешность замены числа 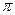числом .

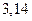Решение: , поэтому . (На самом деле в этом примере можно дать и более точную оценку, так как мы знаем, что и ).

Задача: сколько десятичных знаков числа 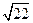следует взять, чтобы относительная погрешность вычисления не превышала .

Решение: Первая цифра этого числа, очевидно, равна 4. Для того, чтобы выполнялась оценка , достаточно взять .

Доказательство. Пусть - точные значения, - приближающие их числа. Тогда

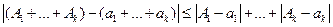, по свойству 2 абсолютной величины, что и требовалось доказать.

Это утверждение означает, что . Поэтому обычно правую часть этого неравенства и принимают за оценку абсолютной погрешности суммы. Таким образом, абсолютная погрешность суммы оказывается не меньше, чем наибольшая из абсолютных погрешностей слагаемых. Следовательно, не имеет смысла сохранять излишние знаки и в более точных слагаемых.

Итак, при сложении приближённых чисел используется такое простое правило. Во-первых, следует найти числа, десятичная запись которых содержит наименьшее количество знаков после запятой. Остальные числа округлить так же, как найденные выше, взяв ещё один лишний знак. Произвести сложение полученных округлённых чисел и округлить результат.

Сложим, для примера, числа 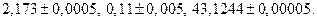Ясно, что точность вычисления определяется вторым слагаемым. Поэтому, в соответствии с выписанным выше правилом, сохраним первое и второе числа и округлим третье следующим образом: . Тогда первое и третье слагаемые дадут в сумме . Добавление второго слагаемого приведёт к 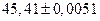. Из этого следует, что верными цифрами суммы будут первые три её цифры.

Дата добавления: 2015-04-24