Теорема 7.4. Относительная погрешность произведения нескольких положительных приближённых чисел не превышает суммы их относительных погрешностей

Теорема 7.3. Относительная погрешность суммы слагаемых одного и того же знака не превышает наибольшей относительной погрешности.

Доказательство. Пусть, как и выше, точные числа равны , приближённые числа равны , абсолютные погрешности оценены числами , относительные погрешности равны и наибольшая из них есть . Тогда относительная погрешность суммы не превосходит числа .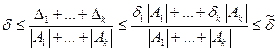

Перейдём к погрешности произведения.

Доказательство. Пусть, в прежних обозначениях 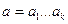. Тогда . Мы сейчас воспользуемся правилом, которое будет доказано позже. Согласно этому правилу, для погрешностей выполняется равенство: . Из этого равенства вытекает также приближённое равенство: , откуда, в свою очередь, 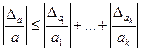, что и требовалось доказать.

Пример. Найдём произведение приближённых чисел . Оценкой сверху для относительной погрешности служит число . Произведение приблизительно равно и абсолютная погрешность не превосходит 1,45. Поэтому произведение имеет два верных знака и его следует записать так: .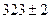

Полезно руководствоваться таким правилом. Пусть мы ищем произведение нескольких приближённых сомножителей. Тогда, во-первых, округлим все сомножители, кроме наименее точного, так, чтобы они имели на одну значащую цифру больше, чем число верных цифр в этом наименее точном из сомножителей. В результате умножения сохранить столько значащих цифр, сколько верных цифр в наименее точном из сомножителей.

Как определить число верных знаков произведения? Рассмотрим

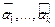сомножителей , каждый из которых пусть имеет верных цифр. Пусть - их первые значащие цифры. Тогда, как доказано выше, , и по предыдущему утверждению, 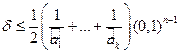. Поскольку, по условию, и все . Поэтому 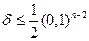. Следовательно, число верных знаков может уменьшиться не более, чем на 2. Если сомножители имеют разное количество верных цифр, то под числом следует понимать наименьшее из чисел верных знаков сомножителей.

Вопрос о погрешности частного решается примерно так же, как и в случае произведения. Именно, если 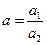, то и, следовательно,

Дата добавления: 2015-04-24