Вторая производная функции , заданной параметрически

Теорема 21.2.(Г. Лейбниц). Если функции f и g на некотором промежутке имеют производные функции f(n) и g(n), n, то существует (fg)(n) и

(fg)⁽ⁿ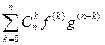⁾ = = fg⁽ⁿ⁾ + nf´g^(n-1) + … + f^(k)g^(n-k) + … + nf^(n-1)g´ + f⁽ⁿ⁾g. (1)

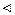Для n=1 утверждение справедливо по теореме 19.8: вместе с f и g произведение fg также дифференцируемо и

(fg)´ = fg´ + f´g = C 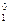f⁽⁰⁾g⁽¹⁾ + C 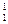f⁽¹⁾g⁽⁰⁾.

Пусть утверждение теоремы справедливо для n, а функции f и g (n+1)-кратно дифференцируемы на рассматриваемом промежутке. Тогда эти функции вместе со своим произведением n-кратно дифференцируемы, и для него справедлива формула (1). Так как в каждом члене правой части этой формулы функции f^(k) и g^(n-k) дифференцируемы, то по теоремам 19.7, 19.8 функция (fg)⁽ⁿ⁾ дифференцируема, причем (fg)⁽ⁿ⁺¹⁾ = ((fg)⁽ⁿ⁾)´ = = .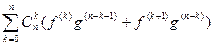

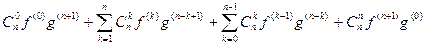Но 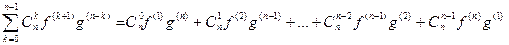= 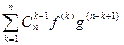и, принимая также во внимание свойства биномиальных коэффициентов: 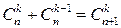, получаем

(fg)⁽ⁿ⁺¹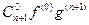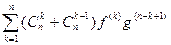⁾ = + + = , так что формула (1) верна, если заменить n на n+ 1 и теорема доказана.

Рассмотрим уравнение 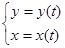(2)

Где , 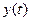− дважды дифференцируемые функции на некотором промежутке 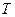; пусть, кроме того, функция строго возрастает (или убывает) на 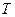и ни в одной точке этого промежутка 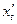не равна 0. В пункте 20.7 доказано, что в этом случае уравнения (2) задают функцию , и производная этой функции равна

Бывает также, что производные по параметру 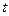обозначают так: 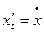, 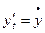. Тогда формула (3) принимает вид: 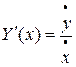. Найдём вторую производную функции :

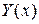5.Дифференциалы высших порядков.

Однородную линейную функцию называют линейной формой.

Напомним, что если функция 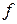дифференцируема в точке 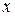, то

дифференциалом 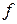в x называют линейную форму .

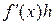Аналогично, если 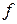дифференцируема дважды в точке ,

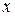то ее вторым дифференциалом называют квадратичную форму .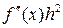

Вообще, n-ым дифференциалом 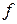в точке x будет n-ичная

форма 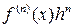(в предположении, что существует).

Для n-го дифференциала 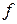в точке x используют обозначение 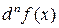или, более

строго .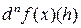

Таким образом, по определению,

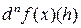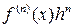= для всех 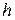Î . (2)

Согласно этому определению, 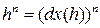есть n-я степень функци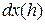и и

потому используют обозначение 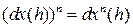. Тогда (2) примет вид

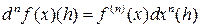для всех 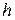Î , или равенства

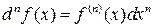. (3)

Форма (2) записи n-го дифференциала не инвариантна

уже при n=2. Действительно, подставляя вместо 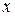дифференцируемую

функцию 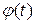в левую часть формулы (2) (при n=2), получим

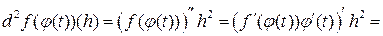
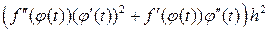= (4)

а в результате такой же подстановки в правую часть, имеем

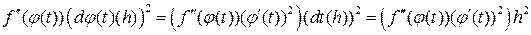.(5)

Правые части формул (5) и (4) отличаются слагаемым .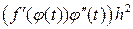

Вообще говоря, это слагаемое не равно нулю. Однако если 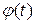- линейная функция,

то 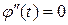и, вообще, для любого 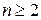имеет место равенство ,

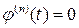откуда следует, что формула (3) будет верна и для линейной функции .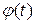

Дата добавления: 2015-04-24