
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Производная функции, заданной параметрически
|
|
|
|
.
Тогда сложная функция имеет производную, равную
► Придадим  приращение
приращение 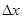 такое, что соответствующее значение
такое, что соответствующее значение  принадлежит окрестности точки
принадлежит окрестности точки 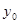 , в которой определена функция
, в которой определена функция 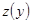 . Так как
. Так как 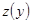 , по условию, дифференцируема в точке
, по условию, дифференцируема в точке 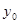 ,
,
 , где
, где  при
при  и
и 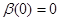 .
.
Так как  дифференцируема в точке
дифференцируема в точке  ,
,
 ,где
,где 
 . Как установлено в теореме 19.1, если
. Как установлено в теореме 19.1, если  , то и
, то и  .
.
Поэтому

Так как при  и
и  ,
,  ,
,  − бесконечно малые, из этого равенства следует, что
− бесконечно малые, из этого равенства следует, что
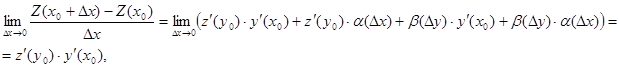 что и требовалось доказать.►
что и требовалось доказать.►
Рассмотрим уравнение 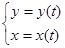 (1)
(1)
Где  ,
, 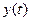 − дифференцируемые функции на некотором промежутке
− дифференцируемые функции на некотором промежутке 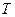 ; пусть, кроме того, функция
; пусть, кроме того, функция  строго возрастает (или убывает) на
строго возрастает (или убывает) на 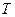 и ни в одной точке этого промежутка
и ни в одной точке этого промежутка 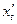 не равна 0.
не равна 0.
Символ 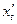 использован здесь для обозначения производной функции
использован здесь для обозначения производной функции 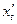 по переменной
по переменной 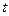 . Тогда, по теореме 17.4, существует обратная функция
. Тогда, по теореме 17.4, существует обратная функция  , причем ее производная, по теореме 20.1, равна
, причем ее производная, по теореме 20.1, равна
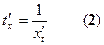
Но тогда уравнения задают  , и производная этой функции
, и производная этой функции  , по теореме 20.2 о производной сложной функции. Используя равенство (2), окончательно получаем:
, по теореме 20.2 о производной сложной функции. Используя равенство (2), окончательно получаем:

Часто вместо равенства (3) записывают равносильное ему равенство
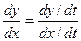
Бывает также, что производные по параметру 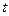 обозначают так:
обозначают так: 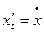 ,
, 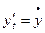 . Тогда формула (3) принимает вид:
. Тогда формула (3) принимает вид:  .
.
Вопрос 20: ДИФФЕРЕНЦИАЛ. ИНВАРИАНТНОСТЬ ФОРМЫ ПЕРВОГО ДИФФЕРЕНЦИАЛА
1. Понятие дифференциала числовой функции
Определение 1. Если числовая функция 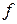 дифференцируема в точке
дифференцируема в точке 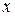 , то ее дифференциалом
, то ее дифференциалом 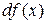 в этой точке называют однородную линейную функцию
в этой точке называют однородную линейную функцию 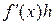 (новой) независимой переменной
(новой) независимой переменной 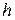 .
.
Таким образом,
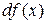 =
= 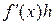 (1)
(1)
Положив в формуле (1)  , получим
, получим
 (2)
(2)
так что дифференциал 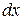 функции
функции  в каждой точке
в каждой точке 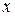 есть
есть
тождественная функция. Подставляя (2) в правую часть (1), получаем
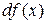 =
= 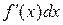 , (3)
, (3)
равенство двух линейных функций 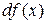 и
и 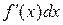 . Из него следует, что часто используемое обозначение производной
. Из него следует, что часто используемое обозначение производной  можно рассматривать, как отношение дифференциалов
можно рассматривать, как отношение дифференциалов 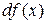 и
и 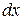 .
.
Функция 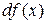 определена для всех действительных значений
определена для всех действительных значений 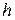 . Однако по традиции часто рассматривают
. Однако по традиции часто рассматривают 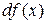 лишь на множестве тех
лишь на множестве тех 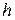 , для которых
, для которых  принадлежит области определения функции; т.е., лишь на множестве приращений аргумента
принадлежит области определения функции; т.е., лишь на множестве приращений аргумента 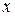 функции
функции 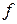 . Это объясняется тем, что дифференциал тесно связан с приращением функции. Так как, по предположению,
. Это объясняется тем, что дифференциал тесно связан с приращением функции. Так как, по предположению, 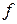 дифференцируема в точке x, то
дифференцируема в точке x, то
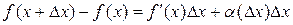 , (4)
, (4)
где 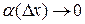 при
при  и первое слагаемое в правой части (4) – дифференциал, но рассматриваемый только для
и первое слагаемое в правой части (4) – дифференциал, но рассматриваемый только для  . Если
. Если 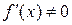 , то
, то  ,поэтому говорят, что «дифференциал есть главная линейная часть приращения функции».
,поэтому говорят, что «дифференциал есть главная линейная часть приращения функции».
2. Геометрический и механический смысл дифференциала.
Пусть числовая функция 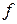 дифференцируема в точке
дифференцируема в точке 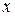 . Как известно, ее график имеет в точке
. Как известно, ее график имеет в точке 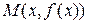 касательную с угловым коэффициентом
касательную с угловым коэффициентом  .
.

Теорема 20.1. Значение 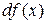 =
= 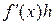 дифференциала равно приращению ординаты этой касательной при переходе от
дифференциала равно приращению ординаты этой касательной при переходе от 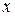 к
к  (см. рис.).
(см. рис.).
►Действительно, 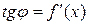 ,
,  ,поэтому
,поэтому  . Из рисунка также видно, что
. Из рисунка также видно, что  есть часть приращения
есть часть приращения 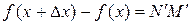 функции, стремящееся к совпадению с ним при
функции, стремящееся к совпадению с ним при  .◄
.◄
Дифференциал допускает и механическое толкование. Если 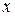 – время, а
– время, а  – путь, пройденный прямолинейно движущейся точкой к моменту
– путь, пройденный прямолинейно движущейся точкой к моменту 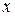 , то
, то  - ее скорость в данный момент. Тогда
- ее скорость в данный момент. Тогда 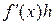 равен длине пути, который прошла бы точка за промежуток времени от
равен длине пути, который прошла бы точка за промежуток времени от 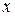 до
до  , если бы ее скорость оставалась неизменной (т.е. приложенные силы уравновесились).
, если бы ее скорость оставалась неизменной (т.е. приложенные силы уравновесились).
3. Инвариантность формы первого дифференциала
Правило дифференцирования сложной функции приведет нас к одному замечательному и важному свойству дифференциала.
Пусть функции  и
и 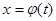 таковы, что из них может быть составлена сложная функция:
таковы, что из них может быть составлена сложная функция: 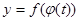 . Если существуют производные
. Если существуют производные  и
и 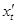 , то по теореме 20.2 существует и производная
, то по теореме 20.2 существует и производная
 (5)
(5)
Дифференциал 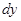 , если
, если  считать независимой переменной, выразится по формуле (3). Перейдём теперь к независимой переменной
считать независимой переменной, выразится по формуле (3). Перейдём теперь к независимой переменной  ; в этом предположении имеем другое выражение для дифференциала:
; в этом предположении имеем другое выражение для дифференциала:
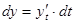 .
.
Заменяя производную 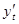 её выражением (5) и замечая, что
её выражением (5) и замечая, что  есть дифференциал
есть дифференциал  как функции от
как функции от  , окончательно получим:
, окончательно получим:
 ,
,
т. е. вернёмся к прежней форме дифференциала.
Таким образом, мы видим, что
|
|
|
|
|
Дата добавления: 2015-04-24; Просмотров: 449; Нарушение авторских прав?; Мы поможем в написании вашей работы!