Предельные величины

Лемма 19.1. Если функция дифференцируема в точке, и то функция дифференцируема в точке, причем

Теорема 19.9. Если функции и дифференцируемы в точке, и то их частное дифференцируемо в точке, причем

.

◄ Сначала докажем лемму

.

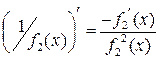◄ Приращение имеет вид:

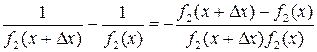
По лемме 8.2 функция определена в окрестности точки и по лемме 8.3. Следовательно,

. ►

Теорема 19.9 сразу следует из теоремы 19.8 и леммы 19.1.

Пусть обозначает величину издержек производства, рассматриваемую, как функцию от количества выпускаемой продукции. Если 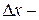прирост продукции, 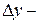приращение издержек производства, то 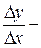среднее приращение издержек производства на единицу продукции. Производная 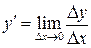выражает предельные издержки производства и является приблизительной характеристикой дополнительных затрат на производство единицы дополнительной продукции.

Вполне аналогично определяются предельная выручка, предельный доход, предельная полезность и т.п.

Предельные величины также часто называют маржинальными.

Дата добавления: 2015-04-24