
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Таким образом, нахождение углового коэффициента касательной (как и нахождение скорости) приводит к вычислению производной
|
|
|
|
Теорема 19.4. Если функция, определенная на промежутке, дифференцируема в его точке, то график этой функции имеет в соответствующей точке касательную, причем угловой коэффициент касательной равен.
Как и нахождение скорости неравномерного движения, нахождение касательной к кривой линии - одна из основных задач, решение которых привело к созданию дифференциального исчисления.
Таким образом, сказать, что числовая функция дифференцируема в данной точке, или что она имеет в этой точке производную, одно и то же. Нахождение производной функции у функции называют дифференцированием этой функции.
3. Касательная к графику функции
Рассмотрим частный случай задачи о касательной, когда линией служит график функции.
Определение 19.3. Пусть числовая функция  определена на невырожденном промежутке
определена на невырожденном промежутке  и непрерывна в его точке
и непрерывна в его точке 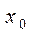 (так что расстояние
(так что расстояние  от соответствующей точки
от соответствующей точки  графика до его точки
графика до его точки  ,
,  , стремится к нулю при
, стремится к нулю при  ). Касательной к графику функции
). Касательной к графику функции  в точке
в точке  называют такую прямую, проходящую через
называют такую прямую, проходящую через  , что отношение расстояния
, что отношение расстояния 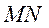 от точки
от точки  до этой прямой к расстоянию
до этой прямой к расстоянию  от
от  до
до  стремится к нулю при
стремится к нулю при  (т.е. что
(т.е. что 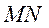 бесконечно мало по сравнению с
бесконечно мало по сравнению с  при
при  ).
).
Суть этого определения можно наглядно описать следующим образом: если представить, что точка  движется по линии к точке касания
движется по линии к точке касания  , то, какова бы ни была точность наблюдения, с некоторого момента точка
, то, какова бы ни была точность наблюдения, с некоторого момента точка  , будучи еще отличной от
, будучи еще отличной от  , уже неотличима от своей проекции
, уже неотличима от своей проекции  на касательную (рис. 14). Таким образом, кривая, обладающая в точке
на касательную (рис. 14). Таким образом, кривая, обладающая в точке  касательной, почти сливается с ней вблизи этой точки.
касательной, почти сливается с ней вблизи этой точки.
◄ По условию и по теореме 19.2 предыдущего пункта, представление

 , (5)
, (5)
 справедливо для всех
справедливо для всех  , принадлежащих некоторой окрестности
, принадлежащих некоторой окрестности  точки
точки  , и
, и  при
при  . Прямая с угловым коэффициентом
. Прямая с угловым коэффициентом  , проходящая через точку
, проходящая через точку  , имеет уравнение
, имеет уравнение
 . (6)
. (6)
Пусть  - точка графика с абсциссой
- точка графика с абсциссой  и
и  (рис. 15),
(рис. 15),  - проекция этой точки на прямую (6) и
- проекция этой точки на прямую (6) и  - точка этой прямой с абсциссой
- точка этой прямой с абсциссой  . Тогда направленный отрезок
. Тогда направленный отрезок 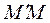 равен
равен  , так что, вычитая (8) из (7), получаем
, так что, вычитая (8) из (7), получаем  . Так как
. Так как  , а
, а 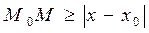 , то
, то  . Но
. Но 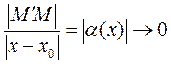 при
при  . Следовательно,
. Следовательно,  при
при  , т.е. (7) - уравнение касательной к графику функции
, т.е. (7) - уравнение касательной к графику функции  в его точке
в его точке  . ►
. ►
Замечание 1. Секущая 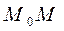 имеет угловой коэффициент
имеет угловой коэффициент  (см. рис. 15). Таким образом теорема 1 показывает, что угловой коэффициент касательной в точке
(см. рис. 15). Таким образом теорема 1 показывает, что угловой коэффициент касательной в точке  есть предел углового коэффициента секущей
есть предел углового коэффициента секущей 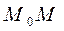 при
при  .
.
|
|
|
|
|
Дата добавления: 2015-04-24; Просмотров: 436; Нарушение авторских прав?; Мы поможем в написании вашей работы!