Решение. Каждой формуле алгебры высказываний соответствует один многочлен Жегалкина

Каждой формуле алгебры высказываний соответствует один многочлен Жегалкина. Равносильным формулам соответствует один и тот же многочлен Жегалкина. Обратно, каждому многочлену Жегалкина соответствует формула алгебры высказываний. Однако обратное соответствие не является однозначным. Одному многочлену Жегалкина может соответствовать несколько равносильных формул.

Упростим данную формулу (естественно, если упрощение возвожно). Запишем данную формулу:

;

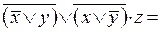дважды применим формулу 15 (первый закон де Моргана):

;

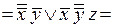дважды применим формулу 21 (закон снятия двойного отрицания):

;

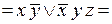применим формулу 21 (расставим двойное отрицание):

;

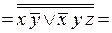последовательно избавимся от операции отрицания; к верхнему отрицанию применим формулу :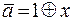

;

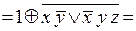применим формулу 15:

;

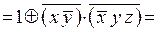дважды применим формулу :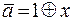

;

дважды применим формулу :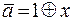

;

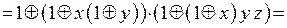дважды применим формулу :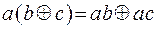

.

перемножим скобки, применяя формулу :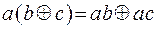

.

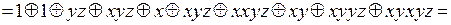упростим сумму, применяя формулы , и :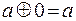

.

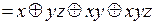Ответ: – многочлен Жегалкина.

Задание № 8. Упростить данную релейно-контактную схему.

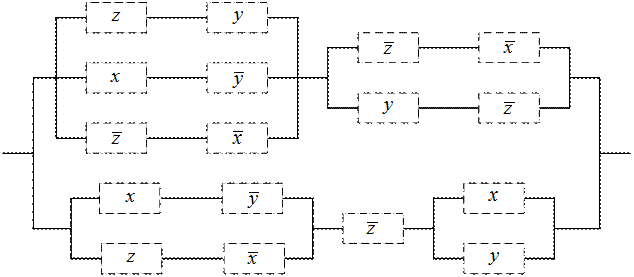
Дата добавления: 2015-04-24