Задачи, приводящие к понятию производной

Методическая разработка

для студентов лечебного, педиатрического, стоматологического

и медико-профилактического факультетов

к лабораторной работе

«Основные понятия математического анализа»

1. Научно-методическое обоснование темы:

Понятия производной и дифференциала являются одними из основных понятий математического анализа. Вычисление производных необходимо при решении многих задач в физике и математике (нахождение скорости, ускорения, давления и т. д.). Важность понятия производной, в частности, определяется тем, что производная функции характеризует скорость изменения этой функции при изменении ее аргумента.

Применение дифференциала позволяет осуществить приближенные вычисления, а также проводить оценку погрешностей.

Способы нахождения производных и дифференциалов функций и их применение составляют основную задачу дифференциального исчисления. Необходимость понятия производной возникает в связи с постановкой задачи о вычислении скорости движения и нахождении угла касательной к кривой. Возможна и обратная задача: по скорости определить пройденный путь, а по тангенсу угла наклона касательной найти соответствующую функцию. Такая обратная задача приводит к понятию неопределенного интеграла.

Понятие определенного интеграла используют в ряде практических задач, в частности в задачах по вычислению площадей плоских фигур, расчету работы, производимой переменной силой, нахождению среднего значения функции.

При математическом описании различных физических, химических, биологических процессов и явлений часто используют уравнения, содержащие не только изучаемые величины, но и их производные различных порядков от этих величин. Например, в соответствии с простейшей версией закона размножения бактерий, скорость размножения пропорциональна количеству бактерий в данный момент времени. Если это количество обозначить через N(t), то в соответствии с физическим смыслом производной скорость размножения бактерий представляет собой производную N(t), и на основании упомянутого закона можно записать соотношение N'(t)=к∙N, где к>0 - коэффициент пропорциональности. Полученное уравнение не является алгебраическим, так как содержит не только неизвестную функцию N(t), но и ее производную первого порядка.

2. Краткая теория:

1. Задача о нахождении скорости v материальной точки. Пусть некоторая материальная точка совершает прямолинейное движение. В момент времени t₁ точка находится в положении М_1. В момент времени t₂ в положении М₂. Обозначим промежуток М₁, М₂ через ΔS; t₂ – t₁ =Δt. Величина 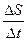называется средней скоростью движения. Чтобы найти мгновенную скорость точки в положении М₁ необходимо Δt устремить к нулю. Математически это значит, что

, (1)

Таким образом, для нахождения мгновенной скорости материальной точки необходимо вычислить предел отношения приращения функции ΔS к приращению аргумента Δt при условии, что Δt→0.

2. Задача о нахождении угла наклона касательной к графику функции.

Рис.1

Рассмотрим график некоторой функции у=f(х). Чему равен угол наклона 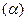касательной, проведенной в точке М₁? В точке М₁ проведем касательную к графику функции. На графике выберем произвольную точку М₂ и проведем секущую. Она наклонена к оси ОХ под углом α₁. Рассмотрим ΔМ₁М₂А:

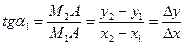, (2)

Если точку М₁ фиксировать, а точку М₂ приближать к М₁, то секущая М₁М₂ будет переходить в касательную к графику функции в точке М₁ и можно записать:

, (3)

Таким образом, необходимо вычислить предел отношения приращения функции к приращению аргумента, если приращение аргумента стремится к нулю.

Предел отношения приращения Δy функции у=f(х) к приращению аргумента Δx в заданной точке х₀ при стремлении Δx к нулю, называется производной функции в заданной точке.

Обозначения производной: у', f '(х), 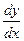. По определению

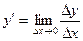, (4)

где Δx=х₂-х₁ – приращение аргумента (разность между двумя последующими достаточно близкими значениями аргумента), Δy=у₂-у₁ – приращение функции (разность между значениями функции, соответствующими этим значениям аргумента).

Нахождение производной данной функции называется ее дифференцированием. Дифференцирование основных элементарных функций производится по готовым формулам (см. табл.), а также с помощью правил:

1. Производная алгебраической суммы функций равна сумме производных этих функций:

(u+υ)'= u' +υ'

2. Производная произведения двух функций равна сумме произведений второй функции на производную первой и первой функции на производную второй:

(u∙ υ)'= u' υ + u υ'

3. Производная частного двух функций равна дроби, числитель которой есть разность между произведениями знаменателя на производную числителя и числителя на производную знаменателя, а знаменатель- квадрат знаменателя:

Физический смысл производной. Из сравнения (4) и (1) следует, что мгновенная скорость прямолинейного движения материальной точки равна производной зависимости ее координаты от времени.

Общий смысл производной функции заключается в том, что она характеризует скорость (быстроту) изменения функции при данном изменении аргумента. Быстрота протекания физических, химических и других процессов, например скорость охлаждения тела, скорость химической реакции, скорость размножения бактерий и т.п., также выражается при помощи производной.

Геометрический смысл производной. Величину тангенса угла наклона касательной, проведенной к графику функции, в математике называют угловым коэффициентом касательной.

Угловой коэффициент касательной, проведенной к графику дифференцируемой функции в некоторой точке, численно равен производной функции в данной точке.

Это утверждение называют геометрическим смыслом производной.

Дата добавления: 2015-04-24