Дифференциал функции

Из уравнения (4) можно записать равенство

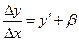, (6)

где 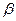- некоторая величина. При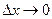 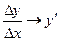, т.е. 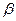тоже стремится к нулю. Преобразовав (6) имеем:

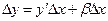, (7)

Из (7) видно, что приращение функции состоит из двух слагаемых. Слагаемое 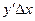называют главной частью приращения функции 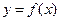или дифференциалом функции.

Дифференциал функции равен произведению производной функции на приращение аргумента и символически обозначается :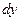

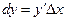, (8)

-

Рис.2

Таким образом, дифференциал функции, в общем случае отличаясь от приращения функции, представляет собой главную часть этого приращения, линейную относительно приращения аргумента. В этом заключается аналитический смысл дифференциала.

Отсюда следует, что при достаточно малых приращениях аргумента величина приращения функции приближенно равна дифференциалу этой функции:

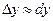, (9)

Для выяснения геометрического смысла дифференциала рассмотрим график функции 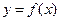, изображенный на рис.2. В точке М проведем касательную. Рассмотрим 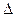АВМ. Катет МВ равен приращению аргумента 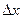; ; 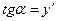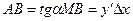.Итак, .

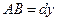Таким образом, дифференциал функции является приращением ординаты касательной (АВ), которое соответствует приращению 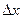(МВ) абсциссы. В этом заключается геометрический смысл дифференциала.

Дифференциалом аргумента называют приращение аргумента, т.е.

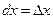, (10)

С учетом (10) можно записать:

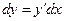, (11)

Дата добавления: 2015-04-24