З а д а ч а 24

Пример 25

З а д а ч а 23

Пример 24

З а д а ч а 22

Пример 23

Вычислить . Это неопределенность вида .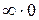

Так как .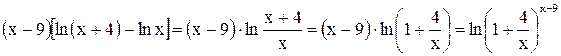

Найдем, используя свойство непрерывности логарифмической функции:

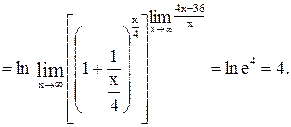
Контрольные варианты к задаче 21

Вычислить пределы функции:

1. 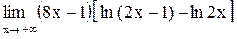.	2. .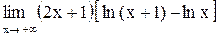
3. 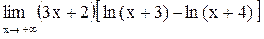.	4. .
5. 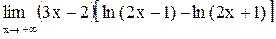.	6. .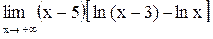
7. 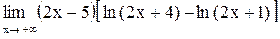.	8. .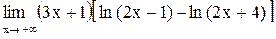
9. 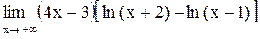.	10. .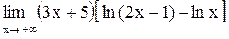
11. 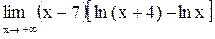.	12. .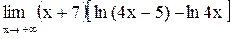
13. .	14. .
15. 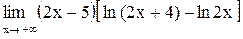.	16. .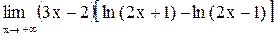
17. 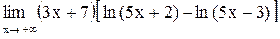.	18. .
19. 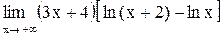.	20. .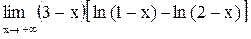
21. 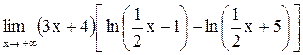.	22. .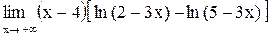
23. .	24. .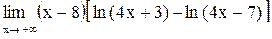
25. 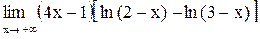.	26. .
27. 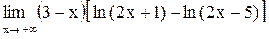.	28. .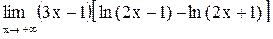
29. 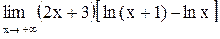.	30. .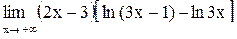

Вычислить .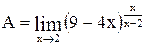

Если представить предельное значение переменной х, то получим неопределенность вида 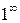. Используя вторую форму второго замечательного предела

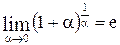, введем новую переменную 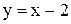. Тогда , если . Из замены 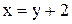. Тогда

Контрольные варианты к задаче 22

Вычислить пределы функций

.	.	.
.	.	.
.	.	.
.	.	.
.	.	.
.	.	.
.	.	.
.	.	.
.	.	.
.	.	.

.

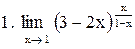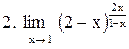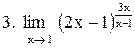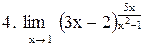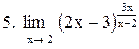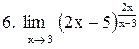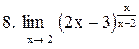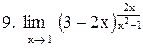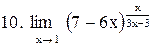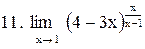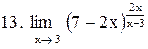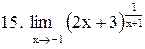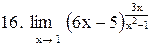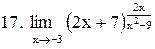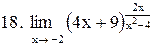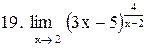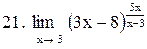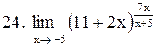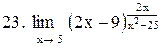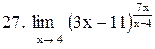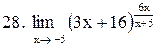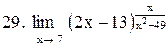При подстановке предельного значения аргумента возникает неопределенность 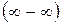. Приведение к общему знаменателю сводит эту неопределенность к

неопределенност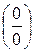и или .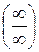

.

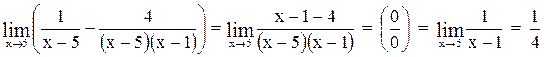Контрольные варианты задачи 23

Вычислить пределы функций:

.	.
.	.
.	.
.	.
.	.
.	.
.	.
.	.
.	.
.	.
.	.
.	.
.	.
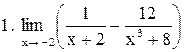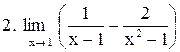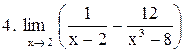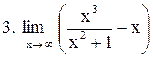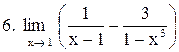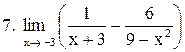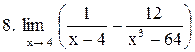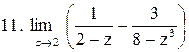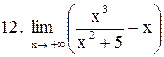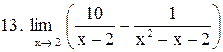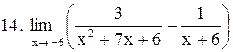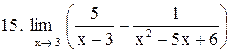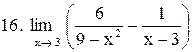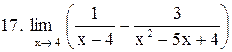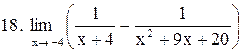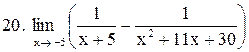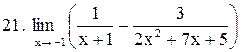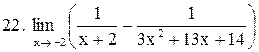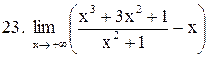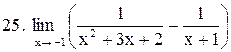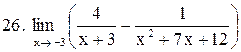27..	.
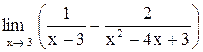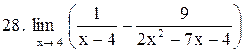29..	.

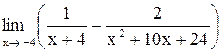Функция 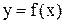непрерывна в точке 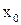, если выполнены условия:

1) функция определена в этой точке и ее окрестности;

2) существует предел функции в точке 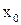, т. е. ;

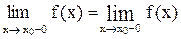3) предел функции в точке 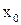равен значению функции в этой точке.

Если в точке 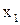нарушено хотя бы одно из этих условий, то 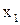- точка разрыва.

Точка разрыва 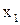называется точкой разрыва первого рода, если существуют конечные односторонние пределы функции в этой точке. Если при этом они равны между собой, то 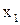называют точкой устранимого разрыва, а если они не равны, то 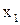называют точкой неустранимого разрыва или скачком.

Точка разрыва 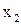называется точкой разрыва второго рода, если хотя бы один (или оба) из односторонних пределов функции в точке 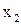бесконечен или

не существует.

Дата добавления: 2015-04-24