М. Н. Полякова, А. М. Вербенец 5 страница

1) каждое из множеств К\, К₂,... К„ непустое, т. е. Kj*0, где / = 1, 2, 3,.., я;

2) эти множества попарно не пересекаются, т. е. Kji~\Kj = 0 для всяких fcj и 1, 2, 3,.., п;

3) их объединение образует множество М, т. е. К_{иК₂и...К„ = М.

Если хотя бы одно из условий (1)—(3) не выполняется, то сис­тема множества К\, К₂,.., К„ не является разбиением множества М на классы. Например, система множества остроугольных, прямо­угольных и двупрямоугольных треугольников не образует разбие­ние множества всех треугольников, так как множество двупрямо­угольных треугольников, содержащих по два прямых угла, пусто, т.е. не выполняется условие (1). Система множеств остроуголь­ных, прямоугольных и равнобедренных треугольников не образу­ет разбиение множества всех треугольников, так как не выполня­ется условие (2) — множества прямоугольных и равнобедренных треугольников пересекаются (существуют прямоугольные равно­бедренные треугольники). Система множества остроугольных и прямоугольных треугольников не образует разбиения множества треугольников, так как не выполняется условие (3) — объедине­ние множеств остроугольных и прямоугольных треугольников не образует множество всех треугольников.

Отношения между двумя множествами

С целью уточнения вернемся к вопросу об отношении вклю­чения одного множества в другое.

Вообще говоря, в математике различаются два вида включе­ния: в широком смысле (нестрогое включение) и в узком смысле (строгое включение). Первое обозначается знаком с. Запись «AczB» означает, что все элементы Л принадлежат В. При этом воз­можны два случая:

1) все элементы В принадлежат А, т. е. AczB и ВсА. В этом слу­чае множества An В состоят из одних и тех же элементов и назы­ваются равными, что обозначается так: «А=В». Например, если А — множество всех больших блоков, а В — множество всех бло­ков, которые не являются малыми, то А=В. Как видно, равные множества по существу совпадают (при задании их перечислени­ем элементов они могут отличаться лишь порядком перечисления, который несуществен);

2) не все элементы В принадлежат А, т. е. AciB, но BczA. В таком случае говорят также, что А строго включается в В — или А является собственной (или правильной) частью В. Это отношение в матема­тической литературе обычно обозначается символом «с» {A(zB).

В предматематической подготовке дошкольников встречается лишь строгое включение, собственная часть множества.

В играх с обручами моделируются и другие отношения, в кото­рых могут находиться два множества. Так, например, множества красных (А) и не красных (Л) блоков не имеют ни одного общего элемента, т. е. их пересечение пусто (АглА = 0). Такие два множест­ва, как мы уже знаем, называются непересекающимися (в литературе встречается и термин «дизъюнктные» множества). Множества красных (А) и квадратных (В) блоков имеют общие элементы (крас­ные квадраты), т. е. их пересечение непусто (АглВф0), причем ни одно из этих множеств не включается в другое, т. е. не является подмножеством другого. Такие два множества называются пересе­кающимися.

Выявление правильных отношений между множествами окру­жающих нас предметов — составная часть формирования и разви­тия представлений дошкольников об окружающем мире. Выработ­ка у дошкольников простейших представлений классификации ок­ружающих предметов является основой для формирования в дальнейшем математического мышления, связанного с моделиро­ванием и исследованием различных математических конструкций, способствует повышению алгоритмической культуры учащихся.

2.2. Отношения

Бинарные отношения

Под бинарным отношением понимают отношение между двумя предметами. Дальше, говоря «отношение», мы будем иметь в виду именно бинарное отношение. Выясним, что интуитивно понима­ют под отношением и как это понятие можно описать математи­чески.

Из курса школьной математики известны многочисленные примеры отношений:

• между числами: равно, не равно, меньше, больше, не меньше, не больше, делит, делится на;

• между точками прямой: предшествует, следует за;

• между прямыми: параллельны, пересекаются, перпендикулярны, скрещиваются;

• между прямой и плоскостью: параллельны, пересекаются, пер­пендикулярны;

• между плоскостями: параллельны, пересекаются, перпендику­лярны;

• между геометрическими фигурами: равно, подобно и др.

Это, разумеется, далеко не полный перечень встречающихся в школьной математике отношений.

Примеры бинарных отношений встречаются не только в ма­тематике, но и всюду в жизни, вокруг нас. Родственные и другие отношения между людьми (быть отцом, дедушкой, матерью, ба­бушкой, братом, сестрой, другом, ровесником; старше, моложе, выше, ниже и др.) выступают как бинарные отношения. Отноше­ния между событиями во времени (раньше, позже, одновременно), между предметами по их расположению в пространстве (выше, ниже, левее, правее, севернее, южнее и др.) также выступают как бинарные отношения.

Всегда, когда речь идет о некотором отношении, имеются в виду два множества А я В; при этом некоторые элементы множе­ства А находятся в данном отношении с некоторыми элементами множества В или того же множества А.

Таким образом, всякое отношение между элементами мно­жеств А и В (или между элементами множества А) порождает мно­жество пар, первые компоненты которых принадлежат А, вто­рые — В (или тоже А), т. е. порождает подмножество АхВ (или АхА), причем такое, что элементы каждой пары и только они на­ходятся в данном отношении.

Всякое отношение между элементами двух множеств А и В полностью характеризуется тремя множествами: А и В, между эле­ментами которых установлено отношение, и некоторым множест­вом пар Р — подмножеством АхВ, т. е. декартовым произведением. Один из путей определения математического понятия отношения и состоит в отождествлении этого понятия с указанной тройкой множеств.

Отношением между элементами непустых множеств А и В на­зывается тройка множеств р=(Р, А, В), где P<zAxB.

Множество пар Р называется графиком отношения р.

Об элементах пары (х, у), принадлежащей графику Р, говорят, что они находятся в отношении р, и записывают это так: «хру».

Таким образом, записи «(х, у)е Р» или «хру» равносильны.

Если В—А, то р=(Р, А, А) называется отношением между эле­ментами множества А.

Свойства отношений

1. Отношение р на множестве А является рефлексивным, если всякий элемент этого множества находится в отношении р с самим собой. Если же каждый элемент множества А не находится в этом отношении с самим собой, отношение обладает свойством антирефлексивности и называется антирефлексивным.

Среди уже перечисленных нами отношений рефлексивными являются: равно, не меньше, не больше, делит, делится на, равенство и подобие фигур; антирефлексивными являются отношения: нерав­но, меньше, больше между числами; предшествует, следует за между точками прямой. Отношение быть ровесником между людь­ми является рефлексивным, отношение же быть отцом, быть ма­терью, выше, старше, моложе — антирефлексивными. Отношение быть другом не является ни рефлексивным, ни антирефлексив­ным (бывают случаи, когда человек сам себе друг, и случаи, когда человек сам себе недруг).

2. Рассмотрим свойство: если а-b, то Ь=а, т. е. если пара (а, Ь)
находится в отношении равно, то и пара (Ь, а) находится в этом
отношении.

Таким свойством обладает, например, отношение быть ровес­ником: если х ровеснику, то у ровесник х. Это отношение обладает свойством симметричности и называется симметричным.

Не является симметричным, например, отношение старше: если х старше у, то неверно, что у старше х. Подобные отношения обладают свойством асимметричности и называются асиммет­ричными.

3. Несложно установить истинность следующих утверждений:
если х<у и y<z, то x<z;

если х=у и ущ, то x=z;

если х ровесник у и у ровесник z, то х ровесник z; если х старше у и у старше z, то х старше z; если а\\Ь и Ь\\с, то а\\с.

Однако если х — отец у и у — отец z, то z не есть отец z (он его дедушка); если х — друг у, а у — друг z, то вообще не известно, является ли х другом z.

Свойство отношения р—(Р, А, А), состоящее в том, что из хру и ypz следует xpz для любых х, y,z^A, называется транзитивностью, а отношение р, обладающее этим свойством, — транзитивным.

Свойство отношения р, состоящее в том, что из хру и ypz сле­дует —xpz для любых х, у, zЈ А, называется антитранзитивностью, а отношение р, обладающее этим свойством, — антитранзитив­ным.

Так, отношения меньше, равно, быть ровесником, старше, па­раллельно являются транзитивными. Отношение быть отцом яв­ляется антитранзитивным, а отношение быть другом не является ни транзитивным, ни антитранзитивным.

Отношение эквивалентности

Выделим теперь класс отношений, играющих особую роль в разбиении множеств предметов на классы, т. е. в классификации множеств.

Среди рассмотренных выше примеров отношений имеются такие, которые являются рефлексивными, симметричными и транзитивными одновременно. К ним относятся отношения ра­венства чисел и геометрических фигур, подобия фигур, отноше­ние быть ровесником.

Эти и другие подобные им, т. е. обладающие такими же свойст­вами, отношения принадлежат важному классу отношений эквива­лентности, находящих широкое применение и использование, в том числе в курсе математики общеобразовательной школы.

Всякое рефлексивное, симметричное и транзитивное отноше­ние, установленное в некотором множестве А, называется отно­шением эквивалентности.

Если между элементами некоторого множества введено или ус­тановлено отношение эквивалентности, то этим самым порождает­ся разбиение данного множества на классы таким образом, что любые два элемента, принадлежащие одному классу разбиения, на­ходятся в данном отношении (иначе: эквивалентны по этому отно­шению), любые же два элемента, принадлежащие различным клас­сам, не находятся в этом отношении (иначе: не эквивалентны по этому отношению). Такое разбиение множества на классы обычно называют разбиением множества на классы эквивалентности.

Разбиение множества блоков (или фигур) на классы эквива­лентности можно смоделировать с помощью следующей игры с тремя обручами.

В множестве всех блоков введем отношение иметь один цвет (или быть одного цвета). Нетрудно убедиться в том, что это

множества всех блоков на классы эквивалентности по отношению быть одного цвета (области (1), (2), (3), (4) оказываются пустыми, так как нет трехцветного или двухцветного блока, область (8) пуста, так как блоков другого цвета, кроме красного, синего или желтого, нет). Нетрудно убедиться в том, что удовлетворяются условия (1)—(3) правильного разбиения (см. 2.1): 1) ни один из классов (красных, синих, желтых) блоков не пуст; 2) эти классы попарно не пересекаются; 3) их объединение равно множеству Мвсех блоков.

Таким же путем, т. е. с помощью отношения быть одного цвета, формируется и само представление о цвете как о классе, объединяющем все предметы одного цвета, скажем все красные предметы.

Аналогично формируется и представление об определенной форме предметов. С помощью отношения иметь одну форму мы

получаем разбиение всех блоков (или фигур) на четыре класса эк­вивалентности такое, что любые два блока (или две фигуры), при­надлежащие одному классу, обладают одной и той же формой, любые же два блока (или две фигуры) различных классов облада­ют различной формой. Сама форма выступает здесь как класс эк­вивалентности. Так, впоследствии, например, формируются представления о круге, квадрате, треугольнике, прямоугольнике и других геометрических фигурах как на плоскости, так и в про­странстве.

Эти примеры показывают, с одной стороны, что отношения эквивалентности являются базой для формирования новых поня­тий и для классифицирующей деятельности, с другой — что рас­смотренные выше (2.1) дидактические игры с обручами обучают этой деятельности.

Отношение порядка

Среди рассмотренных выше примеров отношений имеются такие, как меньше, больше между числами, предшествует, следует за между точками прямой; старше, моложе между людьми. Эти от­ношения являются антирефлексивными, асимметричными и тран­зитивными.

Всякое антирефлексивное, антисимметричное и транзитивное отношение в некотором множестве А называется отношением по­рядка¹.

2.3. Числа

Возникновение понятия натурального числа

1 Иногда такое отношение называют отношением строгого порядка, чтобы отличить его <уг отношения нестрогого порядка, являющегося рефлексивным, антисимметричным и тран­зитивным.

Теоретические основы формирования элементарных матема­тических представлений у дошкольников включают детальное изу­чение лишь системы натуральных чисел. Поэтому, говоря здесь «числа», мы имеем в виду натуральные числа.

К построению математических моделей явлений, основанно­му на отвлечении от всех свойств предметов, кроме их количест­венных отношений и пространственных форм, человечество при­бегало с первых шагов изучения окружающего мира. Одним из первых достижений на этом пути было возникновение и форми­рование понятия натурального числа. Оно появилось, по-видимо­му, на довольно позднем этапе развития мышления и предполага­ло наличие способности к созданию абстрактных понятий и опе­рированию ими.

Процесс формирования понятия числа был сложным и дли­тельным. На самом раннем этапе устанавливалась равночислен-ность различных множеств, общее же свойство равночисленных множеств еще не отделялось от конкретной природы сравнивае­мых множеств. Например, знали, что два рыболова поймали по­ровну рыб, но не выражали этого каким-либо числом. В дальней­шем практика экономических и социальных взаимоотношений привела к необходимости выражать численность одних множеств уже через численность других множеств, т. е. общее свойство рав­ночисленное™ стало осознаваться как нечто отличное от кон­кретной природы самого множества, его элементов. Однако в ка­честве эталонов выступали еще различные множества, состоящие из подручных предметов — эквивалентов равночисленности мно­жеств предметов. Еще позже определенное множество, например пальцы на руках и ногах, начали выступать в качестве своеобраз­ного единственного эталона количества, что позволило выделить общее свойство численности, отличное от всех особенных свойств множеств. Впоследствии общее свойство всех равночисленных множеств абстрагировалось от самих множеств и выступило в «чистом виде», т. е. как абстрактное понятие натурального числа. Далее в качестве эталона численности уже выступают сами нату­ральные числа, когда люди говорят не «рука яблок», а «пять яблок» (интересно, что в слове «пять» сохранилось воспоминание о «пясти», т. е. о ладони). И наконец, происходит отвлечение от ре­ально существующих ограничений счета и возникает понятие о сколь угодно больших числах. Возникает абстракция бесконечного множества натуральных чисел. Объектом научного анализа стано­вятся свойства элементов самого этого множества, в отвлечении от тех предметов, счет которых привел к созданию понятия числа. Возникает теория, описывающая систему чисел с ее свойствами и закономерностями.

Как будет показано дальше, процесс формирования представ­лений дошкольников о числе в известном смысле в общих чертах повторяет основные этапы исторического развития этого понятия.

В математике известны различные способы построения тео­рии натуральных чисел. Мы рассмотрим лишь основные идеи двух теорий натуральных чисел, количественной и порядковой, находя­щие отражение в формировании представлений о числе, счете и арифметических операциях.

Основные идеи количественной теории натуральных чисел

В количественной теории натуральное число с самого начала воспринимается как число элементов (мощность, численность) конечного множества.

Рассмотрим всевозможные конечные множества (говорят «класс, или семейство, множеств») и установим для них отноше­ние эквивалентности следующим образом: два множества А и В будем называть эквивалентными (обозначается это через А~В), если между элементами этих множеств можно установить взаимно однозначное соответствие.

Установленное таким образом отношение множеств является отношением типа эквивалентности, т. е. оно рефлексивно, сим­метрично и транзитивно. Для любых множеств А, В, С:

а) А~А; б) если А~В, то В~А; в) если А~В и В~С, то А~С.

Поэтому введенное отношение порождает разбиение данного семейства множеств на классы эквивалентности так, что любые два множества одного класса эквивалентны, а любые два множе­ства различных классов неэквивалентны.

Эквивалентные множества не совпадают полностью, всеми своими свойствами: множество пальцев человеческой руки и мно­жество, состоящее из пяти столов, различные, но эквивалентные множества.

Каждый класс эквивалентности характеризуется мощностью, т. е. любые два множества одного класса равномощны (имеют одинаковую мощность). Так как мы имеем дело лишь с конечны­ми множествами, то равномощность означает равночисленность. Мощность, или класс, равночисленных конечных множеств и на­зывают натуральным числом.

Таким образом, каждому конечному множеству Л приписыва­ют в качестве характеристики натуральное число т(А), опреде­ляющее его принадлежность определенному классу эквивалент­ности. При этом множествам, принадлежащим одному классу эк­вивалентности, приписывается одно и то же натуральное число:

если А~В, то т(А)=т(В);

множествам, принадлежащим различным классам эквивалент­ности,— различные натуральные числа:

если А~В, то т (А)^т(В).

Так как А и В — конечные множества, то натуральные числа т(А) и т(В) обозначают числа элементов (численность) этих мно­жеств.

В основе такой концепции натурального числа лежит абстрак­ция отождествления: отношение эквивалентности множеств отож­дествляет множества, принадлежащие одному классу эквивалент­ности по их численности.

В результате этого отождествления от множеств, принадлежа­щих одному классу эквивалентности, абстрагируется их общее свойство, характеризующее этот класс, в виде самостоятельного понятия — натурального числа.

Название «количественная теория» связано с тем, что в этой теории натуральное число обозначает количество элементов мно­жества.

Основные идеи порядковой теории натуральных чисел

В конце XIX в. была построена порядковая теория натураль­ных чисел, которая обычно связывается с именем итальянского математика Джузеппе Пеано (1858—1932), построившего эту тео­рию на аксиоматической основе.

Весьма развитый в математике аксиоматический подход к по­строению теорий состоит в следующем: а) выделяются некоторые исходные, неопределяемые через другие понятия; все остальные понятия теории определяются через ранее уже определенные; б) выделяются некоторые исходные предложения, или аксиомы, истинность которых принимается без доказательства; все осталь­ные предложения теории — теоремы — логически выводятся или доказываются с использованием введенных понятий, ранее дока­занных фактов, теорем.

Отметим, что аксиоматический подход применяется для по­строения теории, о которой уже имеются определенные, сформи­рованные интуитивные представления. Иначе говоря, осуществ­ляется аксиоматизация уже имеющейся «предматематической теории».

Подход к построению теории натуральных чисел, берущий на­чало от Пеано, представляет собой определенный способ матема­тизации интуитивного представления о натуральном ряде.

Математизация этого интуитивного понятия приводит к опре­делению натурального ряда как некоторой структуры (T, 1,'), со­стоящей из: а) множества N, элементы которого называются нату­ральными числами; б) выделенного в этом множестве элемента, обозначаемого знаком 1 и называемого единицей; в) определенного в множестве ТУотношения «непосредственно следует за» (число, не­посредственно следующее за числом*, обозначим черезх\ т. е. если у непосредственно следует за х, то у=х'; у! — «сосед справа» для х).

Натуральный ряд обладает следующими интуитивно ясными свойствами (принятыми Пеано в качестве аксиом, характеризу­ющих эту структуру).

I. Единица непосредственно не следует ни за каким натураль­ным числом, т. е. не является «правым соседом» никакого другого натурального числа, это «первое» натуральное число.

П. Для любого натурального числа существует одно и только одно непосредственно следующее за ним натуральное число, т. е. любое натуральное число имеет только одного «правого соседа».

III. Любое натуральное число непосредственно следует не бо­лее чем за одним натуральным числом, т. е. единица не следует ни за каким, всякое другое натуральное число — точно за одним.

Всякое натуральное число, кроме единицы, является «правым соседом» одного и только одного натурального числа, его «левого соседа».

I. Если какое-нибудь множество М натуральных чисел (Л/c/) содержит 1 и вместе с некоторым натуральным числом х содержит и натуральное число х¹', непосредственно следующее за х, то это множество совпадает с множеством всех натуральных чисел (M=N).

Предложение I, хотя по своему содержанию более слож­но, чем первые три, также выражает достаточно простое свой­ство: с помощью последовательного прибавления единицы, на­чиная с единицы, можно получить все натуральные числа. Вся­кий раз, когда мы доходим до некоторого числа х, допускается возможность написания непосредственно следующего за ним числа х?.

Натуральный ряд в описанном представлении мыслится потенциально бесконечным. С этой точки зрения процесс его обра­зования незавершаем, предполагается лишь, что после каждого шага процесса мы располагаем возможностью осуществления сле­дующего шага.

Свойства I—I характеризуют структуру «натуральный ряд» только с точки зрения отношения ', названного «непосредствен­но следует за». Но это построение можно дополнить свойствами, характеризующими операции сложения и умножения в множе­стве N.

Расширим систему свойств I—I таким образом, чтобы полу­чить характеристику структуры (N, 1,', +, •).

Знак + обозначает операцию «сложение», сопоставляю­щую с каждой парой (х, у) натуральных чисел натуральное число х+у, называемое их суммой и обладающее следующими свойст­вами:

т. е. сумма любого натурального числа х с числом 1 равна непо­средственно следующему за х числу хЛ I. Х+у'=(х+у)',

т. е. сумма любого числа х с числом у', непосредственно следу­ющим за любым числом у, равна числу, непосредственно следу­ющему за суммой х+у.

Знак • обозначает операцию умножения, сопоставляющую с каждой парой (х, у) натуральных чисел натуральное число х»у, на­зываемое их произведением и обладающее следующими двумя свойствами: II.x»l=x,

т. е. произведение любого натурального числа х и числа 1 равно числу х (умножение какого-нибудь числа на единицу не меняет это число).

III. х»(У)=(х»у)+х, т. е. произведение числа х на число, непосредственно следующее за числом у, равно произведению чисел х и у, сложенному с чис­лом х.

Из свойств I—III выводятся все остальные свойства порядка и операций сложения и умножения натуральных чисел.

Покажем в качестве примера, как, исходя из перечисленных свойств, можно получить таблицу сложения.

Будем исходить из знания того, что непосредственно сле­дующее число за каждым однозначным числом уже получено:

Г=2; 2'=3; 3'=4; 4'=5; 5'=6; 6'=7; 7'=8; 8'=9; 9'=10.

Исходя из свойства, получаем таблицу «прибавления едини­цы»:

1 + 1=1'=2;

2+1=2'=3;

3+1=3'=4;

9+1=9'= 10.

Теперь, зная таблицу и используя свойство I, можем вывести, например, чему равно 2+2:

2+2=2+1'=(2+1)'=3'=4.

Аналогично 3+2=3+Г=(3+1)'=4'=5 и т. д.

Как видно, в описанном построении теории натуральных чисел основную роль играет операция (функция) прибавления единицы

/(х)=х+1,

сопоставляющая с каждым числом х непосредственно следующее за ним число х+1 (илихО- Эта идея используется в обучении счету маленьких детей.

2.4. Геометрические фигуры

Формирование понятия геометрической фигуры

Исторически понятие геометрической фигуры, так же как понятие натурального числа, было одним из исходных по­нятий математики. Как и натуральные числа, понятие геомет­рической фигуры образовалось с помощью абстракции отожде­ствления, в основе которой лежит некоторое отношение экви­валентности. В данном случае таким отношением является сходство, подобие предметов по их форме, с помощью которого множество предметов разбивается на классы эквивалентности так, что любые два предмета одного класса имеют одинаковую форму, а любые два предмета различных классов — различные формы. Абстрагируясь при этом от других свойств предметов (цвета, величины, материала, из которого они сделаны, назна­чения и т. д.), мы получаем самостоятельное понятие геометри­ческой фигуры.

В математике поступают и так: класс подобных по форме предметов определяется любым принадлежащим ему предметом и называется формой.

В связи с рассмотрением отношения эквивалентности нами был приведен пример классификации блоков по их форме. Решая эту задачу, дети получают классы квадратных, круглых, треугольных и прямоугольных блоков, затем каждый из этих классов, так же как и отдельные их представители, называется соответственно квадратом, кругом, треугольником, прямоуголь­ником. В основе выделения этих понятий лежит отношение эк­вивалентности иметь одинаковую форму.

В изучении геометрии, и в частности геометрических фигур, различают несколько уровней мышления.

Первый, самый простейший уровень характеризуется тем, что геометрические фигуры рассматриваются как целые и различают­ся только по своей форме. Если показать дошкольнику круг, квад­рат, прямоугольник и сообщить ему соответствующие названия, то после некоторого времени он сможет безошибочно распозна­вать эти фигуры исключительно по их форме (причем еще не ана­лизированной), не отличая квадрат от прямоугольника. На этом уровне квадрат противопоставляется прямоугольнику.

На следующем, втором уровне проводится анализ восприни­маемых форм, в результате которого выявляются их свойства. Геометрические фигуры выступают уже как носители своих свойств и распознаются по этим свойствам, свойства фигур ло-гически еще не упорядочены, они устанавливаются эмпириче­ским путем. Сами фигуры также не упорядочены, так как они только описываются, но не определяются. Этот уровень мышле­ния в области геометрии еще не включает структуру логического следования.

Описанные выше два уровня вполне доступны детям 4—6 лет, и это обстоятельство следует учитывать при составлении про­грамм обучения и разработке методики.

Из чего состоит геометрическая фигура?

Всякая геометрическая фигура подразумевается состоящей из точек, т.е. всякая геометрическая фигура представляет собой множество точек, в том числе одну точку тоже принято считать геометрической фигурой.

На предматематическом уровне дети знакомятся с простейши­ми, но наиболее распространенными геометрическими фигурами: различными линиями, формами блоков — квадратом, кругом, треугольником, а также пятиугольником, шестиугольником. Строгих определений, разумеется, на этом уровне не дается.

Виды геометрических фигур

Будем рассматривать далее лишь те виды простейших геомет­рических фигур, с которыми приходится иметь дело в процессе обучения дошкольников.

Все геометрические фигуры делятся на плоские и пространст­венные. Так, например, квадрат, круг — плоские фигуры; куб, шар — пространственные. Начнем с рассмотрения линий. Под линией будем иметь в виду плоскую линию — линию, все точки которой лежат на некоторой плоскости, а сама линия есть под­множество точек плоскости.

Прямую линию, или просто прямую, можно выделить среди других линий с помощью ее характеристических свойств, т. е.

таких свойств, которыми обладает только прямая и никакие дру­гие линии.

На илл. 8 между деревом и домом проложено несколько тро­пинок. На геометрическом языке это означает: через две точки D и С проходит несколько линий. Прямая выделяется среди них тем, что это — линия кратчайшего расстояния.

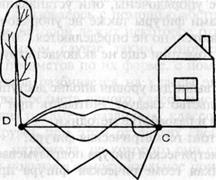
Еще одно характеристическое свойство прямой: через две точки D и С можно провести много различных линий, прямых — только одну, т. е. через две точки проходит одна и только одна прямая.

Линии бывают замкнутыми и незамкнутыми. Например, пря­мая — незамкнутая линия, окружность — замкнутая.

По отношению к прямой две точки могут находиться «по одну сторону» от нее или «по разные стороны». Например, если дом и дерево находятся по одну сторону от речки, можно дойти от дома до дерева или обратно, не проходя через мост. Если же они нахо­дятся по разным сторонам от реки, то дойти от дома до сада или обратно, не проходя через мост, нельзя.

На геометрическом языке эта ситуация описывается следу­ющим образом. Две точки А и В находятся по одну сторону от прямой /, если отрезок, соединяющий эти точки, не пересекает прямую / (илл. 9).

Первые представления о внутри и вне закрепляются в играх с обручами, когда дети встречаются со все усложняющимися ситуа­циями: определение блоков внутри и вне одного обруча, внутри одного и вне другого обруча, внутри всех трех обручей, внутри двух обручей и вне третьего и т. п. Поэтому перед решением задач, связанных с классификацией блоков или фигур в играх с обруча­ми, необходимо выяснить, распознают ли дети внутреннюю и внешнюю области по отношению к каждому обручу.

Дата добавления: 2015-04-24