М. Н. Полякова, А. М. Вербенец 6 страница

Переведем теперь эти ситуации на язык геометрии.

Интуитивно ясно, что всякая окружность разбивает множест­во всех не принадлежащих ей точек плоскости на две области (илл. 10). Если две точки А и В или D и Е лежат в одной области, то отрезок, соединяющий их, не пересекает линии /; если две точки, например С и D, принадлежат различным областям, то со­единяющий их отрезок пересекает линию / (в точке К).

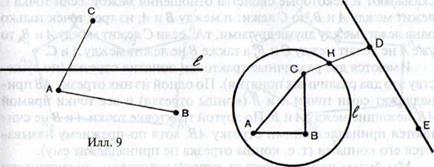
Илл. 10

Одна из этих областей называется внутренней, другая — внеш­ней. Каким же геометрическим свойством можно охарактеризо­вать внутреннюю или внешнюю область?

Область, которая интуитивно принимается за внешнюю, обла­дает следующим свойством: можно найти в этой области две точ­ки, например D и Е, такие, что прямая, проходящая через них, целиком лежит в этой области. Вторая область, которая интуитивно принимается за внутреннюю, не обладает этим свойством или характеризуется свойством, представляющим собой отрицание ха­рактеристического свойства внешней области, т. е. нельзя найти в ней такие две точки, чтобы прямая, проходящая через них, лежала целиком в этой области (или, иначе, прямая, проходящая через любые две точки этой области, обязательно пересекает линию /)-

Выше мы пользовались понятием отрезок и связывали его не­изменно с двумя точками: «отрезок АВ», «отрезок, соединяющий точки А и В» и т. п. Что же такое отрезок? Иногда говорят «часть прямой». Это можно понимать как подмножество точек прямой. Но какое это подмножество?

Иногда пользуются отношением между, применимым к трем точкам. Это отношение соответствует наглядному представлению о точке, лежащей на прямой между двумя другими точками: если точка С лежит между точками А и В, то нельзя «дойти» по прямой от А к В, не пройдя через точку С. Эти наглядные представления под­сказывают и некоторые свойства отношения между: если точка С лежит между А и В, то С лежит и между В и А; из трех точек только одна лежит между двумя другими, т. е. если Слежит между А и В, то уже А не лежит между Си В, а также В не лежит между А и С.

Имеются две различные трактовки понятия отрезка (по суще­ству это два различных понятия). По одной из них отрезку АВ при­надлежат сами точки А я В (концы отрезка) и все точки прямой АВ, лежащие между А и В. По другой трактовке точки А и В не счи­таются принадлежащими отрезку АВ, хотя по-прежнему называ­ются его концами (т. е. концы отрезка не принадлежат ему).

Мы будем придерживаться первой трактовки, дидактически более целесообразной.

Так как через две точки А и В проходит единственная прямая АВ, то эти две точки определяют и единственный отрезок с кон­цами А я В.

Зная, что такое отрезок, можно уточнить и понятие ломаной линии.

Если А\,А₂, At,,.., A„-j, А_п — точки, никакие последовательные три из которых не лежат на одной прямой, то линия, состоящая из отрезков/41Л2>^2^3>..,А_п_]А„, называется ломаной линией, эти отрез­ки называются звеньями ломаной, а точки А\, А₂, A3,.., А_п_], А„ — ее вершинами; точки А\ я А_п называются также концами ломаной Если концы ломаной совпадают, то ломаная называется замк­нутой, в противном случае — незамкнутой (строгие определения замкнутой и незамкнутой кривой линии в элементарной геомет­рии не даются).

На илл. 11, А изображена замкнутая ломаная линия, на илл. 11, 2> — незамкнутая.

Как и всякая замкнутая линия, замкнутая ломаная линия раз­бивает множество не принадлежащих ей точек плоскости на две области — внутреннюю и внешнюю.

Среди ломаных линий выделяют простые (без самопересече­ний) ломаные линии, т. е. такие, которые сами себя не пересекают.

Изображенные на илл. 11 ломаные линии простые. На илл. 12 изображены непростые, сами себя пересекающие ломаные линии.

Перейдем теперь к рассмотрению многоугольников. Имеются два основных подхода, по существу определяющих различные понятия: согласно одному из них, под многоугольником понимают простую замкнутую ломаную линию, согласно второму — простую замкнутую ломаную вместе с ее внутренней областью или объеди­нение простой замкнутой ломаной и ее внутренней области.

Согласно первой трактовке, модель многоугольника, напри­мер, можно изготовить из проволоки, по второй — вырезать из бу­маги. Какая же из двух трактовок более целесообразна с дидакти­ческой точки зрения? (С логической точки зрения обе трактовки корректны и имеют право на существование.) Для маленьких детей более естественным является называть квадратом, треугольником и т. д. именно ту фигуру, которую они закрасили и вырезали, т. е. ло­маную вместе с ее внутренней областью. Поэтому представляется, что и для школы вторая трактовка является более целесообразной.

Многоугольники классифицируются по числу сторон или углов: треугольники, четырехугольники, пятиугольники, шести­угольники и т.д. Наблюдая различные многоугольники, можно обнаружить наличие или отсутствие свойства, называемого выпук­лостью.

На илл. 13 изображены многоугольники, обладающие (в случа­ях/1, Б, Г, Е) и не обладающие (в случаях В, Д, Ж) этим свойством.

Как же геометрически описать это интуитивно ясное свойст­во? Любой из многоугольников в случаях Л, Б, Г, Е расположен по одну сторону от прямой, проведенной через каждую его сторону, т. е., если продолжить любую сторону, полученная прямая не пере­сечет многоугольник (с этой целью на рисунке стороны этих многоугольников продолжены пунктиром). В каждом из много­угольников в случаях В, Д, Ж существует хотя бы одна такая сто­рона, продолжение которой пересекает многоугольник. Первые называются выпуклыми, вторые — невыпуклыми.

Треугольник, квадрат, прямоугольник — выпуклые четырех­угольники. Пятиконечная звездочка — невыпуклый десятиуголь­ник.

Стороны и вершины многоугольника, т. е. замкнутая лома­ная, образуют границу многоугольника. Это интуитивно ясное понятие. Например, интуитивное представление о границе фи­гуры готовит детей к географическому понятию границы.

Чем же отличается граничная точка, т. е. точка, принадлежа­щая границе, от внутренней точки многоугольника (и вообще фи­гуры)? Как это различие описать геометрически?

С этой целью введем понятие окрестности точки. Под окрест­ностью точки А будем понимать круг любого радиуса с центром в точке А. Теперь, пользуясь этим весьма наглядным понятием, опи­шем различие между внутренней и граничной точками многоуголь­ника.

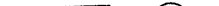Для любой внутренней точки А, как бы близка она ни была к границе, всегда можно найти окрестность, все точки которой внутренние (илл. 14).

Для граничной точки В нет такой окрестности, т. е., какую бы окрестность точки В ни взяли, внутри ее найдутся как внутренние, так и внешние точки. Такими же свойствами обладают внутрен­ние и граничные точки на географической карте, представляющей собой некоторую геометрическую фигуру.

Например, на географической карте России для любой внут­ренней точки можно найти окрестность, внутри которой все точки принадлежат территории России. Для любой точки на гра­нице России такой окрестности нет, т. е. в любой окрестности такой точки найдутся как точки, принадлежащие России, так и точки, принадлежащие соседнему государству.

Среди форм используемых нами блоков (или фигур) кроме тре­угольника, квадрата, прямоугольника имеется и круг. Кроме того, многие предметы, с которыми встречаются дети (тарелки, блюдца, колеса велосипеда и др.), имеют круглую форму. Считаем нецеле­сообразным для дошкольников вводить термин окружность.

В элементарной геометрии круг определяется как множество (или геометрическое место) всех точек плоскости, удаленных от некоторой точки, называемой центром, на расстояние, не превы­шающее R (R — радиус круга); окружность определяется анало­гично как множество всех точек плоскости, удаленных от точки, называемой центром, на одно и то же расстояние R.

Заметим, что если в этих формулировках слово «плоскость» за­менить словом «пространство», то получатся определения шара и сферы, соответственно, пространственных аналогов круга и окруж­ности.

Круг, окружность, шар и сферу можно определить и генетиче­ски, т. е. описанием процесса образования этих фигур. Этот про­цесс легко смоделировать: если отрезок зафиксировать в одном конце и вращать его около этого конца, то он опишет круг, а второй его конец — окружность. Если полукруг вращать около диаметра, то он опишет шар, а ограничивающая его полуокружность — сферу.

Дошкольники знакомятся также с одним из простейших многогранников, каким является куб.

Куб — пространственный аналог квадрата. Он ограничен шес­тью квадратами. Его можно сконструировать (склеить) из плоской фигуры — выкройки, изображенной на илл. 15

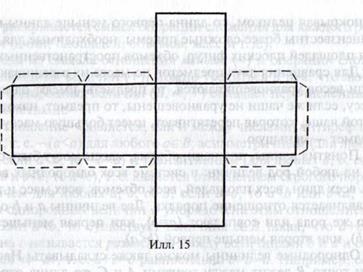
Ознакомление детей с описанными выше простейшими гео­метрическими фигурами является пропедевтической основой для дальнейшего формирования и развития у них геометрических, в том числе пространственных, представлений.

2.5. Величины и их измерение

Что такое величина

Величина — одно из основных математических понятий, воз­никшее в древности и подвергшееся в процессе длительного раз­вития ряду обобщений.

Общее понятие величины является непосредственным обоб­щением более конкретных понятий: длины, площади, объема, массы, скорости и т. п. Каждый конкретный род величин связан с определенным способом сравнения соответствующих свойств объектов. Например, в геометрии отрезки сравниваются при по­мощи наложения, и это сравнение приводит к понятию длины: два отрезка имеют одну и ту же длину, если при наложении они совпадают; если же один отрезок накладывается на часть другого не покрывая целиком, то длина первого меньше длины второго. Общеизвестны более сложные приемы, необходимые для сравне­ния площадей плоских фигур, объемов пространственных тел.

Для сравнения двух предметов по массе их взвешивают. Если чаши весов уравновешиваются, то предметы имеют одинаковую массу, если же чаши не уравновешены, то предмет, находящийся на той чаше, которая перетягивает, имеет большую массу, второй предмет — меньшую.

Понятия длины, площади, объема, массы могут быть обобще­ны на любой род величин: в системе всех однородных величин, т. е. всех длин, всех площадей, всех объемов, всех масс и т. д., ус­танавливается отношение порядка. Две величины а и Ь одного и того же рода или совпадают (а=Ь), или первая меньше второй (а<Ь), или вторая меньше первой (Ь<а).

Однородные величины можно также складывать. Например, если точка В лежит между точками А и С, то длина отрезка АС равна сумме длин отрезков АВ и ВС (илл. 16, А).

Если плоская фигура состоит из двух частей, не имеющих дру­гих общих точек, кроме граничных, то площадь S всей фигуры равна сумме площадей S1+S2 этих частей (илл. 16, Б).

Если предмет состоит из двух частей, то его масса т равна сумме m\+ni2 масс т\ыгп2 этих частей.

Если пространственная фигура состоит из двух частей, все общие точки которых образуют их общую границу, то объем всей пространственной фигуры равен сумме 1+2 объемов Щ и i этих частей (илл. 16, В).

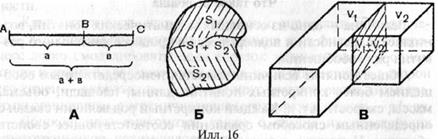
Так раскрывается смысл операции сложения для каждого рода величин (длин, площадей, объемов, масс и т.д.).

Исходя из смысла отношения меньше (<) и операции сложе­ния однородных величин (+), можно убедиться в том, что любая система однородных величин (В, <, +) обладает перечисленными ниже свойствами.

1) Отношение < является, как и между числами, антирефлек­сивным, т. е. -i(o<a) для любого ае В; асимметричным (для любых а, аеВ, если а<Ь, то -*Ь<а) и транзитивным (для любых а, Ь, се В, если а<Ь и Ь<с, то а<с), т. е. является отношением строгого поряд­ка. Причем для любых а, Ь, се В, если а*Ь, то а<Ь или Ь<а, т. е. система однородных величин В упорядочена этим отношением.

2) Если а<Ь, то существует величина се В такая, что а+с=Ь. Величина с называется разностью между величинами b и а и обо­значается «b—а», т. е. а+с=Ь равносильно с—Ъ—а. Например, если взять два отрезка, АВ длины а и CD длины Ъ, причем а<Ь, и отло­жить на отрезке CD отрезок СВ[, равный АВ, то образовавшийся отрезок B\D будет иметь длину c—b-а (илл. 17).

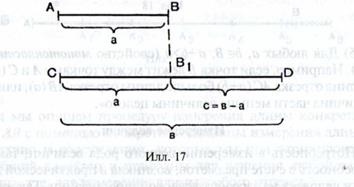
3) Сложение величин, как и сложение чисел, обладает свойст­вом переместительности (коммутативности): a+b=b+a для любых я, be В.

Например, безразлично — присоединить к отрезку АВ длины а отрезок ВС длины b или наоборот — мы все равно получим в результате один и тот же отрезок.

4) Сложение величин обладает свойством сочетательности (ассоциативности):

a+(b+c)=(a+b)+c для любых а, Ь, се В.

Например, если присоединить к отрезку АВ длины а отрезок BD длины Ь+с так, чтобы точка В лежала между точками А и D (илл. 18), то получим отрезок AD длины а+ф+с); если к отрезку АС длины а+b присоединить отрезок CD длины с, то получим от­резок AD, длина которого выражается через (а+Ь)+с; но так как мы получили один и тот же отрезок AD, то a+(b+c)=(a+b)+c. По­этому можно писать без скобок а+Ь+с.

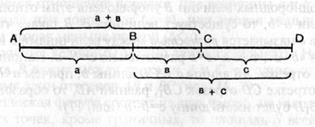
Илл. 18

5) Для любых a, be В, а+Ь>а (свойство монотонности сложе­ния). Например, если точка Я лежит между точками А и С (илл. 18), то длина отрезка АС (а+b) больше длины отрезка АВ (а), или вообще «величина части меньше величины целого».

Измерение величин

Потребность в измерении всякого рода величин, так же как потребность в счете предметов, возникла в практической деятель­ности человека на заре человеческой цивилизации. Так же как для определения численности множеств, люди сравнивали различные множества, различные однородные величины, определяя прежде всего, какая из сравниваемых величин больше, какая меньше. Эти сравнения еще не были измерениями. В дальнейшем процедура сравнения величин была усовершенствована. Одна какая-нибудь величина принималась за эталон, а другие величины того же рода

(длины, площади, объемы, массы и т.п.) сравнивались с этало­ном. Когда же люди овладели знаниями о числах и их свойствах, величине-эталону приписывалось число 1 и этот эталон стал на­зываться единицей измерения. Цель измерения стала более опре­деленной — оценить, сколько единиц содержится в измеряемой величине. Результат измерения стал выражаться числом.

Задача измерения величин, так же как и задача определения численности множеств предметов, является источником, порож­дающим числа. Однако в отличие от первой задачи, решение ко­торой полностью обеспечивается натуральными числами, для за­дачи измерения величин этих чисел недостаточно. Это наглядно обнаруживается описанием процедуры измерения на простейшем примере измерения длин.

Пусть необходимо измерить длину отрезка АВ с помощью еди­ницы измерения CD длины е (илл. 19).

Хотя мы опишем процедуру измерения длины конкретного отрезка АВ с помощью конкретной единицы измерения длины е, все действия и рассуждения, которые мы при этом проведем, носят общий характер и пригодны для решения любой задачи этого типа, т. е. для измерения длины любого отрезка.

Откладываем отрезок CD от точки А последовательно на отрез­ке АВ, при этом возможны следующие случаи.

1. Возможно, что отрезок CD отложится на отрезке АВ целое число раз. На илл. 19, А, например, 5 раз (а вообще п раз), т.е. второй конец отрезка CD (точка D) при пятом (а в общем случае при п-м) отложении совпадает с точкой В (концом отрезка АВ).

Так как длина отрезка АВ равна 5е (пе), то, принимая длину е за 1, можно считать числовое значение длины отрезка АВ равным 5 (в общем случае — я).

Если обозначить числовое значение длины отрезка АВ через \АВ\ (в дальнейшем для краткости вместо «числовое значение длины» будем говорить просто «длина» там, где это не приводит к недоразумению), то в нашем примере |/4i?|=5, а в общем случае \АВ\=п. В этом случае натуральные числа обеспечивают решение задачи измерения.

2. Возможно, что точка А$ (А„) не совпадает с точкой В (илл. 19, Б), причем |Л5.В|<е, т. е. если отложить еще один раз от­резок CD, то конец его Аь(А_п+1) уже окажется вне отрезка АВ, иными словами, точка В окажется между точками А5 и Аь (А_п и A„+i). Тогда длина отрезка АВ уже не выражается натуральным числом, она находится «между» двумя последовательными нату­ральными числами 5<\АВ\<6, или в общем виде п<\АВ\<п+\, между которыми, как известно, нет других натуральных чисел.

В этом случае мы можем лишь приближенно считать длину отрезка АВ равной одному из этих чисел, 5 или 6 (я или п+1). В ре­зультате получаем приближенное значение измеряемой длины с точностью до 1. Это означает, что, принимая одно из этих чисел за значение длины отрезка АВ, мы допускаем погрешность, мень­шую 1, причем число 5 (я) — приближенное значение длины с недостатком, а число 6 (я+1) — с избытком. Если точка В ближе к точке А^ (А„), то число 5 (я) ближе к истинному (точному) значе­нию длины отрезка АВ, если же точка В ближе к точке А^ (А„+\), то число 6 (я+1) ближе к точному значению этой длины. В зави­симости от этого выбирают то приближенное значение, которое ближе к точному, что дает меньшую погрешность.

Если такая степень точности удовлетворяет нас, то можно счи­тать процесс измерения законченным. Однако практика часто предъявляет требование получить результаты измерений с более высокой степенью точности, т. е. с меньшей погрешностью.

С этой целью возникает необходимость продолжить процесс измерения, т. е. измерить длину остатка, отрезка Аф, в общем слу­чае А_пВ. Естественно, это нельзя сделать с помощью той же еди­ницы измерения CD, которая не умещается на этом отрезке. Надо выбрать более мелкую единицу измерения, какую-то часть отрез­ка CD, допустим десятую. Тогда длина е\ этой новой единицы из­мерения равна 0,1е, т.е. числу 0,1 (здесь неявно применяется свойство о возможности деления величины на какое угодно число частей).

Далее процедура измерения повторяется, но уже примени­тельно к отрезку Аф (А_пВ) и с единицей измерения длины 0,1. Значит, опять возможны два случая:

1) Новая единица измерения уместится на отрезке Аф (А„В) целое число раз, например 3 раза, а вообще п_{ раз, где «i< 10, так как прежняя единица измерения е не умещается на отрезке А„В. В этом случае И-#1⁼5,3 (\АВ\=п, п{), т.е. для выражения числового значения длины уже потребовалось дробное число (мы взяли де­сятую долю первой единицы в качестве второй единицы измере­ния, чтобы можно было воспользоваться десятичными дробями).

2) Новая единица измерения не належится целое число раз, т. е. точка В не совпадает с концом накладываемой единицы изме­рения. В этом случае получаем, например, 5,3<|А8|<5,4, или в общем виде п, п\<\АВ\<п, п{, где п{=п\ + \, т.е. каждое из чисел 5,3 и 5,4 («, п\ и п, п{) выражает приближенное значение длины отрезка АВ, первое — с недостатком, второе — с избытком, и оба — с точностью до 0,1. Принимая любое из этих чисел за длину отрезка АВ, мы допускаем погрешность, меньшую 0,1, а следова­тельно, в десять раз меньшую, чем та, которая получается, если принимать за приближенное значение длины этого отрезка нату­ральное число 5 или 6.

Если такая точность удовлетворительна, то процесс измере­ния можно считать законченным. В противном случае процесс продолжается, т. е. повторяется та же процедура, но уже примени­тельно к новому остатку, отрезку А^^В, и с новой единицей наме­рения, длина которой, например, десятая доля прежней единицы, т.е. ^2=0,01. Заметим, что можно было бы принимать 61=72 е, ^e2~^xh ^еь ^и тогда были бы получены приближенные значения длины в виде двоичных дробей.

В результате получаем, например, либо \АВ\=5,36 (]АВ\=п, п\п2), либо 5,36<|Аб|<5,37 (п, п\п2<\АВ\<п, п\п{~), т.е. приближен­ные значения длины: 5,36 (п, n\ni) с недостатком, или 5,37(и, /Ji«₂') с избытком, но уже с точностью до 0,01 или с погрешностью, в 100 раз меньшей, чем первые приближения с помощью натураль­ных чисел 5 или 6.

Если такая точность достаточна для решаемой задачи, то про­цесс измерения считается законченным, в противном случае он продолжается, т. е. процедура измерения повторяется примени­тельно к новому остатку и с новой единицей измерения.

Естественно возникает вопрос: до каких пор может продол­жаться процесс измерения?

Оказывается, вообще возможны два случая: 1) на каком-то этапе процесса измерения единица измерения уложится целое число раз на измеряемом отрезке; 2) ни на каком этапе процесса измерения это не случится и, следовательно, процесс измерения будет продолжаться бесконечно.

Последнее обстоятельство означает, что существуют так на­зываемые несоизмеримые отрезки, например диагональ квадра­та и его сторона. Если измерять диагональ квадрата стороной, т. е. принимая сторону квадрата за единицу измерения, то про­цесс измерения никогда не закончится, так как ни сама сторона квадрата, им любая ее часть, полученная от деления стороны на целое число равных частей, не укладывается целое число раз в диагонали этого квадрата. В этом случае и рациональных чисел, т. е. целых и дробных, недостаточно для решения задачи изме­рения. В математике этот пробел устраняется дальнейшим рас­ширением системы чисел с помощью введения иррациональных чисел. Как Как известно из школьной математики, иррациональные числа представляются в виде бесконечных десятичных неперио­дических дробей и образуют, таким образом, вместе с рацио­нальными числами множество вещественных (или действитель­ных) чисел, т. е. объединение множеств рациональных и ирра­циональных чисел.

Однако только теоретически процесс измерения может ока­заться бесконечным. Практически же процесс измерения длин (и других величин) состоит из конечного числа шагов, что дает в ре­зультате приближенное значение измеряемой величины с любой требуемой степенью точности, зависящей от количества выпол­ненных шагов в процессе измерения.

2.6. Алгоритмы

Что такое алгоритм

Воспитание детей с самого рождения, в частности воспитание дошкольников, включает усвоение ими разного рода правил и их строгое выполнение (правила утреннего туалета, одевания и раз­девания, принятия пищи, перехода улицы и др.). Режим дня до­школьника представляет собой систему предписаний о выполне­нии детьми и воспитателем действий в определенной последова­тельности. Обучая детей счету, измерению длин, сложению и вычитанию чисел, уборке комнаты, посадке растений и т. д., мы сообщаем им необходимые правила о том, что и в какой последо­вательности нужно делать для выполнения задания. Организовы­вая разнообразные дидактические и подвижные игры, мы знако­мим дошкольников с их правилами.

О всех видах деятельности, осуществляемых по определенным предписаниям, говорят, что они выполняются по определенным алгоритмам. С малых лет человек усваивает и исполняет в каждо­дневной жизни большое число алгоритмов, часто даже не зная, что это такое.

Что такое алгоритм? Нередко встречаются виды однотипных задач, например: сложение двух многозначных чисел; переход улицы, регулируемый или нерегулируемый светофором; измерение длины отрезка и т. д. Естественно возникает вопрос: существует ли достаточно общий способ, который можно было бы использовать для решения любой задачи данного вида однотипных задач?

Если такой общий способ существует, то его называют алго­ритмом^ данного вида задач. Для каждого из приведенных выше видов задач имеется соответствующий алгоритм.

1 Слово алгоритм происходит от имени известного математика IX в. аль-Хорезми, что означает «из Хорезма», впервые сформулировавшего правила выполнения арифметических действий над многозначными числами. Через труды аль-Хорезми в Европу проникли спосо­бы действий с числами в десятичной системе счисления, которые стали называть алгоритма­ми согласно латинской транскрипции имени ученого. В течение столетий значение слова «алгоритм» постепенно обобщалось, и сегодня под алгоритмом понимают некоторый общий метод или способ, предписание, инструкцию, свод правил для решения за конечное число шагов любой задачи из определенного вида однотипных задач, для которого предназначен этот метод.

Для задачи сложения двух многозначных чисел известен спо­соб сложения «в столбик», пригодный для сложения любых двух многозначных чисел, т. е. для решения любой частной задачи из этого вида однотипных задач.

Для задачи перехода улицы, например нерегулируемого свето­фором, можно сформулировать общий способ в виде следующего предписания, состоящего из 10 указаний, или команд:

1. Подойди к краю тротуара у знака перехода.

2. Стой.

3. Смотри налево.

4. Если идет транспорт слева, то перейди к указанию 2, иначе — к указанию 5.

5. Пройди до середины улицы.

6. Стой.

7. Смотри направо.

8. Если идет транспорт справа, то перейди к указанию 6, иначе — к указанию 9.

9. Пройди вторую половину улицы до противоположного тро­туара.

10. Переход улицы закончен.

Интуитивно под алгоритмом понимают общепонятное и точ­ное предписание о том, какие действия и в каком порядке необ­ходимо выполнить для решения любой задачи из данного вида однотипных задач.

Это определение, разумеется, не является математическим оп­ределением в строгом смысле, так как в нем встречается много терминов, смысл которых хотя и интуитивно может быть ясен, но точно не определен («предписание», «общепонятное», «точное», «действие»). Однако оно представляет собой разъяснение того, что обычно вкладывается в интуитивное понятие алгоритма, а для наших целей этого вполне достаточно.

Какие же свойства характеризуют всякий алгоритм?

Анализ различных алгоритмов позволяет выделить следующие общие свойства, присущие алгоритмам:

а) массовость, т. е. алгоритм предназначен для решения не од­ной какой-нибудь задачи, а для решения любой задачи из данного вида однотипных задач;

б) определенность (или детерминированность), т. е. алгоритм
представляет собой строго определенную последовательность
шагов, или действий, он однозначно определяет первый шаг и
каждый следующий шаг, не оставляя решающему задачу никакой
свободы выбора следующего шага по своему усмотрению;

в) результативность: решая любую задачу из данного вида
задач по соответствующему алгоритму, мы за конечное число
шагов получаем результат. Разумеется, для различных частных
задач одного вида число шагов может оказаться различным, но
оно всегда конечно.

Алгоритм — одно из фундаментальных научных понятий, ис­пользуемое и математикой, и информатикой — наукой, изучающей способы представления, хранения и преобразования информации с помощью различных автоматических устройств. Наличие алго­ритма для осуществления некоторой деятельности является необ­ходимым условием передачи этого вида деятельности различным автоматическим устройствам, роботам, компьютерам (от отпуска стакана газированной воды, продажи авиабилета с хранением и преобразованием информации о наличии свободных мест до уп­равления сложными технологическими процессами, не говоря уже о выполнении огромных объемов вычислительной работы, связан­ной с решением сложных научно-технических задач).

Имеются различные формы записи или представления алго­ритмов, предназначенные для различных исполнителей: словес­ные предписания, в том числе включающие различные формулы; наглядные блок-схемы, ориентированные на исполнителя-чело­века; программы, представляющие собой запись алгоритма на языке, понятном ЭВМ, т. е. языке программирования.

Здесь уместно уточнить, что означает выдвинутое требование «общепонятности» предписания, которым задается алгоритм. Это означает, что предписание должно быть сформулировано так, чтобы оно было одинаково понятно всем исполнителям той кате­гории, на которую оно ориентировано. Это имеет чрезвычайно важное значение, в частности, при обучении маленьких детей. На­пример, приведенные выше предписания, задающие алгоритмы перехода улицы и измерения длины, не предназначены для обуче­ния дошкольников. Для этой цели нужно сформулировать их на понятном детям языке, что и делает любой воспитатель, если, раз­умеется, он имеет соответствующую подготовку и понимает свои задачи.

Однако приведенные выше предписания составлены так, что они выявляют шаговую (дискретную) оперативно-логическую структуру алгоритмов. Поясним, что это означает.

1. Каждый алгоритм может быть представлен в виде последо-
вательности шагов. Разумеется, понятие шаг является относитель-
ным. Один и тот же алгоритм можно по-разному представить в
виде последовательности шагов, и не всегда отдельные шаги соот-
ветствуют элементарным действиям. Само понятие элементарное
действие относительно: одно и то же действие может быть для
одного ребенка, и не только ребенка, элементарным, для друго-
го — неэлементарным (в результате чего и возникает необходи-
мость в расчленении этого действия на другие, элементарные,
действия).

Дата добавления: 2015-04-24