Этапы построения математической модели

При построении математической модели системы можно выделить несколько этапов (рис. 2.1):

I -й этап. Постановка задачи. Этапу предшествует возникновение ситуаций или проблем, осознание которых приводит к мысли
их обобщения или решения для последующего достижения, какого-
либо эффекта. Исходя из этого, объект описывается, отмечаются
вопросы, подлежащие решению, и ставится цель исследования. Здесь необходимо уяснить, что мы хотим получить в результате исследований. Предварительно нужно оценить, нельзя ли получить эти
результаты другим, более дешевым или доступным путем.

I. Постановка задачи

II. Определение задачи

III. Составление математической модели задачи

IV. Вычисления. Эксперимент.

V. Выдача результатов

Рис. (2.1.) Последовательность процесса моделирования

II-й этап. Определение задачи. Исследователь старается определить, к какому виду относится объект, описывает параметры
состояния объекта, переменные, характеристики, факторы внешней среды. Необходимо познать закономерности внутренней организации объекта, очертить границы объекта, построить его структуру. Эта работа называется идентификацией системы. Отсюда
выбирается задача исследования, которая может решать вопросы:
оптимизации, сравнения, оценки, прогноза, анализа чувствительности, выявления функциональных соотношений и т.п.

Следующая работа связана, с разработкой концептуальной мо-
дели. Например, для создания системы очистки воды концептуальная модель системы приведена на рис. (2.2.).

Концептуальная модель позволяет оценить положение системы
во внешней среде, выявить необходимые ресурсы для ее функционирования, влияние факторов внешней среды и то, что мы ожидаем
на выходе.

Необходимость проведения исследования возникает из реальных
ситуаций, складывающихся в процессе работы системы, когда они в чем-либо начинают не удовлетворять каким-либо старым или новым
требованиям. Если недостатки очевидны и известны методы их уст-
ранения, то нет необходимости в исследованиях.

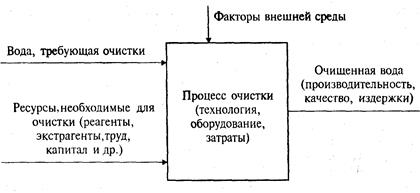
Рис (2.2.) Схема концептуальной модели системы очистки.

К сожалению, такая ситуация встречается достаточно редко. В
силу сложности систем и достаточно большого числа факторов, влияющих на эффективность их действия, поставить «диагноз» системе не всегда просто. Изучение сложившейся ситуации, поведения
системы и ее элементов, опыт исследователя и его интуиция позволяют поставить предварительный «диагноз» системе, определить и
сформулировать задачу исследования.

Исходя из задачи исследования, можно определить назначение
математической модели, которая должна быть построена для исследования. Такие модели могут решать задачи:

• выявления функциональных соотношений, заключающихся в
определении количественных зависимостей между входными фактора-
ми модели и выходными характеристиками исследуемого объекта;

• анализа чувствительности, заключающегося в установлении
факторов, которые в большей степени влияют на интересующие ис-
следователя выходные характеристики системы;

• прогноза — оценки поведения системы при некотором предполагаемом сочетании внешних условий;

• оценки — определения, насколько хорошо исследуемый объект
будет соответствовать некоторым критериям;

• сравнения, заключающегося в сопоставлении ограниченного
числа альтернативных вариантов систем или же в сопоставлении
нескольких предлагаемых принципов или методов действия;

• оптимизации, состоящей в точном определении такого сочетания переменных управления, при которых обеспечивается экстремальное значение целевой функции.

Выбор задачи определяет процесс создания и экспериментальной проверки модели.

Любое исследование должно начинаться с построения плана, включающего обследование системы и анализ ее функционирования. В
плане должны быть предусмотрены:

• описание функций, реализуемых объектом;
• определение взаимодействий всех систем и элементов объекта;

• определение зависимости между входными и выходными переменными и влияние переменных управляющих воздействий на
эти зависимости;

• определение экономических показателей функционирования
системы.

Результаты обследования системы и окружающей среды представляются в виде описания процесса функционирования, которое
используется для идентификации системы. Идентифицировать систему — значит выявить и изучить ее, а также:

получить более полную характеристику системы и ее поведения;

познать объективные закономерности ее внутренней организации;

очертить ее границы;
указать на вход, процесс и выход;
определить ограничения на них;
построить ее структурную и математическую модели;
описать ее на каком-либо формальном абстрактном языке;

определить цели, принуждающие связи, критерии действия системы.

После идентификации системы строится концептуальная модель,
являющаяся «идеологической» основой будущей математической
модели. Именно в ней отражается состав критериев оптимальности
и ограничений, определяющих целевую направленность модели. Перевод, на этапе формализации качественных зависимостей в количественные, преобразует критерий оптимальности в целевую функцию, ограничения — в уравнения связи, концептуальную модель-
в математическую модель.

Если посмотреть на схему построения математической модели
(см. рис. (2.1.), то можно увидеть, что процесс ее построения представляет собой не только прямую, но и обратную связь отдельных
этапов. Это означает, что при работе над последующим этапом приходится возвращаться к предыдущим для уточнения тех или иных моментов.

Рис. (2.3.) Факторная модель производственной системы очистки воды.

На основе концептуальной модели можно построить факторную модель (рис. (2.3.), которая устанавливает логическую связь между параметрами объекта, входными и выходными переменными, факторами внешней среды и параметрами управления, а также учитывать обратные связи в системе.

III-й этап. Составление математической модели. Вид математической модели в значительной степени зависит от цели исследования. Вначале лучше поискать подходящую модель в литературе или
использовать те или иные известные закономерности экологии в
виде функций, связывающих переменные и постоянные факторы
модели между собой.

Математическая модель может быть в виде математического
выражения, представляющего собой алгебраическое уравнение, или
неравенство, не имеющее разветвления вычислительного процесса при определении любых переменных состояния модели, целевой функции и уравнений связи.

Для построения такой модели формулируются следующие понятия:

• критерий оптимальности — показатель, выбираемый исследователем, имеющий, как правило, экологический смысл, который служит для формализации конкретной цели управления объектом ис-
следования и выражаемый при помощи целевой функции;

• целевая функция — характеристика объекта, установленная из
условия дальнейшего поиска критерия оптимальности, математически связывающая между собой те или иные факторы объекта
исследования. Целевая функция и критерий оптимальности — разные понятия. Они могут быть описаны функциями одного и того
же вида или же разными функциями;

• ограничения — пределы, сужающие область осуществимых,
приемлемых или допустимых решений и фиксирующие основные
внутренние и внешние свойства объекта. Ограничения определяют
область исследования, протекания процессов, пределы изменения
параметров и факторов объекта.

Так, например, для факторной модели, приведенной на рис. 1.5,
выбираем в качестве критерия оптимальности максимальный объем
очищенной воды при заданных ресурсах Х₁,Х₂,...,Х_n. Тогда целевая
функция должна связать между собой Х, А, S, F, т.е.

Y = max f (Х, А, S, F )

при ограничении значений переменных Х, Р _y и Q_об.

Дата добавления: 2015-04-24