Жесткие задачи

Некоторые обыкновенные дифференциальные уравнения (ДУ) не решаются ни одним из рассмотренных методов. Чтобы понять, почему это так, рассмотрим структуру ДУ. В общем случае ДУ n-го порядка имеют n постоянных времени. Если одна из постоянных времени достаточно мала по сравнению с шагом интегрирования, то задача называется жесткой и ее трудно решить обычными методами. В таких случаях шаг должен быть достаточно мал, чтобы можно было учитывать изменения наиболее быстроизменяющихся членов уравнения. В противном случае решение становится неустойчивым. Если величина шага очень мала по сравнению с интервалом, на котором отыскивается решение, то для получения решения потребуется очень много времени. А накапливающиеся в процессе длительных вычислений погрешности округления могут привести к получению бессмысленного результата. Рассмотрим, например, систему:

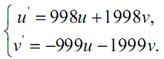
Если u(0) = v(0) =1, то решением будут (рис.3.7):

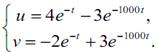
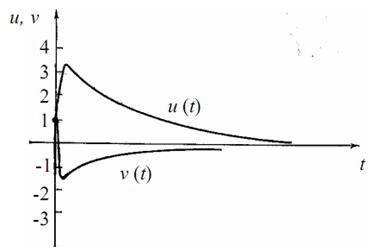
Рис. 3.7. Решение системы уравнений

После очень небольшого промежутка времени решение весьма близко к фун-кциям:

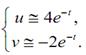
Предположим, что мы должны решить эту систему посредством метода Эйлера. Дискретное решение можно записать формулой:

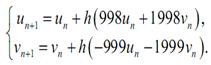
где u₀= v₀=1.

Если выбрать h = 0,02, то:

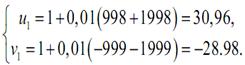
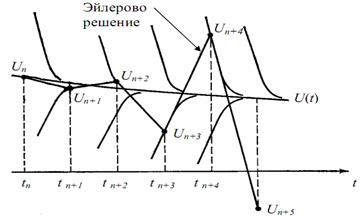
Рис.3.8. Семейство решений

Если сделать еще несколько шагов интегрирования, то результаты примут катастрофический характер. Это явление можно представить себе визуально, рассматривая семейство решений ассоциированных с u(t) (рис.3.8).

Переходная часть решения, которая, казалось бы, давно уже практически исчезла, тем не менее, мешает увеличить длину шага. Это особенно досадно, потому что на данном этапе вычислений решение очень гладко и, казалось бы, можно увеличить шаг.

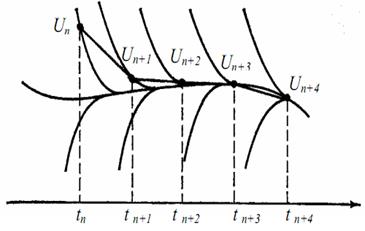
Рис.3.9. Работа неявного метода Эйлера

Большинство стандартных методов не приспособлено для решения жестких уравнений. Поэтому были изобретены специальные методы. Простейшим из них является так называемый неявный метод Эйлера, выражаемый формулой:

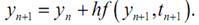
Работу неявного метода Эйлера покажем графически (рис.3.9).

Разработка эффективных методов для жестких уравнений является областью активных исследований.

назад

Дата добавления: 2015-04-24