Построение имитационных моделей динамических систем

Пример

Используя метод сосредоточенных масс, построить динамическую модель для анализа плавности хода автомобиля (рис. 4.1) [13]. В связи с неровностями дороги, движение автомобиля сопровождается колебаниями кузова и вибрациями его механизмов и деталей. Для того чтобы создать нормальные условия водителю и комфортные условия пассажирам, применяют упругую подвеску автомобиля. Эта подвеска содержит упругие элементы и амортизаторы. Динамическая модель колебательной системы автомобиля имеет следующий вид. В этой модели учитывается масса части кузова m₂, приходящаяся на колеса данного моста. Масса колес и моста m₁.

Коэффициент сопротивления диссипативных элементов подвески m₂ и шины m₁. С учетом наложенных позиционных связей на сосредоточенные массы m₁ и m₂, они могут перемещаться только вертикально вдоль осей соответственно z₁ и z₂.

Рис. 4.2. Динамическая модель плоских колебаний

Следовательно, система имеет две степени свободы. Внешние воздействия на эту систему создаются неровностями микро- и макро профиля дороги. Эти воздействия носят случайный характер и описываются случайными функциями q(t). Однако для более детального анализа влияния параметров подвески на колебания кузова необходимо учитывать связанность колебаний. В этом случае приходим к динамической модели плоских колебаний, в которой учитываются не только вертикальные колебания кузова относительно оси z0, но и угловые колебания b относительно оси y (рис.4.2).

Колебательная система имеет четыре степени свободы, и её состояние определяется фазовыми координатами z₀, b₂, z₁, z₂. Аналогичная модель используется при исследовании поперечных колебаний кузова.

В динамической системе, как правило, протекают процессы различной физической природы: механические, гидравлические, электрические, тепловые и т. д. Основой для построения структурной схемы такой системы служат физические законы. Они связывают между собой физические величины внутри системы и внешние силы. Основные уравнения динамической системы будем составлять с использованием понятия "динамические звенья", изучаемого в ТАР.

На первоначальном этапе составления структурной схемы связи между динамическими звеньями удобнее представлять в виде сети. Подобно структурным схемам, сети связей физических величин или просто сети связей используются для наглядного изображения физических зависимостей динамических систем. Между структурной схемой и сетью связей физических величин имеется прямое соотношение: прямоугольник структурной схемы соответствует ветви, а линия передачи сигнала - узлу сети [15]. Сравним структурную схему (рис.4.3) и сеть связей физических величин (рис.4.4) одной и той же системы.

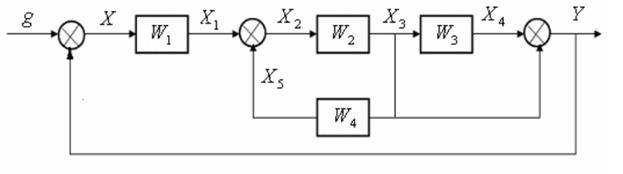
Рис.4.3. Структурная схема

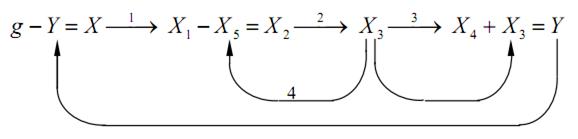
Рис. 4.4. Сеть связей физических величин

Правила составления сети связей физических величин:

1) номер ветви соответствует номеру передаточной функции динамического звена;

2) ветвь, соединяющая одноименные величины, не имеет номера (передаточная функция для такой ветви равна единице);

3) элементу сравнения на сети связей соответствует разность, а сумматору - сумма двух величин, равная третьей величине (результату);

4) результат вычитания или суммирования всегда записывают справа от знака равенства.

Используя принцип декомпозиции, можно любую сколь угодно сложную динамическую систему разделить на связанные между собой элементарные звенья. Рассмотрим некоторые элементарные звенья, их сети связей, физические зависимости между входными и выходными величинами, а также передаточные функции.

1) Редуктор (рис.4.5).

Рис.4.5 2) Пружина (рис. 4.6).

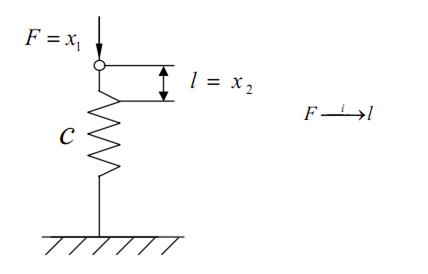
Рис. 4.6

3) Цилиндр (рис. 4.7).

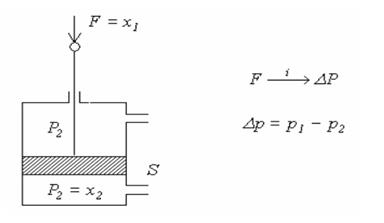
Рис. 4.7

4) Электрическое сопротивление (рис.4.8).

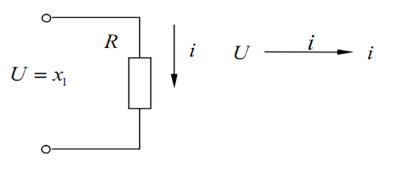
Рис. 4.8

5) Гидравлический дроссель (рис.4.9)

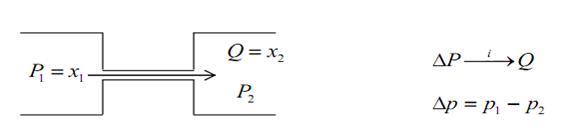
Рис.4.

6) Движущаяся масса (рис.4.10).

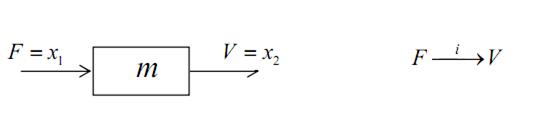
Рис. 4.10

7) Индуктивность (рис.4.11).

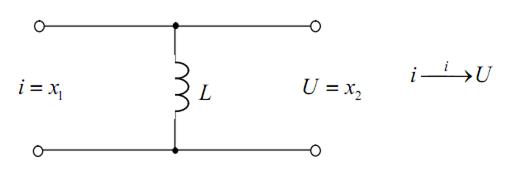
Рис. 4.11

8) Ёмкость (рис.4.12).

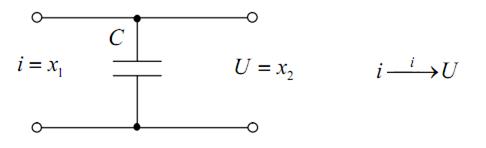
Рис. 4.12

9) Жидкостное трение (рис.4.13).

Рис. 4.13

10) Преобразование перемещения (рис.4.14).

Рис.4.14

Построив сеть связей и записав зависимости физических величин для каждого элементарного звена, нетрудно определить структурную схему и, если необходимо, передаточные функции динамической системы.

Дата добавления: 2015-04-24