
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Тема 3. Непрерывность. Равномерная непрерывность. Свойства непрерывных функций
|
|
|
|
Упражнения.
I. Используя определение Коши предела функции в точке, доказать следующие равенства.
1) 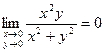 ; 2)
; 2) 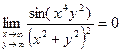 ; 3)
; 3)  ; 4)
; 4) 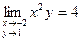 ; 5)
; 5)  .
.
II. Вычислить следующие пределы.
1)  ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  ;
;
5)  ; 6)
; 6)  ,
, 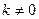 ; 7)
; 7)  ; 8)
; 8)  ;
;
9) 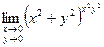 ; 10)
; 10)  ; 11)
; 11) 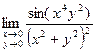 ; 12)
; 12) 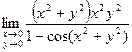 ;
;
13)  ; 14)
; 14)  ; 15)
; 15)  ;
;
16)  ; 17)
; 17) 
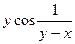 .
.
III. Для функции u найти  и ее повторные пределы
и ее повторные пределы 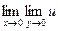 и
и 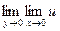 или доказать, что они не существуют.
или доказать, что они не существуют.
1)  ; 2)
; 2) 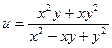 ; 3)
; 3) 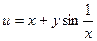 ; 4)
; 4) 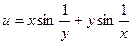 ; 5)
; 5)  .
.
IV. Найти предел функции 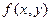 в точке (0, 0) по прямой
в точке (0, 0) по прямой  ,
, 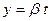 ,
,  ; доказать, что
; доказать, что 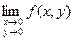 не существует.
не существует.
1)  ; 2)
; 2) 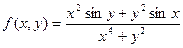 .
.
Функция f (x; y) называется непрерывной в точке M 0 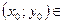 R 2, если:
R 2, если:
1) функция f определена в этой точке;
2) точка M 0 является предельной точкой D (f);
3) в точке M 0 существует конечный предел функции f, равный значению функции в этой точке, т.е.  .
.
На ε-δ языке последнее условие можно записать так
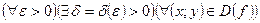

или, что тоже самое,
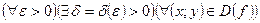
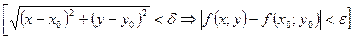 .
.
Для функций нескольких переменных справедливы теоремы о непрерывности суммы, произведения и частного функций, о сохранении знака непрерывной функцией, о непрерывности сложной функции, аналогичные соответствующими теоремами для функций из R 1 в R 1.
Точка 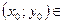 R 2, являющаяся предельной точкой области определения D (f) функции f (x; y), называется точкой разрыва этой функции, если выполняется хотя бы одно из следующих условий:
R 2, являющаяся предельной точкой области определения D (f) функции f (x; y), называется точкой разрыва этой функции, если выполняется хотя бы одно из следующих условий:
1) функция f не определена в точке 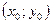 ;
;
2) точка M 0 не является предельной точкой D (f);
3) предел функции f в точке 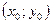 не существует или существует, но не равен ее значению в этой точке.
не существует или существует, но не равен ее значению в этой точке.
Функция f нескольких переменных называется непрерывной на множестве MÌD (f), если она непрерывна в каждой точке этого множества.
Функция f (x; y), определенная в окрестности точки 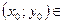 R 2, называется непрерывной в этой точке по переменной x (по переменной y), если существует конечный предел
R 2, называется непрерывной в этой точке по переменной x (по переменной y), если существует конечный предел 
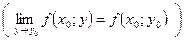 .
.
Очевидно, что непрерывная в точке по совокупности аргументов функция будет непрерывна в этой точке и по каждому аргументу в отдельности. Обратное, вообще говоря, неверно.
Функция 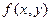 называется равномерно непрерывной на множестве MÌD (f), если
называется равномерно непрерывной на множестве MÌD (f), если
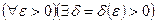
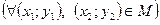
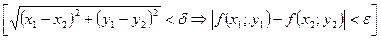
Теорема Кантора. Функция  , непрерывная на ограниченном замкнутом множестве, равномерно непрерывна на этом множестве.
, непрерывная на ограниченном замкнутом множестве, равномерно непрерывна на этом множестве.
Теорема 1 (аналог первой теоремы Вейерштрасса). Действительная функция  , определенная и непрерывная на замкнутом и ограниченном множестве M, ограничена на этом множестве.
, определенная и непрерывная на замкнутом и ограниченном множестве M, ограничена на этом множестве.
Теорема 2 (аналог второй теоремы Вейерштрасса).Действительная функция  , определенная и непрерывная на замкнутом и ограниченном множестве M, принимает на нем свои наименьшее и наибольшее значения.
, определенная и непрерывная на замкнутом и ограниченном множестве M, принимает на нем свои наименьшее и наибольшее значения.
Теорема 3. Если функция f непрерывна в точке M 0(x 0, y 0), не являющейся изолированной точкой D (f), то существует такая окрестность точки M 0, во всех точках которой функция f принимает значения того же знака, что и в точке M 0.
Теорема 4. Если функция f непрерывна на связном множестве X и в точках M 1 Î X и M 2 Î X принимает неравные между собой значения f (M 1) ¹ f (M 2), то она принимает все промежуточные значения между f (M 1) и f (M 2).
Пример 1. Исследовать на непрерывность функцию
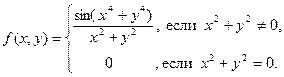
Решение. Имеем D (f) = R 2. В любой точке (x 0, y 0) ¹ (0, 0) данная функция непрерывна по теоремам о непрерывности частного и композиции функций. Подозрительной на разрыв является точка (0; 0). Найдем


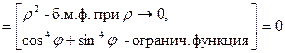 .
.
Т.к. 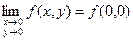 , то функция f (x, y) непрерывна в точке (0, 0).
, то функция f (x, y) непрерывна в точке (0, 0).
|
|
|
|
|
Дата добавления: 2015-04-24; Просмотров: 645; Нарушение авторских прав?; Мы поможем в написании вашей работы!