Обчислення інтегралів Мора способом Верещагіна

Обчислення інтегралів Мора істотно спрощується, якщо одна з епюр (у дійсному чи одиничному стані) прямолінійна при сталому по довжині поперечному перерізі. Ця умова виконується для систем, що складаються з прямих стержнів, оскільки при цьому епю­ри внутрішніх сил від одиничного навантаження (зосередженої сили або пари) завжди обмежені прямими лініями.

Графоаналітичний спосіб визначення інтеграла Мора був запропонований О. М. Верещагіним і має назву способу Верещагіна. Згідно з цим методом загальна формула (2.9) для визначення переміщень у системах з прямих стержнів набирає вигляду

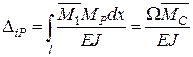, (2.17)

де Ω – площа епюри М_P,

с – її центр ваги,

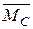–ордината епюри від одиничного навантаження під центром ваги епюри М_Р.

Інтеграл Мора дорівнює добутку площі епюри від зовнішнього навантаження на ординату прямолінійної епюри від одиничного наван­таження, розміщену під центром ваги епюри від заданого зовнішнього навантаження. Обчислення за цією формулою виконують по ділянках, на кожній з яких епюра від одиничного навантаження має бути прямолінійною (рис. 2.12). Тоді, коли обидві епюри прямолінійні, можна множити площу будь-якої з них на ординату іншої під центром ваги першої.

Якщо епюра М_P має складний вигляд, то її слід розбити на прості фігу­ри (рис. 2.13), для яких легко визначити площу і положення центра ваги.

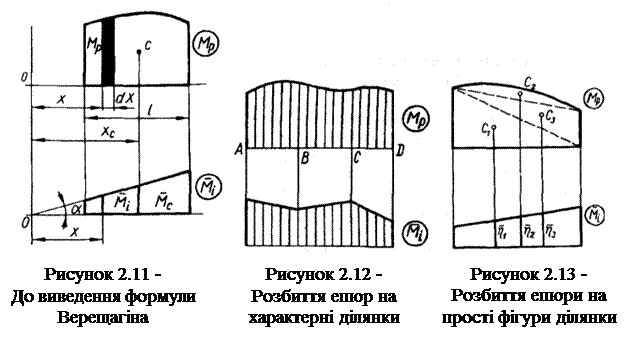
При цьому кожну з площ треба множити на ординату одиничної епюри під центром ваги відповідної площі. Ординати в цьому разі зручно
позначати замість літерами η_k, де k = 1; 2; ….

Отже,

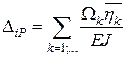. (2.18)

Переміщення від дії осьових і поперечних сил, а також крутних мо­ментів виражаються аналогічно:

; ; ,

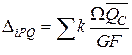де Ω — площа епюри N_Р,або Q_P, або М_Ркр від заданого навантаження;

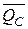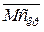, , – ординати відповідних епюр осьових, поперечних сил і крутних моментів від одиничного навантаження, взяті під центрами ваги епюр N_Р, Q_P, М_Ркр.

Якщо епюри від заданого і одиничного навантажень протилежні за знаком, то їхній добуток має знак «мінус».

Спосіб Верещагіна широко застосовують при розрахунку рамних конст­рукцій (конструкцій, в яких кути в місцях з'єднання окремих стержнів, жорсткі до деформації, залишаються жорсткими після неї).

Розглянемо приклади застосування способу Верещагіна для визначення переміщень у стержневих системах.

Визначимо прогин у точці D і кут повороту перерізу В консолі (рис. 2.14, а). Відповідні допоміжні (одиничні) стани зображено на рис. 2.14, б, в.

Будуємо епюри згинальних моментів М_Р і .Прогин у точці D бал­ки за Верещагіним

.

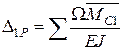На ділянці АВ площа епюри .Центр ваги цієї площі, обмеженої квадратич­ною параболою 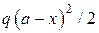(рис. 2.14, а), роз­міщений на відстані (3/4)а від точки В. Ордината допоміжної епюри 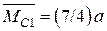. На ділянці BD Ω = 0. Отже,

.

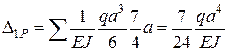Для визначення кута повороту допоміжну систему навантажимо одиничною парою. Оче­видно, 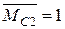. Отже, кут повороту перерізу В

.

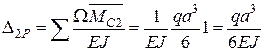Для визначення переміщень використовують також і інші способи, які ґрунтуються на способі Верещагіна - спосіб Верещагіна-Даркова та Сімпсона-Карнаухова (додаток Ж).

Дата добавления: 2015-03-29