
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Заготовки и последующей ковки
|
|
|
|
Пространственные погрешности поковок за счет дефекта резки исходной
Качество торцовой поверхности поковок после ковки
И радиально-ковочных машинах
Пространственные погрешности поковок после ковки на вертикальных
И радиально-ковочных машинах
Качество наружной поверхности поковок, полученных на вертикальных
| r: R | А при n | |||
| 0,4 | 0,0018 | 0,0018 | 0,0034 | 0,0068 |
| 0,5 | 0,0011 | 0,0020 | 0,0036 | 0,0071 |
| 0,6 | 0,0010 | 0,0019 | 0,0035 | 0,0068 |
| 0,7 | 0,0008 | 0,0016 | 0,0031 | 0,0060 |
| 0,8 | 0,0006 | 0,0012 | 0,0023 | 0,0045 |
| 0,9 | 0,0004 | 0,0008 | 0,0012 | 0,0023 |
| Высота микрогеометрической погрешности (огранка) h = AR мм, где R – радиус бойка в мм; A – коэффициент, зависящий от отношения радиуса поковки r к радиусу бойка R и числа оборотов n поковки в процессе ковки. Примечания: 1. Величину обезуглероженного слоя следует определять из соотношения Т =0,01 d мм, где d — номинальный диаметр детали по чертежу в мм 2. При повышенных требования к точности и чистоте поверхности к расчетному припуску прибавлять 0,2. | ||||
| Таблица 12 |
| Диаметр поковки, мм | Удельная кривизна Δ 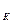 , мкм на 1 мм длины проката , мкм на 1 мм длины проката
|
| До 60 | |
| Св.60 | |
| Определение суммарных значений погрешности ρ, см табл. 6. Таблица 13 |
| Диаметр торцовой поверхности D, мм | R 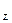 , мкм , мкм
| Т, мкм |
| До 30 | ||
| 30...50 | ||
| 50...80 | ||
| 80...120 |
Таблица 14
| Диаметр торцовой поверхности D, мм | Величина дефекта ρ, мм |
| До 30 | 1,5 |
| 30...50 | 2,5 |
| 50...80 | |
| 80...120 | |
Примечания:
1. Для промежуточных торцовых поверхностей пространственной погрешностью является погрешность торца, определяемая по формуле: r1 = ΔH 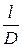 , где ΔH — удельная величина неперпендикулярности принимают для диаметра торцовой поверхности до 60 мм, равной 0,05 мкм/мм и для диаметра свыше 60 мм — 0,1 мкм/мм; l — расстояние в мм от середины наибольшего диаметра ступеней по торцовой поверхности, пространственную погрешность которой определяют; D – диаметр торцовой поверхности в мм
2. Для поверхности концевых ступеней пространственную погрешность определяют по формуле: , где ΔH — удельная величина неперпендикулярности принимают для диаметра торцовой поверхности до 60 мм, равной 0,05 мкм/мм и для диаметра свыше 60 мм — 0,1 мкм/мм; l — расстояние в мм от середины наибольшего диаметра ступеней по торцовой поверхности, пространственную погрешность которой определяют; D – диаметр торцовой поверхности в мм
2. Для поверхности концевых ступеней пространственную погрешность определяют по формуле: 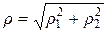 , где r1 — погрешность за счет неперпендикулярности торца; r2 — погрешность за счет дефектов резки. , где r1 — погрешность за счет неперпендикулярности торца; r2 — погрешность за счет дефектов резки.
|
Таблица 15
|
|
|
|
|
Дата добавления: 2015-04-24; Просмотров: 372; Нарушение авторских прав?; Мы поможем в написании вашей работы!