
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Теоремы о равносильности уравнений
|
|
|
|
Вывод
При решении уравнений необходимо следить за изменением множества допустимых значений неизвестного. В случае расширения его следует проверять, не является ли найденное решение посторонним для данного уравнения. В случае сужения необходимо убедиться, не являются ли выпавшие значения неизвестных решениями данного уравнения. Задача нахождения потерянных решений не всегда легко выполнима, поэтому желательно избегать тождественных преобразований, ведущих к сужению множества допустимых значений неизвестных уравнения.
Примеры. Равносильны ли уравнения в поле действительных чисел?
9. 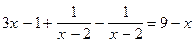 (1) и
(1) и 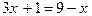 (2)
(2)
Решение
Область допустимых значений первого уравнения:
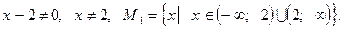
Область допустимых значений второго уравнения - множество всех действительных чисел: 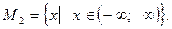
Произошло расширение области допустимых значений первого уравнения, поэтому возможно появление посторонних корней.
Первое уравнение не имеет корней, так как 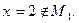
Второе уравнение имеет корень: 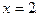
При расширении области допустимых значений появился посторонний корень 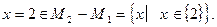
Уравнения не будут равносильными.
Ответ: не равносильны.
10. 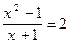 (1) и
(1) и 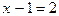 (2)
(2)
Решение
Область допустимых значений первого уравнения:
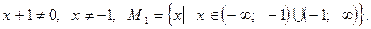
Область допустимых значений второго уравнения - множество всех действительных чисел: 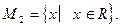
Область допустимых значений уравнения (1) расширилась, значит возможно появление посторонних корней. Проверим это.
Первое уравнение имеет корень: 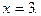
Второе уравнение имеет корень: 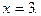
Посторонние корни не появились - уравнения равносильны.
Ответ: равносильны.
11. 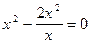 (1) и
(1) и 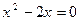 (2).
(2).
Решение
Область допустимых значений первого уравнения:
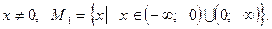
Область допустимых значений второго уравнения - множество всех действительных чисел: 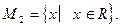
Область допустимых значений уравнения (1) расширилась - возможно появление посторонних корней.
Первое уравнение имеет один корень: 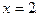
Второе уравнение имеет два корня: 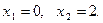
Появился посторонний корень: 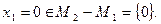
Ответ: не равносильны.
12. 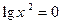 (1) и
(1) и 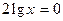 (2).
(2).
Решение
Область допустимых значений первого уравнения:
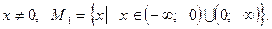
Область допустимых значений второго уравнения:
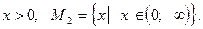
Область допустимых значений первого уравнения сузилась, возможна потеря корней. Проверим это.
Первое уравнение имеет два корня: 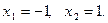
Второе уравнение имеет один корень: 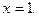
Произошла потеря корня 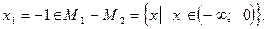
Уравнения не равносильны.
Ответ: не равносильны.
13. 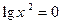 (1) и
(1) и  (2).
(2).
Решение
Область допустимых значений первого уравнения:
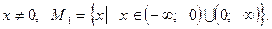
Область допустимых значений второго уравнения:
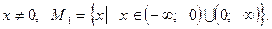
Области допустимых значений равны: 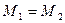 , значит уравнения равносильны. В самом деле, первое уравнение имеет два корня:
, значит уравнения равносильны. В самом деле, первое уравнение имеет два корня: 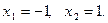
Второе уравнение имеет корни: 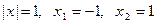
Ответ: равносильны.
14. 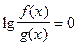 (1) и
(1) и 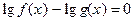 (2).
(2).
Решение
Область допустимых значений первого уравнения находится как решение совокупности двух систем неравенств: 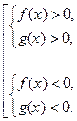
Область допустимых значений второго уравнения находится из одной системы неравенств: 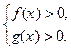
Область допустимых значений сузилась, а поэтому возможна потеря корней, значит уравнения могут быть не равносильны.
Ответ: могут быть не равносильны.
15. 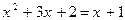 (1) и
(1) и 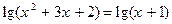 (2)
(2)
Решение
Область допустимых значений первого уравнения - множество всех действительных чисел: 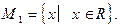
Область допустимых значений второго уравнения найдем из решения системы неравенств (см. рис. 3):
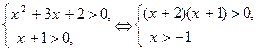
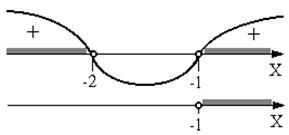
Рис. 3
Получим множество: 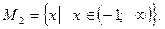
Область допустимых значений сузилась, поэтому возможна потеря корней.
Первое уравнение имеет один корень: 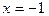
Второе уравнение не имеет корней. Значит, уравнения не равносильны.
Ответ: не равносильны.
16. 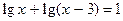 (1) и
(1) и 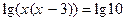 (2)
(2)
Решение
Область допустимых значений первого уравнения найдем из решения системы неравенств: 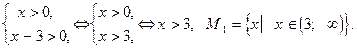
Область допустимых значений второго уравнения найдем из решения неравенства 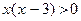 методом промежутков (см. рис. 4).
методом промежутков (см. рис. 4).
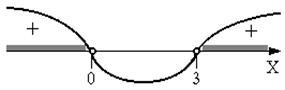
Рис. 4
Получим множество: 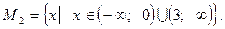
Область допустимых значений уравнения (1) расширилась, поэтому возможно появление посторонних корней. Проверим это.
Первое уравнение имеет один корень: 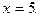
Второе уравнение имеет два корня: 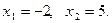
Появился посторонний корень 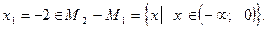
Значит, уравнения не равносильны.
Ответ: не равносильны.
Задание 1
Равносильны ли уравнения в поле действительных чисел?
1. 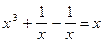 (1) и
(1) и 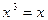 (2). 2.
(2). 2. 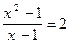 (1) и
(1) и 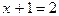 (2).
(2).
3.  (1) и
(1) и 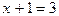 (2). 4.
(2). 4. 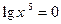 (1) и
(1) и  (2).
(2).
5. 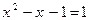 (1) и
(1) и 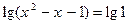 (2).
(2).
6. 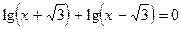 (1) и
(1) и 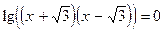 (2).
(2).
7. 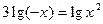 (1) и
(1) и 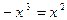 (2).
(2).
При решении уравнений выполняются преобразования, основанный на теоремах о равносильности уравнений.
Теорема 1. Уравнения
 =
= 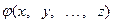 (1)
(1)
и
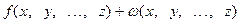 =
= 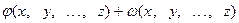 (2)
(2)
равносильны, если функция 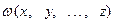 определена на множестве всех допустимых значений неизвестных уравнения (1).
определена на множестве всех допустимых значений неизвестных уравнения (1).
Замечание. Если 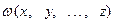 определена не при всех допустимых значениях неизвестных уравнения (1) и теряет смысл при каких-либо системах значений неизвестных, являющихся решением уравнения (1), то при переходе от уравнения (1) к уравнению (2) произойдет потеря корней.
определена не при всех допустимых значениях неизвестных уравнения (1) и теряет смысл при каких-либо системах значений неизвестных, являющихся решением уравнения (1), то при переходе от уравнения (1) к уравнению (2) произойдет потеря корней.
Примеры: 1) Дано уравнение 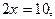 которое имеет только один корень
которое имеет только один корень 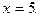
а) прибавим к обеим частям уравнения функцию 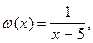 теряющую смысл при
теряющую смысл при 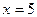 . Получим уравнение
. Получим уравнение 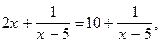 не равносильное данному, так как
не равносильное данному, так как 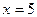 не является его корнем.
не является его корнем.
б) Прибавим к обеим частям уравнения функцию 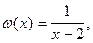 теряющую смысл при
теряющую смысл при 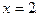
Получим уравнение  равносильное данному, так как оно тоже имеет только один корень
равносильное данному, так как оно тоже имеет только один корень 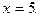
2) Дано уравнение  областью допустимых значений неизвестного является множество всех действительных чисел
областью допустимых значений неизвестного является множество всех действительных чисел 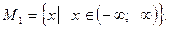 .
.
Уравнение имеет два корня: 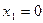 и
и 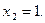
Прибавим к обеим частям данного уравнения функцию 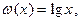 область определения которой
область определения которой 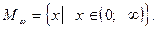
Получим уравнение 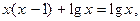 не равносильное данному, так как
не равносильное данному, так как 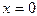 не является его корнем.
не является его корнем.
Теорема 2. Уравнения
 =
= 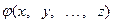 (1)
(1)
и
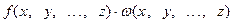 =
= 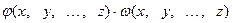 (2)
(2)
равносильны, если функция 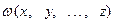 определена и отлична от нуля на множестве всех допустимых значений неизвестных уравнения (1).
определена и отлична от нуля на множестве всех допустимых значений неизвестных уравнения (1).
Замечание. Если условия теоремы, касающиеся функции 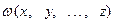 , не выполняются, то уравнение (2) может быть не равносильно уравнению (1). Может произойти потеря решений, если
, не выполняются, то уравнение (2) может быть не равносильно уравнению (1). Может произойти потеря решений, если 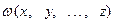 теряет смысл при каких-либо системах значений неизвестных, являющихся решениями уравнения (1).
теряет смысл при каких-либо системах значений неизвестных, являющихся решениями уравнения (1).
Уравнение (2) может иметь посторонние решения для уравнения (1), если 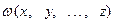 при некоторых допустимых системах значений неизвестных равна нулю, но эта система значений неизвестных не является решением уравнения (1).
при некоторых допустимых системах значений неизвестных равна нулю, но эта система значений неизвестных не является решением уравнения (1).
Примеры. Дано уравнение 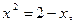 множеством допустимых значений x является множество всех действительных чисел
множеством допустимых значений x является множество всех действительных чисел 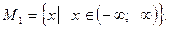 Уравнение имеет два корня:
Уравнение имеет два корня: 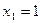 и
и 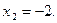
а) Умножим обе части данного уравнения на 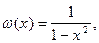 теряющую смысл при
теряющую смысл при  и
и 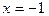 Получим уравнение
Получим уравнение  не равносильное данному, так как оно имеет только один корень
не равносильное данному, так как оно имеет только один корень 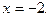 Умножение обеих частей данного уравнения на
Умножение обеих частей данного уравнения на 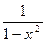 привело к потере корня
привело к потере корня  .
.
б) Умножим обе части данного уравнения на  теряющую смысл при
теряющую смысл при 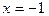 Получим уравнение
Получим уравнение 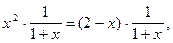 равносильное данному, так как оно имеет два корня:
равносильное данному, так как оно имеет два корня: 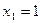 и
и 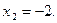
в) Умножим обе части данного уравнения на 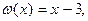 обращающуюся в нуль при
обращающуюся в нуль при 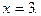 Получим уравнение
Получим уравнение 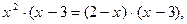 не равносильное данному, так как оно имеет три корня:
не равносильное данному, так как оно имеет три корня: 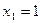 ,
, 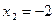 и
и 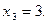
Умножение обеих частей данного уравнения на 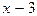 привело к появлению постороннего корня
привело к появлению постороннего корня 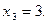
Равносильны ли уравнения на множестве действительных чисел?
Пример 1. 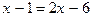 (1) и
(1) и 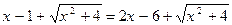 (2).
(2).
Решение
Областью допустимых значений первого уравнения является множество всех действительных чисел 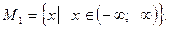 Оно имеет один корень
Оно имеет один корень 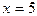 .
.
К обеим частям этого уравнения прибавляется функция 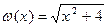 , которая определена также при всех действительных значениях x, значит она не изменяет область определения уравнения (1), а поэтому получается уравнение (2) равносильное уравнению (1), имеющее также один корень
, которая определена также при всех действительных значениях x, значит она не изменяет область определения уравнения (1), а поэтому получается уравнение (2) равносильное уравнению (1), имеющее также один корень 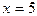 . Уравнения равносильны.
. Уравнения равносильны.
Ответ: равносильны.
Пример 2. 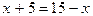 (1) и
(1) и 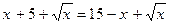 (2).
(2).
Решение
Областью допустимых значений первого уравнения является множество всех действительных чисел 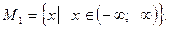 Оно имеет один корень
Оно имеет один корень 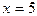 .
.
К обеим частям уравнения (1) прибавляется функция 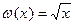 , областью определения которой является множество
, областью определения которой является множество 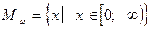 , в которое входит корень первого уравнения. Поэтому, несмотря на сужение области допустимых значений уравнения (1), получается равносильное уравнение, имеющее также один корень
, в которое входит корень первого уравнения. Поэтому, несмотря на сужение области допустимых значений уравнения (1), получается равносильное уравнение, имеющее также один корень 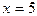 .
.
Ответ: равносильны.
Пример 3. 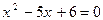 (1) и
(1) и 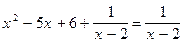 . (2)
. (2)
Решение
Областью допустимых значений первого уравнения является множество всех действительных чисел 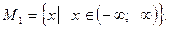 Оно имеет два корня:
Оно имеет два корня: 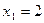 и
и 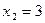 . К его обеим частям прибавляется функция
. К его обеим частям прибавляется функция 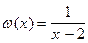 , которая имеет область определения
, которая имеет область определения 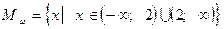 и теряет смысл при
и теряет смысл при 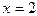 , который является корнем первого уравнения, а поэтому второе уравнение имеет только один корень
, который является корнем первого уравнения, а поэтому второе уравнение имеет только один корень 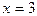 , а значит уравнения не равносильны.
, а значит уравнения не равносильны.
Ответ: не равносильны.
Пример 4. 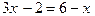 (1) и
(1) и 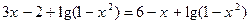 . (2)
. (2)
Решение
Областью допустимых значений первого уравнения является множество всех действительных чисел 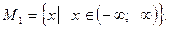 Оно имеет один корень:
Оно имеет один корень: 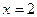 .
.
К обеим частям уравнения прибавляется функция 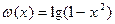 , которая определена на множестве:
, которая определена на множестве:
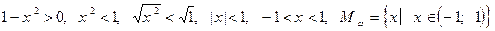 .
.
Область допустимых значений первого уравнения сузилась настолько, что корень первого уравнения не входит в это множество и не является корнем второго уравнения, значит уравнения не равносильны.
Ответ: не равносильны.
Пример 5. 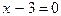 (1) и
(1) и 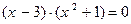 . (2)
. (2)
Решение
Областью допустимых значений первого уравнения является множество всех действительных чисел 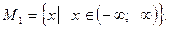 Оно имеет один корень:
Оно имеет один корень: 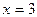 .
.
Обе части уравнения умножаются на функцию  , которая также определена на множестве всех действительных чисел
, которая также определена на множестве всех действительных чисел 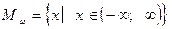 и при
и при 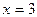 не обращается в нуль, значит получим уравнение (2) равносильное уравнению (1).
не обращается в нуль, значит получим уравнение (2) равносильное уравнению (1).
Ответ: равносильны.
Пример 6. 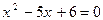 (1) и
(1) и 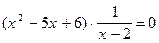 . (2)
. (2)
Решение
Областью допустимых значений первого уравнения является множество всех действительных чисел 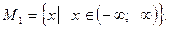 Оно имеет два корня:
Оно имеет два корня: 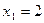 и
и 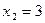 . Обе части уравнения умножаются на функцию
. Обе части уравнения умножаются на функцию 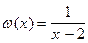 , которая имеет область определения
, которая имеет область определения 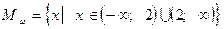 и, несмотря на то, что не обращается в нуль при
и, несмотря на то, что не обращается в нуль при 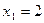 и
и 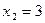 , но теряет смысл при
, но теряет смысл при 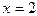 , а поэтому второе уравнение имеет только один корень
, а поэтому второе уравнение имеет только один корень 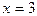 , а значит уравнения не равносильны.
, а значит уравнения не равносильны.
Ответ: не равносильны.
Пример 7.  (1) и
(1) и 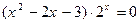 . (2)
. (2)
Решение
Областью допустимых значений первого уравнения является множество всех действительных чисел 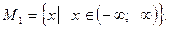 Оно имеет два корня:
Оно имеет два корня: 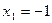 и
и 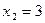 . Обе части уравнения умножаются на показательную функцию
. Обе части уравнения умножаются на показательную функцию  , которая имеет область определения - множество всех действительных чисел
, которая имеет область определения - множество всех действительных чисел 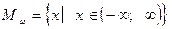 и, более того, она положительна при всех x из области определения и ни при каких значениях x не равна нулю, поэтому второе уравнение также имеет два корня
и, более того, она положительна при всех x из области определения и ни при каких значениях x не равна нулю, поэтому второе уравнение также имеет два корня 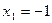 и
и 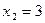 , а значит уравнения равносильны.
, а значит уравнения равносильны.
Ответ: равносильны.
Решение этого примера можно распространить на более общий случай:
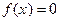 (1) и
(1) и 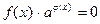 (2)
(2)
Функция 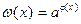 положительна при всех x из области определения функции
положительна при всех x из области определения функции 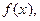 если к тому же функция
если к тому же функция 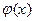 определена при значениях корней уравнения (1), тогда уравнения (1) и (2) равносильны. Если функция
определена при значениях корней уравнения (1), тогда уравнения (1) и (2) равносильны. Если функция 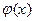 не определена при значении хотя бы одного из корней уравнения (1), тогда уравнения (1) и (2) не равносильны.
не определена при значении хотя бы одного из корней уравнения (1), тогда уравнения (1) и (2) не равносильны.
Пример 8. 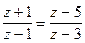 (1) и
(1) и 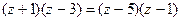 . (2)
. (2)
Решение
Областью допустимых значений первого уравнения является множество:
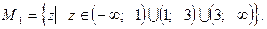
Оно имеет один корень 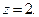
Обе части первого уравнения умножаются на функцию 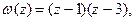 которая определена при всех значениях z из множества действительных чисел
которая определена при всех значениях z из множества действительных чисел 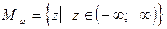 и не обращается в нуль при
и не обращается в нуль при 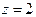 , которое является корнем уравнения (1), поэтому уравнение (2) имеет один корень
, которое является корнем уравнения (1), поэтому уравнение (2) имеет один корень 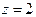 . Уравнения (1) и (2) равносильны.
. Уравнения (1) и (2) равносильны.
Ответ: равносильны.
Пример 9. 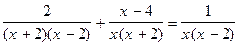 (1) и
(1) и 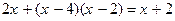 . (2)
. (2)
Решение
Областью допустимых значений первого уравнения является множество:
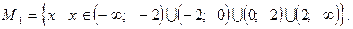
Оно имеет один корень: 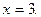
Обе части первого уравнения умножаются на функцию 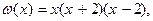 которая определена при всех значениях x из множества действительных чисел
которая определена при всех значениях x из множества действительных чисел 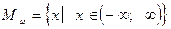 , и не обращается в нуль при
, и не обращается в нуль при 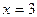 , которое является корнем уравнения (1). Но в результате такого умножения произошло расширение области допустимых значений уравнения (1) и возможно появление посторонних корней. Проверим это. Уравнение (2) имеет два корня
, которое является корнем уравнения (1). Но в результате такого умножения произошло расширение области допустимых значений уравнения (1) и возможно появление посторонних корней. Проверим это. Уравнение (2) имеет два корня 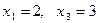 . Поэтому уравнения (1) и (2) не равносильны.
. Поэтому уравнения (1) и (2) не равносильны.
Ответ: не равносильны.
Пример 10. 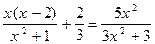 (1) и
(1) и  . (2)
. (2)
Решение
Областью допустимых значений первого уравнения является множество всех действительных чисел 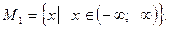 Оно имеет один корень:
Оно имеет один корень: 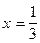 .
.
Обе части первого уравнения умножаются на функцию 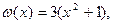 которая определена при всех значениях x из множества действительных чисел
которая определена при всех значениях x из множества действительных чисел 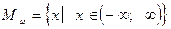 , и не обращается в нуль при
, и не обращается в нуль при 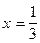 , которое является корнем уравнения (1). Значит область допустимых значений уравнения (1) не изменилась. Остается проверить корни уравнения (2) - оно имеет один корень -
, которое является корнем уравнения (1). Значит область допустимых значений уравнения (1) не изменилась. Остается проверить корни уравнения (2) - оно имеет один корень - 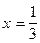 , значит уравнения равносильны.
, значит уравнения равносильны.
Ответ: равносильны.
Пример 11. 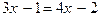 (1) и
(1) и 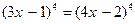 . (2)
. (2)
Решение
Областью допустимых значений первого уравнения является множество всех действительных чисел 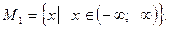 Оно имеет один корень:
Оно имеет один корень: 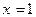 .
.
Уравнение (2) получается возведением обеих частей уравнения (1) в четную - 4-й степень. Область допустимых значений не изменилась, уравнение (2) определено на множестве всех действительных чисел: 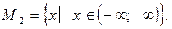
Посмотрим какие корни оно имеет? Для этого надо из обеих частей уравнения (2) извлечь корень 4-й степени, тогда получим:
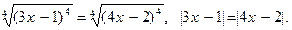
Чтобы решить последнее уравнение, установим точки, при которых каждое из выражений под модулем обращается в нуль, получим три промежутка, на каждом из которых решим уравнение (см. рис. 5):
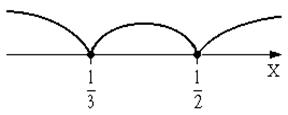
Рис. 5
При 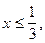 получим уравнение
получим уравнение 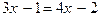 ,
, 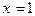 . Но
. Но 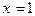 не входит в промежуток
не входит в промежуток 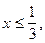 значит не является корнем уравнения.
значит не является корнем уравнения.
При 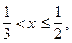 получим уравнение
получим уравнение 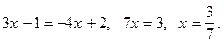
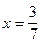 входит в промежуток
входит в промежуток 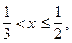 значит является корнем уравнения.
значит является корнем уравнения.
При 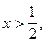 получим уравнение
получим уравнение 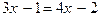 ,
, 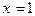 .
. 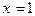 входит в промежуток
входит в промежуток 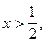 значит является корнем уравнения.
значит является корнем уравнения.
Таким образом, уравнение (2) имеет два корня 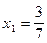 и
и 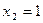 .
.
Следовательно, при возведении обеих частей уравнения в четную степень возможно появление посторонних корней.
Ответ: уравнения не равносильны.
Пример 12. 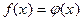 (1) и
(1) и 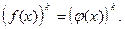 (2)
(2)
Решение
Если k - нечетное число, тогда уравнения равносильны, если k - четное число, то, вообще говоря, не равносильны, ибо второе уравнение примет вид:
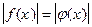 или
или 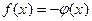 и
и 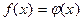 , т. е. распадается на два уравнения. Только в том случае, если уравнение
, т. е. распадается на два уравнения. Только в том случае, если уравнение 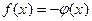 , по каким-то причинам не будет иметь корней, мы можем получить равносильные уравнения.
, по каким-то причинам не будет иметь корней, мы можем получить равносильные уравнения.
Ответ: при k нечетном - равносильны, при k четном - не равносильны.
Пример 13. 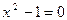 (1) и
(1) и 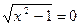 . (2)
. (2)
Решение
Областью допустимых значений первого уравнения является множество всех действительных чисел 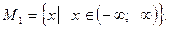 Оно имеет два корня:
Оно имеет два корня: 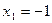
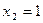 .
.
Второе уравнение получается из первого извлечением квадратного корня из обеих частей первого уравнения. В результате область допустимых значений сузилась и стала: 
Однако, корни уравнения остались теми же, второе уравнение имеет тоже два корня: 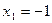
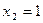 и потому, уравнения равносильны.
и потому, уравнения равносильны.
Ответ: равносильны.
Пример 14.  (1) и
(1) и 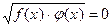 . (2)
. (2)
Решение
Область допустимых значений первого уравнения определяется системой неравенств: 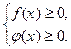
Область допустимых значений второго уравнения определяется совокупностью систем неравенств: 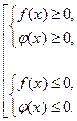
Уравнения могут быть равносильны, если выполняется система неравенств:
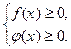
Ответ: равносильны, если 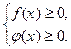
Пример 15. При каком условии уравнения
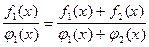 (1) и
(1) и 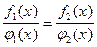 (2)
(2)
равносильны?
Решение
Если 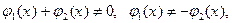 тогда уравнения будут иметь одинаковые области допустимых значений и будут равносильны.
тогда уравнения будут иметь одинаковые области допустимых значений и будут равносильны.
Ответ: если 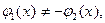 тогда уравнения равносильны.
тогда уравнения равносильны.
Пример 16. Будут ли равносильны уравнения на множестве действительных чисел
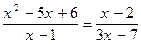 (1) и
(1) и 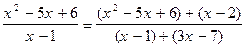 (2)?
(2)?
Решение
Область допустимых первого уравнения - множество:
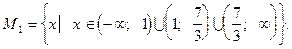
Оно имеет два корня: 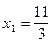 и
и 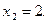
Область допустимых значений второго уравнения находим из решения системы неравенств: 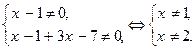
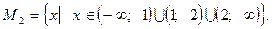
Область допустимых значений изменилась, поэтому возможна как потеря корней, так и появление посторонних корней.
Найдем решения уравнения (2). Оно имеет только один корень: 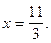
Уравнения не равносильны.
Ответ: не равносильны.
Задание 2
Равносильны ли уравнения на множестве действительных чисел?
1. 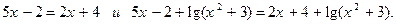
2. 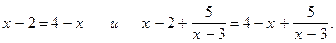
3. 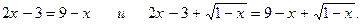

4. 
5. 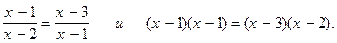
6. 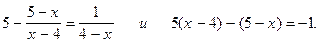
7. 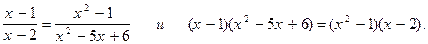
8. 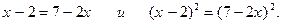
9. 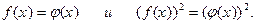
10. Будут ли равносильны уравнения на множестве действительных чисел?
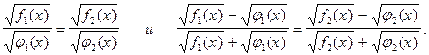
11. Верно ли утверждение, что уравнения
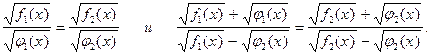
равносильны на множестве действительных чисел?
12. Будут ли равносильны уравнения на множестве действительных чисел?
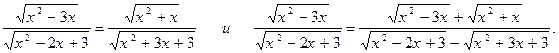
Выводы
|
|
|
|
|
Дата добавления: 2015-04-24; Просмотров: 1219; Нарушение авторских прав?; Мы поможем в написании вашей работы!