Потеря корней возможна в следующих случаях

Появление посторонних корней возможно в следующих случаях

1. При умножении обеих частей уравнения на функцию, если эта функция при некоторых допустимых значениях неизвестных равна нулю, но эти значения не являются корнями исходного уравнения. (При освобождении от знаменателя, содержащего неизвестную величину.)

2. При тождественных преобразованиях, расширяющих область допустимых значений исходного уравнения:

возведении обеих частей уравнения в четную степень:

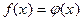и 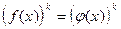, где k - четное;

применение свойства корней - переход от 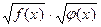к ;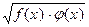

применении свойства логарифмов: 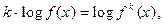если k - четное;

применении свойства логарифмов:

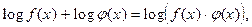
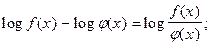
переходе от логарифмических уравнений к алгебраическим:

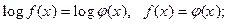
логарифмирование уравнения, у которого содержит показательные функции:

например,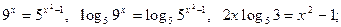

возможны и другие случаи.

1. Если к обеим частям уравнения прибавляется функция, определенная при всех допустимых значениях неизвестных заданного уравнения, но теряющая смысл при каких-либо значениях неизвестных, являющихся решением данного уравнения.

2. Если обе части уравнения умножаются на функцию, определенную и не равную нулю при всех допустимых значениях неизвестных, но теряющую смысл при каких-либо значениях неизвестных, являющихся решениями данного уравнения.

3. При тождественных преобразованиях, сужающих область допустимых значений неизвестных уравнения:

извлечение корня четной степени из обеих частей уравнения

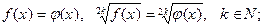
извлечение корней четной степени из произведения

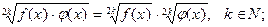
преобразование логарифма произведения или частного в сумму или разность логарифмов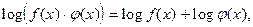

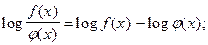
применении свойства логарифмов: 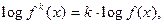если k - четное;

логарифмирование обеих частей уравнения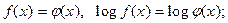

возможны и другие случаи.

1.5. Приемы решения уравнений, позволяющие отбрасывать посторонние корни и избежать потери корней*

Дата добавления: 2015-04-24