
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Й способ
|
|
|
|
Й способ
Область допустимых значений: 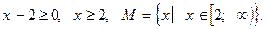
Тогда, уравнение равносильно совокупности двух смешанных систем:
(1) 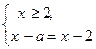 и (2)
и (2) 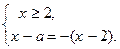
Решим каждую систему:
(1) 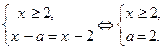 Это значит, что при
Это значит, что при 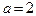 уравнение имеет бесконечное множество решений из промежутка
уравнение имеет бесконечное множество решений из промежутка 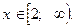
(2) 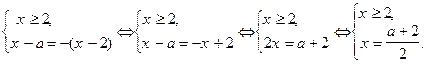
Чтобы найти значения параметра a, при которых уравнение будет иметь решение 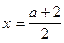 подставим вместо x в неравенство системы, значение
подставим вместо x в неравенство системы, значение 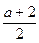 и решим полученное неравенство относительно a.
и решим полученное неравенство относительно a.
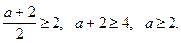
Но поскольку, мы установили, что при a = 2 уравнение имеет множество решений их промежутка 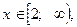 тогда при
тогда при  уравнение будет иметь решение
уравнение будет иметь решение 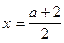 .
.
Осталось выяснить решения уравнения при 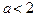 .
.
Из первой системы находим:
(1) 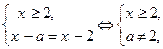 уравнение не имеет решений.
уравнение не имеет решений.
Из второй системы мы нашли решения при  , в противном случае, т. е. при
, в противном случае, т. е. при 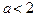 уравнение не будет иметь решений.
уравнение не будет иметь решений.
Область допустимых значений: 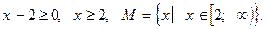
Воспользуемся свойством абсолютной величины: 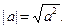
Получим уравнение: 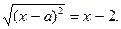 Возведем обе части этого уравнения в квадрат, получим:
Возведем обе части этого уравнения в квадрат, получим:
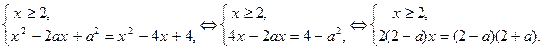
1. Если a = 2, тогда уравнение примет вид: 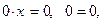 уравнение имеет бесконечное множество решений из промежутка
уравнение имеет бесконечное множество решений из промежутка 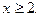
2. Если 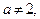 тогда уравнение имеет решение
тогда уравнение имеет решение 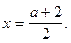 Чтобы выяснить значения a, надо решить неравенство
Чтобы выяснить значения a, надо решить неравенство 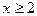 , куда вместо x подставить значение
, куда вместо x подставить значение 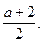
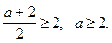 Учитывая, что при a = 2
Учитывая, что при a = 2 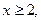 получаем:
получаем: 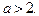
Таким образом, при 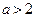 уравнение имеет решение
уравнение имеет решение 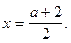
3. При 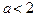 , очевидно, уравнение не имеет решений.
, очевидно, уравнение не имеет решений.
Ответ:
1. Если a = 2, тогда уравнение имеет бесконечное множество решений из промежутка 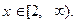
2. Если a > 2, тогда уравнение имеет единственное решение 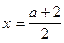 .
.
3. Если 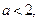 то уравнение не имеет решений.
то уравнение не имеет решений.
б) 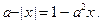
Решение
Если 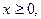 тогда будем иметь уравнение:
тогда будем иметь уравнение: 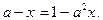
После простых преобразований получим (a - 1)(a + 1)x = 1 - a.
При 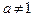 и
и 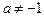 уравнение имеет единственное решение
уравнение имеет единственное решение 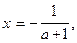 но учитывая, что
но учитывая, что 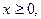 находим,
находим, 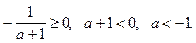
Отсюда ясно, что при 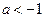 уравнение имеет единственное решение
уравнение имеет единственное решение
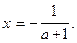
При a = -1 получаем уравнение 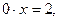 которое не имеет решений.
которое не имеет решений.
При a = 1 уравнение примет вид 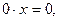 которое имеет бесконечное множество решений на промежутке
которое имеет бесконечное множество решений на промежутке 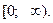
Если x < 0, тогда получим уравнение 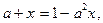 которое преобразуется в уравнение
которое преобразуется в уравнение 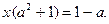 Оно имеет единственное решение
Оно имеет единственное решение 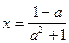 при любых действительных значениях a, но, учитывая, что x должно быть отрицательным, находим для a значения: 1 - a < 0, a > 1.
при любых действительных значениях a, но, учитывая, что x должно быть отрицательным, находим для a значения: 1 - a < 0, a > 1.
Остается выяснить решение уравнения при -1 < a < 1.
Нетрудно установить, что, в этом случае, уравнение не имеет корней.
В самом деле:
1) Если 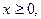 находим:
находим: 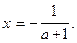
Поскольку 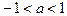 , тогда
, тогда 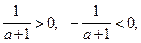 что невозможно, ибо
что невозможно, ибо  значит уравнение не имеет решений.
значит уравнение не имеет решений.
2) Если 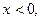 находим:
находим: 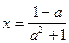 .
.
Поскольку 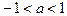 , тогда
, тогда 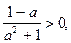 что невозможно, так как
что невозможно, так как 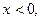 значит уравнение также не имеет решений.
значит уравнение также не имеет решений.
Ответ:
1. Если 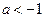 , тогда
, тогда 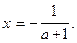
2. Если 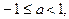 тогда уравнение не имеет решений.
тогда уравнение не имеет решений.
3. Если a = 1, тогда 
4. Если a > 1, тогда 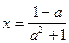 .
.
Пример 8. Решите уравнение |2 - |1 - |x = 1.
Решение
Решать будем это уравнение последовательно " раскрывая " модули, начиная с " внешнего " и " приближаясь " к переменной x.
После раскрытия первого модуля, получим совокупность двух уравнений:
(1) 2 - |1 - |x|| = 1 или (2) 2 - |1 - |x|| = - 1.
Решая уравнение (1), в свою очередь, получаем два уравнения:
|1 - |x|| = 1,
(3) 1 - |x| = 1 или (4) 1 - |x| = -1.
Из уравнения (3) находим: |x| = 0, 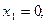 из уравнения (4) находим: |x| = 2,
из уравнения (4) находим: |x| = 2, 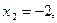

Решая уравнение (2), также получим: |1 - |x|| = 3, которое распадается два уравнения: (3') 1 - |x| = -3 или (4') 1 - |x| = 3.
Из (3') получаем: |x| = 4, 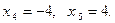 Из (4') |x| = -2, которое не имеет решений.
Из (4') |x| = -2, которое не имеет решений.
Ответ: 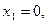
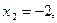
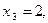
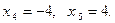
Задание 2
Решите уравнения аналитически и графически.
1. 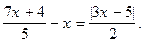 2. |4x - 1| - |2x - 3| + |x - 2| = 0. 3.
2. |4x - 1| - |2x - 3| + |x - 2| = 0. 3. 
Решите уравнения.
4. |x - a| + |x + a + 1| = 3. 5. 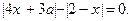
|
|
|
|
|
Дата добавления: 2015-04-24; Просмотров: 449; Нарушение авторских прав?; Мы поможем в написании вашей работы!