Квадратное уравнение с числовыми коэффициентами

Решение и исследование квадратных уравнений

Упражнения

30. Найдите уравнение треугольного импульса на промежутке 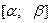с амплитудой (высотой), равной h (см. рис. 22).

Рис. 22

Решите задачу двумя способами: получив непосредственно уравнение соответствующей ломаной с помощью формул (5) и (6) и с помощью преобразований единичного треугольного импульса, уравнение которого было получено.

31. Найдите уравнение вида (1) ломаных, изображенных на рисунке 23:

Рис. 23

32. Постройте графики данных функций, пользуясь описанным "методом вершин":

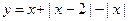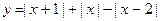а) ; б) ; в) .

33. Изобразите график функции 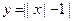, построив для этого сначала график y = |x| - 1, и с его помощью представьте эту функцию в виде (3).

34. Представьте в виде (1) функции, заданные следующими формулами:

1) y = ||x - 2| - 1|; 2) y = x + |x - |x||; 3) y = |x - 2|x|| - |x|; 4) y = x| - 2| - 1|.

Указание. Воспользуйтесь методом, предложенным в задаче 33.

Определение. Уравнение вида где a, b, с - действительные числа, причем 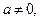x - переменная, называется квадратным.

Дискриминантом квадратного уравнения называется число, составленное из коэффициентов уравнения: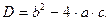

По значению дискриминанта можно установить число решений уравнения или узнать, имеет ли оно решение вообще, т. е. исследовать уравнение.

1-й случай. D > 0. Уравнение имеет два различных действительных корня (действительных, т. е. принадлежащих множеству действительных чисел):

Если построить график квадратной функции 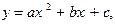то окажется, что он в двух точках пересекает ось OX, которые и являются корнями уравнения. Причем, если a > 0, то ветви графика (параболы) будут направлены вверх, при 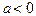- ветви направлены вниз. Это показано на рис. 24 и рис. 25.

Попутно следует заметить, что если a > 0, то трехчлен (y) принимает положительные значения (y > 0) при а отрицательные значения (y < 0) при 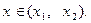Мы заведомо считаем что

Если a < 0, то y > 0 при 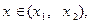y < 0 при

2-й случай. Если D = 0, тогда уравнение имеет единственное решение или два равных корня:

График квадратной функции, в этом случае, имеет только одну точку пересечения с осью OX (см. рис. 26).

Рис. 26

Замечаем, что если a > 0, тогда трехчлен (y) принимает положительные значения при всех значениях x, кроме и не принимает отрицательных значений;

если a < 0, тогда трехчлен (y) принимает отрицательные (y < 0) значения при всех значениях x, кроме и не принимает положительных значений.

3-й случай. Если D < 0, тогда уравнение не имеет действительных корней.

График функции не будет пересекать ось OX и при a > 0 функция принимает при всех x только положительные значения (y > 0), а при a < 0 только отрицательные значения (y < 0) (см. рис. 27).

Рис. 27

Определение. Квадратное уравнение называется приведенным, если коэффициент при равен 1, т. е. a = 1.

В этом случае, уравнение можно записать в виде:

Дата добавления: 2015-04-24