Использование однородного уравнения в системе

Выражение 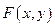называется однородным по х и у, если оно представляет собой многочлен, в каждое слагаемое которого входят только целые неотрицательные степени переменных х и у и их суммарная степень одна и та же во всех слагаемых.

Например, однородными являются следующие многочлены: .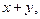

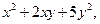
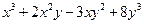Уравнение называется однородным, если оно имеет вид 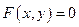, в котором 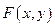– это однородное выражение по х и у.

Например, однородными являются следующие уравнения: , , .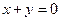

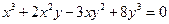Однородное уравнение всегда имеет тривиальное решение .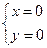

Другие его решения можно найти, если в этом уравнении перейти к отношению неизвестных делением обеих частей равенства на у ².

ПРИМЕРЫ

1. Решим систему .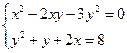

Решение

Первое уравнение системы является однородным по неизвестным х и у.

Поработаем с ним отдельно, записав сначала его тривиальное решение, а затем разделив обе части уравнения на :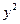

,

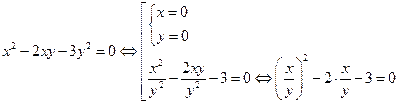переходом к отношению неизвестных получили квадратное уравнение относительно этого отношения 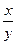; решаем это квадратное уравнение:

, .

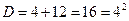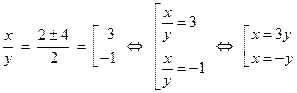Возвращаемся в исходную систему, используя результаты работы с однородным уравнением:

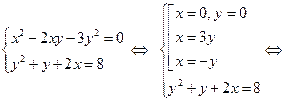
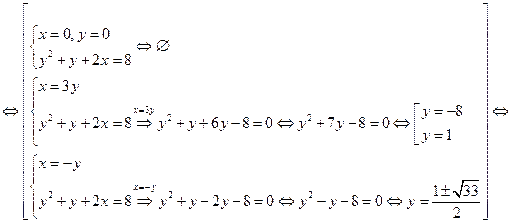
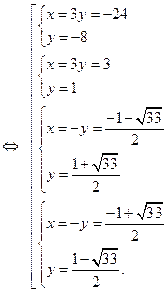
Всего система имеет четыре решения, которые подтверждаем проверкой, подставляя каждое решение в исходную систему.

Проверка:

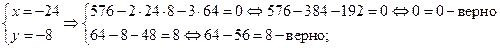
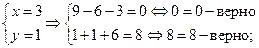
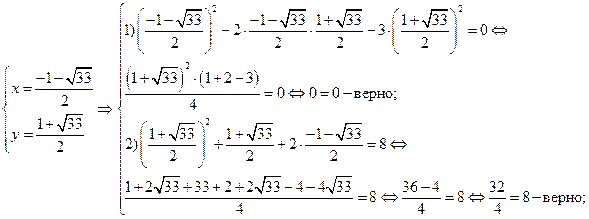
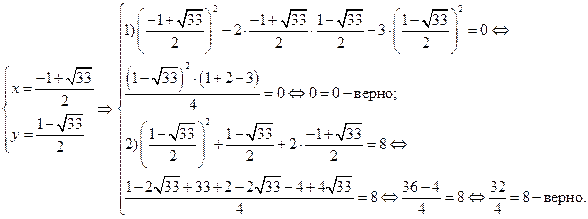
Ответ: , , , .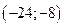

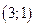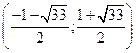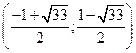2. Решим систему .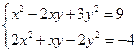

Решение

В данной системе можно получить однородное уравнение, если алгебраическим сложением уравнений получить уравнение с правой частью, равной нулю:

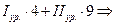
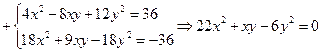– однородное уравнение.

Чтобы в пару к однородному уравнению получить более простое уравнение, сделаем ещё одно алгебраическое сложение уравнений с целью исключить произведение ху:

.

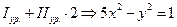В результате данная система заменится на равносильную систему, в которой есть однородное уравнение:

.

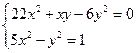Тривиальное решение 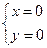однородного уравнения второму уравнению системы не удовлетворяет, поэтому это тривиальное решение можно не рассматривать, а перейти в однородном уравнении сразу к отношению 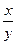делением обеих частей уравнения на .

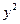В результате вновь получаем систему, равносильную данной:

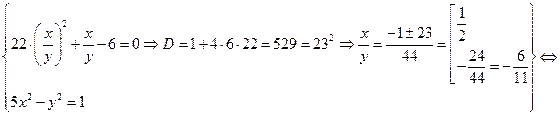
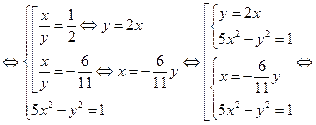
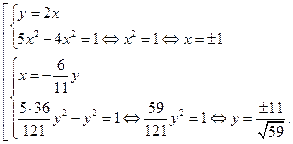
Система имеет 4 решения, подтверждаемых проверкой.

Ответ: , , , .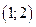

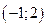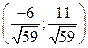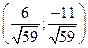Дата добавления: 2015-04-24