Свободные затухающие колебания в электрическом колебательном контуре

Дифференциальное уравнение свободных затухающих колебаний заряда в контуре (при R¹0) имеет вид (см. (143.2))

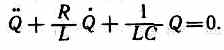
Учитывая выражение (142.2) и принимая коэффициент затухания

d= R/ (2L), (146.11)

дифференциальное уравнение (143.2) можно записать в идентичном уравнению (146.1) виде

Из выражений (146.1) и (146.5) вытекает, что колебания заряда совершаются по закону

Q =Q_me^-dtcos((wt+j) (146.12)

с частотой, согласно (146.4),

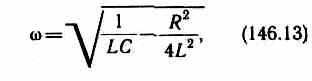
меньшей собственной частоты контура w₀ (см. (143.4)). При R= 0формула (146.13) переходит в (143.4).

Логарифмический декремент затуха­ния определяется формулой (146.7), а до­бротность колебательного контура (см. (146.8))

В заключение отметим, что при увели­чении коэффициента затухания d период затухающих колебаний растет и при d=w₀ обращается в бесконечность, т. е. движе­ние перестает быть периодическим. В дан­ном случае колеблющаяся величина асим­птотически приближается к нулю, когда t ®¥. Процесс не будет колебательным. Он называется апериодическим.

Огромный интерес для техники пред­ставляет возможность поддерживать коле­бания незатухающими. Для этого необхо­димо восполнять потери энергии реальной колебательной системы. Особенно важны и широко применимы так называемые ав­токолебания — незатухающие колебания, поддерживаемые в диссипативной системе за счет постоянного внешнего источника энергии, причем свойства этих колебаний определяются самой системой.

Автоколебания принципиально отлича­ются от свободных незатухающих колеба­ний, происходящих без действия сил, а также от вынужденных колебаний (см. §147), происходящих под действием периодической силы. Автоколебательная система сама управляет внешними воз­действиями, обеспечивая согласованность поступления энергии определенными пор­циями в нужный момент времени (в такт с ее колебаниями).

Примером автоколебательной системы могут служить часы. Храповой механизм подталкивает маятник в такт с его колеба­ниями. Энергия, передаваемая при этом маятнику, берется либо за счет раскручи-

вающейся пружины, либо за счет опуска­ющегося груза. Колебания воздуха в ду­ховых инструментах и органных трубах также возникают вследствие автоколеба­ний, поддерживаемых воздушной струей. Автоколебательными системами явля­ются также двигатели внутреннего сгора­ния, паровые турбины, ламповый генера­тор и т. д.

Дата добавления: 2015-04-24