Резонанс напряжений. Реактивным сопротивлением

Реактивным сопротивлением.

Рассмотрим частный случай, когда в цепи отсутствует конденсатор. В данном случае падения напряжений U_R и U_L в сумме равны приложенному напряже­нию U. Векторная диаграмма для данного случая представлена на рис. 217, из кото­рого следует, что

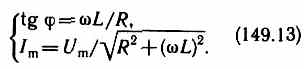
Выражения (149.9) и (149.10) совпадают с (149.13), если в них 1/(wС) = 0, т. е. С=¥. Следовательно, отсутствие конден­сатора в цепи означает С=¥, а не С=0. Данный вывод можно трактовать сле­дующим образом: сближая обкладки конденсатора до их полного соприкоснове­ния, придем к цепи, в которой конденсатор отсутствует (расстояние между обкладками стремится к нулю, а емкость — к бес­конечности; см. (94.3)).

Если в цепи переменного тока, содержа­щей последовательно включенные конден­сатор, катушку индуктивности и резистор (см. рис. 216),

wL= 1/(wС), (150.1)

то угол сдвига фаз между током и на­пряжением (149.9) обращается в нуль (j=0), т. е. изменения тока и напряжения происходят синфазно. Условию (150.1) удовлетворяет частота

w_рез=l/ÖLC. (150.2)

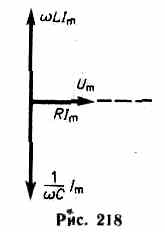
В данном случае полное сопротивление цепи Z (149.12) становится минимальным, равным активному сопротивлению R цепи, и ток в цепи определяется этим сопро­тивлением, принимая максимальные (воз­можные при данном U_m) значения. При этом падение напряжения на активном сопротивлении равно внешнему напряже­нию, приложенному к цепи (U_R=U), а па­дения напряжений на конденсаторе (U_C) и катушке индуктивности (U_L) одинаковы по амплитуде и противоположны по фазе. Это явление называется резонансом на­пряжений (последовательным резонан­сом), а частота (150.2) — резонансной частотой. Векторная диаграмма для резо­нанса напряжений приведена на рис.218, а зависимость амплитуды силы тока от w уже была дана на рис. 211.

В случае резонанса напряжений

(U_L)_реэ=(U_C)_рез,

поэтому, подставив в эту формулу значе­ния резонансной частоты и амплитуды на­пряжений на катушке индуктивности

и конденсаторе, получим

где Q — добротность контура, определяе­мая выражением (146.14). Так как до­бротность обычных колебательных конту­ров больше единицы, то напряжение как на катушке индуктивности, так и на кон­денсаторе превышает напряжение, прило­женное к цепи. Поэтому явление резонан­са напряжений используется в технике для усиления колебания напряжения какой-либо определенной частоты. Например, в случае резонанса на конденсаторе мож­но получить напряжение с амплитудой QU_m (Q в данном случае — добротность контура), которая может быть значительно больше U_m). Это усиление напряжения возможно только для узкого интервала частот вблизи резонансной частоты кон­тура, что позволяет выделить из многих сигналов одно колебание определенной частоты, т. е. на радиоприемнике настро­иться на нужную длину волны. Явление резонанса напряжений необходимо учиты­вать при расчете изоляции электрических линий, содержащих конденсаторы и ка­тушки индуктивности, так как иначе мо­жет наблюдаться их пробой.

Дата добавления: 2015-04-24