Статистический подход определения количества информации

Количество информации. Единицы измерения информации

Методы оценки количества информации

Количеством информации называют числовую характеристику сигнала, отражающую ту степень неопределенности (неполноту знаний), которая исчезает после получения сообщения в виде данного сигнала. Если в результате получения сообщения достигается полная ясность в каком-то вопросе, говорят, что была получена полная или исчерпывающая информация и необходимости в получении дополнительной информации нет. И, наоборот, если после получения сообщения неопределенность осталась прежней, значит, информации получено не было.

Приведенные рассуждения показывают, что между понятиями информация, неопределенность и возможность выбора существует тесная связь. Так, любая неопределенность предполагает возможность выбора, а любая информация, уменьшая неопределенность, уменьшает и возможность выбора. При полной информации выбора нет. Частичная информация уменьшает число вариантов выбора, сокращая тем самым неопределенность.

С середины XX века информация является общенаучным понятием, которое включает в себя: обмен сведениями между людьми, человеком и автоматом, автоматом и автоматом; обмен сигналами в животном и растительном мире; передачу признаков от клетки к клетке, от организма к организму и т. д.

Для того чтобы оценить и измерить количество информации применяются различные подходы. Среди них выделяются статистический (энтропийный) подход, семантический, прагматический, структурный (объёмный), и алгоритмический. Исторически наибольшее развитие получил статистический подход.

Статистический подход изучается в разделе кибернетики, называемом теорией информации. Его основоположником считается К. Шеннон, опубликовавший в 1948 г. свою математическую теорию связи. Шенноном было введено понятие количества информации как меры неопределенности состояния системы, снимаемой при получении информации. Количественно выраженная неопределенность состояния получила название энтропии по аналогии с подобным понятием в статистической механике. При получении информации уменьшается неопределенность, т. е. энтропия, системы. Очевидно, что чем больше информации получает наблюдатель, тем больше снимается неопределенность, и энтропия системы уменьшается. При энтропии, равной нулю, о системе имеется полная информация, и наблюдателю она представляется целиком упорядоченной. Таким образом, получение информации связано с изменением степени неосведомленности получателя о состоянии этой системы,

Информация о состояниях системы передается получателю в виде сообщений, которые могут быть представлены в различной синтаксической форме, например в виде кодовых комбинаций. Если код двоичный, т.е. используется в алфавите лишь два символа (0 и 1), то говорят о бинарных системах.

Например, человек бросает монету и наблюдает, какой стороной она упадет. Обе стороны монеты равноправны, поэтому одинаково вероятно, что выпадет одна или другая сторона. Такой ситуации приписывается неопределенность, характеризуемая двумя возможностями состояниями. После того, как монета упадет и поступает сигнал о стороне, на которую она упала, достигается полная ясность и неопределенность исчезает. Приведенный пример относится к группе событий, применительно к которым может быть поставлен вопрос типа «да-нет».

Количество информации, необходимое для однозначного определения одного из двух равновероятных событий, называется битом (англ. bit – сокращенное от binary digit – двоичная единица). Бит – минимальная единица количества информации в бинарных системах, т.к. получить информацию меньшую, чем 1 бит, невозможно. При получении информации в 1 бит неопределенность уменьшается в 2 раза.

В качестве других моделей получения такого же количества информации могут выступать электрическая лампочка, двухпозиционный выключатель, магнитный сердечник, диод и т.п. Включенное состояние этих объектов обозначают цифрой 1, а выключенное – цифрой 0.

Рассмотрим систему из двух персональных компьютеров, которые независимо друг от друга могут быть включены или выключены. Для такой системы возможны следующие 4 состояния. При этом каждый и двух компьютеров может находиться в состояниях:

Персональный компьютер № 1 может иметь состояния: 0 0 1 1.

Персональный компьютер № 2 может иметь состояния: 0 1 0 1.

Чтобы получить полную информацию о состоянии системы, необходимо задать два вопроса типа «да-нет» – по персональному компьютеру 1 и персональному компьютеру 2 соответственно. В этом случае количество информации, содержащейся в сообщении о состоянии данной системы, определяется уже в 2 бита, при числе возможных состояний системы – 4. Если взять три персональных компьютера, то необходимо задать уже три вопроса и получить 3 бита информации. Количество состояний такой системы равно – 8 и т. д.

Связь между количеством информации и логарифмом числа возможных равновероятных состояний бинарной системы устанавливается как линейная по формуле Хартли:

I = log2 N,

(2.1)

где I – количество информации в битах; N – число возможных равновероятных состояний.

Эту же формулу можно представить иначе

.

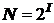(2.2)

Группа из 8 битов информации называется байтом. Если бит – минимальная единица информации, то байт ее основная единица. Существуют производные единицы информации: килобайт (Кбайт, Кбт), мегабайт (Мбайт, Мбт), гигабайт (Гбайт, Гбт), терабайт (Тбайт, Тбт), петабайт (Пбайт, Пбт).

1 Кбт = 1024 байта = 2¹⁰ (1024) байтов.

1 Мбт = 1024 Кбайта = 2²⁰ (1024 • 1024) байтов.

1 Гбт = 1024 Мбайта = 2³⁰ (1024 • 1024 • 1024) байтов.

1 Тбт = 1024 Гбайта = 2⁴⁰ (1024 • 1024 • 1024 • 1024) байтов.

1 Пбт = 1024 Тбайта = 2⁵⁰ (1024 • 1024 • 1024 • 1024• 1024) байтов.

Эти единицы часто используют для указания объема памяти компьютера.

Пример 1. Пусть имеется колода карт, содержащая 32 различные кары. Мы вытаскиваем одну карту из колоды. Какое количество информации мы получим?

Количество возможных вариантов выбора карты из колоды – 32 (N = 32) и все события равновероятны. Воспользуемся формулой определения количества информации для равновероятных событий I = log₂N = log₂32 = 5, (32 = 2^I; 2⁵ = 2^I; отсюда I = 5 бит).

Если количество возможных вариантов N является целой степенью числа 2, то производить вычисления по формуле N = 2^I достаточно легко. Если же количество возможных вариантов не является целой степенью числа 2, то необходимо воспользоваться инженерным калькулятором, формулу I = log₂N представить как 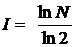и произвести необходимые вычисления.

Пример 2. Какое количество информации можно получить при угадывании числа из интервала от 1 до 11?

В этом примере N = 11. Число 11 не является степенью числа 2, поэтому воспользуемся инженерным калькулятором и произведем вычисления для определения I (количества информации). I = 3,45943 бит.

При использовании для небинарных систем в качестве основания логарифма другого числа, например 10, единицы измерения информации могут быть десятичными, или дитами. Десятичная единица информации составляет примерно 3,33 бита.

Иногда удобно применять натуральное основание логарифма e при определении количества информации. В этом случае получающиеся единицы информации называются натуральными или натами. Переход от основания a к основанию b требует лишь умножения на .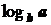

Очень часто в жизни мы сталкиваемся с событиями, которые имеют разную вероятность реализации. Например:

1. Когда сообщают прогноз погоды, то сведения о том, что будет дождь, более вероятны летом, а сообщение о снеге – зимой.

2. Если вы – лучший студент в группе, то вероятность сообщения о том, что за контрольную работу вы получите 5, больше, чем вероятность получения двойки.

3. Если в мешке лежит 10 белых шаров и 3 черных, то вероятность достать черный шар меньше, чем вероятность вытаскивания белого.

Как вычислить количество информации в сообщении о таком событии?

Если система обладает дискретными состояниями (т.е. переходит из состояния в состояние скачком), их количество равно N, а вероятность нахождения системы в каждом из состояний 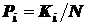, где 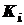– величина, показывающая, сколько раз произошло интересующее нас событие, то согласно теореме Шеннона количество индивидуальной информации события 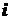определяется соотношением

.

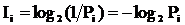(2.3)

Более удобно пользоваться средним значением количества информации, приходящимся на данное событие

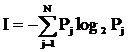
(2.4)

где 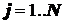. При равновероятных выборах все 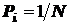мы имеем прежнюю формулу Хартли .

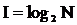Пример 3. В мешке находятся 20 шаров. Из них 15 белых и 5 красных. Какое количество информации несет сообщение о том, что достали: а) белый шар; б) красный шар. Сравните ответы.

1. Найдем вероятность того, что достали белый шар: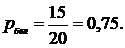

2. Найдем вероятность того, что достали красный шар: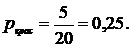

3. Найдем количество информации в сообщении о вытаскивании белого шара: 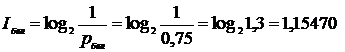бит.

4. Найдем количество информации в сообщении о вытаскивании красного шара: 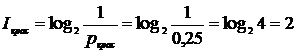бит.

Количество информации в сообщении о том, что достали белый шар, равно 1, 1547 бит. Количество информации в сообщении о том, что достали красный шар, равно 2 бит.

При сравнении ответов получается следующая ситуация: вероятность вытаскивания белого шара была больше, чем вероятность красного шара, а информации при этом получилось меньше. Это не случайность, а закономерная, качественная связь между вероятностью события и количеством информации в сообщении об этом событии.

Дата добавления: 2015-04-25