
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Фундаментальная числовая последовательность
|
|
|
|
Подпоследовательность числовой последовательности. Частичный предел.
def: Няхай 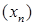 ёсць некаторая лікавая паслядоўнасць, а
ёсць некаторая лікавая паслядоўнасць, а 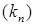 адвольная нарастальная паслядоўнасць натуральных лікаў, г.зн.
адвольная нарастальная паслядоўнасць натуральных лікаў, г.зн.  , прычым
, прычым  Паслядоўнасць
Паслядоўнасць 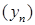 , агульны элемент якой
, агульны элемент якой 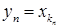 , г.зн. паслядоўнасць
, г.зн. паслядоўнасць  называюць падпаслядоўнасцю лікавай паслядоўнасці
называюць падпаслядоўнасцю лікавай паслядоўнасці 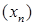 . Такім чынам, калі з паслядоўнасці
. Такім чынам, калі з паслядоўнасці 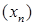 выбраць элементы з нумарамі
выбраць элементы з нумарамі  , то атрымаецца падпаслядоўнасць
, то атрымаецца падпаслядоўнасць  . Калі падпаслядоўнасць
. Калі падпаслядоўнасць  збежная, то яе ліміт называецца частковым лімітам паслядоўнасці
збежная, то яе ліміт называецца частковым лімітам паслядоўнасці 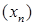 .
.
def: Лікавая паслядоўнасць  называецца фундаментальнаю, калі
называецца фундаментальнаю, калі
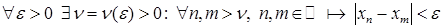 ,
,
або інакш
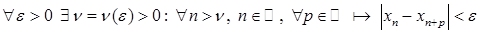 .
.
12. Предел функции в точке и на 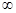 , бесконечный предел. Односторонние пределы
, бесконечный предел. Односторонние пределы
def: Лік 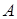 называюць лімітам функцыі
называюць лімітам функцыі 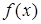 у пункце
у пункце 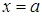 , калі гэтая функцыя вызначана ў некаторай праколатай акрузе пункта
, калі гэтая функцыя вызначана ў некаторай праколатай акрузе пункта  (у самім пункце
(у самім пункце  функцыя можа быць і нявызначанай) і
функцыя можа быць і нявызначанай) і 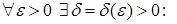
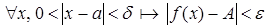 , або
, або 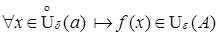 .
.
Гэтае азначэнне называюць азначэннем паводле Кашы або
на мове “  ”. Пры гэтым пішуць
”. Пры гэтым пішуць 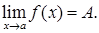
def: Лік 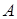 называюць правабаковым (левабаковым) лімітам функцыі
называюць правабаковым (левабаковым) лімітам функцыі 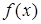 у пункце
у пункце 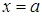 , калі
, калі 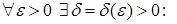
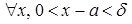 (
(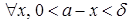 )
) 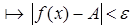 , што абазначаюць адпаведна
, што абазначаюць адпаведна 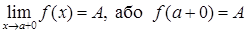 (
( ). Пры гэтым кажуць таксама, што функцыя
). Пры гэтым кажуць таксама, што функцыя 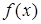 мае ліміт
мае ліміт 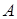 , калі
, калі  імкнецца да
імкнецца да  справа (злева)
справа (злева)
def: Калі функцыя 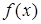 вызначана
вызначана 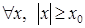 і
і 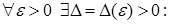
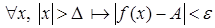 , то кажуць, што лік
, то кажуць, што лік 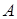 ёсць ліміт функцыі
ёсць ліміт функцыі 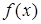 пры
пры 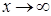 і пішуць
і пішуць  . Калі
. Калі 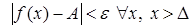 , то пішуць
, то пішуць 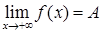 . Калі
. Калі 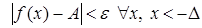 , то пішуць
, то пішуць  .
.
def: Калі функцыя 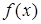 вызначана ў праколатай акрузе пункта
вызначана ў праколатай акрузе пункта  і
і  , то кажуць, што функцыя
, то кажуць, што функцыя 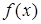 ёсць бясконца вялікая, або мае сваім лімітам
ёсць бясконца вялікая, або мае сваім лімітам  пры
пры  , і пішуць
, і пішуць 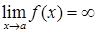 . Калі
. Калі 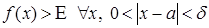 , то пішуць
, то пішуць  (пры гэтым
(пры гэтым 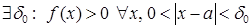 ). Калі
). Калі 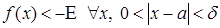 , то пішуць
, то пішуць 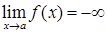 (пры гэтым
(пры гэтым  ).
).
|
|
|
|
|
Дата добавления: 2015-03-29; Просмотров: 418; Нарушение авторских прав?; Мы поможем в написании вашей работы!