Локальный экстремум функции

Дифференциал. Инвариантность формы дифференциала

Производная функции, односторонние производные.

def. Няхай функцыя 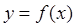вызначана ў акрузе пункта . Калі існуе 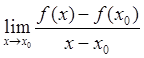, то гэты ліміт называецца вытворнай функцыі 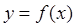у пункце .

def. Калі існуюць і 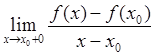то іх называюць адпаведна левабаковай і правабаковай вытворнымі функцыі 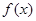у пункце 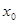і абазначаюць адпаведна 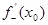і .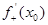

З уласцівасцяў лімітаў вынікае: функцыя 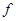мае вытворную ў пункце , калі і толькі калі яна мае левабаковую і правабаковую вытворныя: 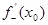= 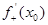,прычым 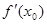= = 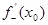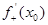. 20. Геометрический смысл производной

вытворная 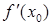функцыі пункце 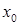ёсць вуглавы каэфіцыент датычнай да графіка функцыі ў пункце .

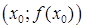def. Галоўную лінейную частку прыросту дыферанцавальнай ў пункце 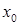функцыі (гл. (1)) называюць дыферэнцыялам функцыі і абазначаюць .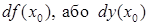

Такім чынам,

Тэарэма 2 (інварыянтавасць формы дыферэнцыяла). Дыферэнцыял функцыі мае адзін і той самы выгляд 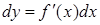не гледзячы на тое, ці ёсць x незалежная зменная, ці х – дыферэнцавальная функцыя якой-небудзь іншай зменнай.

□ Няхай 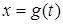ёсць дыферэнцавальная функцыя зменнай t. Тады складаная функцыя мае вытворную 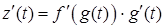, а таму

. ■

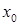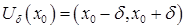def. Няхай існуе –акруга пункта , , ў якой вызначана функцыя 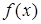і . Тады кажуць, што функцыя 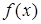мае ў пункце 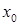лакальны максімум (мінімум). Лакальны максімум і лакальны мінімум аб’ядноўваюць агульным тэрмінам лакальны экстрэмум.

23. Первообразная и неопределённый интеграл.

def. Дыферэнцавальная на інтэрвале Х функцыя называецца першаіснаю для функцыі 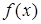на Х, калі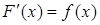

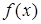def. Калі ёсць першаісная для на інтэрвале Х, то сукупнасць 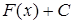першаісных для 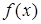называюць нявызначаным інтэгралам ад функцыі на Х і абазначаюць

.

24. Интегральная сумма и определённый интеграл для функции 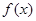на отрезке .

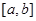Няхай функцыя вызначана на адрэзку (магчыма разрыўная, магчыма непарыўная, магчыма недыферэнцавальная, магчыма дыферэнцавальная ў пунктах адрэзка). Няхай 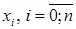– сукупнасць пунктаў гэтага адрэзка такіх, што . Мноства гэтых пунктаў назавем падзелам адрэзка і абазначым 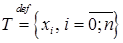. Адрэзкі назавем адрэзкамі падзелу 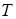, або частковымі адрэзкамі адрэзка .

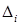Абазначым праз даўжыні адрэзкаў . Лік 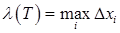назавем дробнасцю падзелу 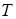. Мноства пунктаў будзем называць выбаркай з адрэзка . Суму будзем называць інтэгральнаю сумай для функцыі 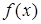пры зададзеным падзеле 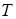і фіксаванай выбарцы .

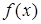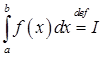def. Лік I называюць вызначаным інтэгралам функцыі на адрэзку і абазначаюць , калі

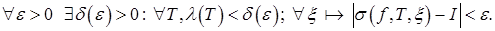(1)

Пры гэтым таксама кажуць, што існуе ліміт 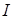інтэгральных сумаў пры , і гэты ліміт не залежыць ні ад падзелу 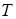, ні ад выбаркі і пішуць

Дата добавления: 2015-03-29