
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Емкостный элемент в цепи синусоидального тока
|
|
|
|
Пусть к цепи рис. 2.12 действует синусоидальное напряжение

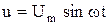
или в комплексной форме
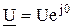 .
.
Как показано в разделе 2.2., ток в цепи с емкостью пропорционален скорости изменения напряжения, т.е. 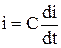 , т.е.
, т.е.
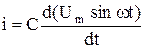 . .
| (2.35) |
После дифференцирования 2.35 получаем:
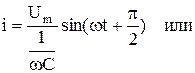 , ,
| (2.36) |
или в комплексной форме
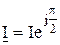 . .
| (2.37) |
Как видно из 2.36 ток в идеальной емкостной цепи так же, как и напряжение изменяется по синусоидальному закону и опережает напряжение по фазе на одну четверть периода. Амплитуда тока связана с амплитудой напряжения соотношением:
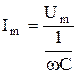 . .
| (2.38) |
Поделив обе части 2.38 на 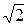 получим:
получим:
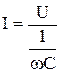 , ,
| (2.39) |
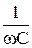 – имеет размерность сопротивления, обозначается ХС и называется емкостным реактивным сопротивлением.
– имеет размерность сопротивления, обозначается ХС и называется емкостным реактивным сопротивлением.
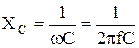 . .
| (2.40) |
Из 2.40 видно, что емкостное сопротивление уменьшается с увеличением частоты.
Поделив комплекс напряжения на комплекс тока, получим
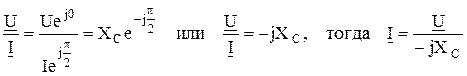 , ,
| (2.41) |
– jXc – называется комплексом емкостного сопротивления, он может принимать только отрицательные значения.
Выражения 2.38, 2.39, 2.41 представляют собой закон Ома для идеальной емкостной цепи соответственно для амплитудных и действующих значений напряжения и тока, а также в комплексной форме.
 В соответствии с комплексами напряжения и тока векторная диаграмма идеальной емкостной цепи построена на рис. 2.13.
В соответствии с комплексами напряжения и тока векторная диаграмма идеальной емкостной цепи построена на рис. 2.13.
Мгновенное значение мощности qC этой цепи равно произведению мгновенных значений напряжения и тока
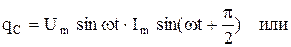
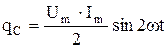 , т.е. , т.е.
| (2.42) |
мгновенная мощность в емкостной цепи также как ток и напряжение есть синусоидальная величина, изменяющаяся с удвоенной частотой по отношению к току и напряжению. Волновые диаграммы напряжения, тока и мощности, приведенные на рис. 2.14, показывают, что мгновенная мощность положительна только в нечетные четверти периода, когда ток и напряжение имеют одинаковое направление. В эти промежутки времени энергия от источника поступает в приемник, где накапливается в электрическом поле.
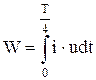 , ,
| (2.43) |
а т.к. i=C 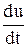 , то
, то

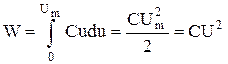 . (2.44)
. (2.44)
В четные четверти периода, когда напряжение и ток имеют противоположные направления, мгновенная мощность отрицательна. Это означает, что энергия, накопленная в электрическом поле приемника, возвращается к источнику. Таким образом, при работе идеального емкостного приемника энергия циркулирует между источником и электрическим полем приемника, а преобразования ее в другие виды не происходит, поэтому средняя мощность за период равна нулю. Такая цепь называется емкостной реактивной.
2.9. Последовательная цепь элементов R-L-C при синусоидальном токе.
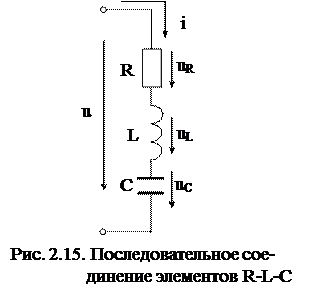 Пусть в цепи рис. 2.15 протекает ток
Пусть в цепи рис. 2.15 протекает ток
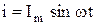 (2.45)
(2.45)
или в комплексной форме
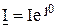 . (2.46)
. (2.46)
Тогда, напряжения на элементах цепи, как показано в разделах 2.6 – 2.8 будут описываться следующими уравнениями:
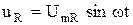
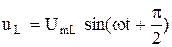 (2.47)
(2.47)
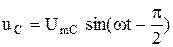
или в комплексной форме
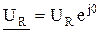 , ,
| |
 , ,
| (2.48) |
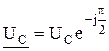 . .
|
На основании второго закона Кирхгофа комплекс напряжения на зажимах цепи равен сумме комплексов напряжений на отдельных участках
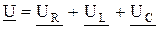 , ,
| (2.49) |
а на основании закона Ома для отдельных участков цепи можно записать
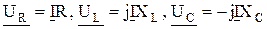 . .
|
Подставим U R , U L и U C в 2.49 и получим
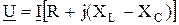 , ,
|
решая последнее уравнение относительно комплекса тока получим
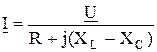 . .
| (2.50) |
Выражение 2.50 представляет собой закон Ома для последовательной цепи элементов R-L-C.
Знаменатель формулы 2.50 обозначается Z и называется комплексом полного сопротивления
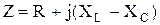 . .
| (2.51) |
Запишем комплекс полного сопротивления в показательной форме
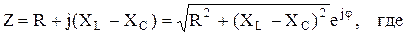
|
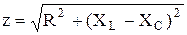 – модуль комплекса полного сопротивления;
– модуль комплекса полного сопротивления;
 – аргумент комплекса полного сопротивления
– аргумент комплекса полного сопротивления
 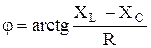 . .
| (2.52) |
Подставляя комплекс полного сопротивления в показательной форме в 2.50 и решая его относительно комплекса напряжения будем иметь
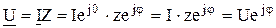 , ,
|
 т.е. приложенное к зажимам цепи напряжение сдвинуто по фазе относительно вектора тока на некоторый угол
т.е. приложенное к зажимам цепи напряжение сдвинуто по фазе относительно вектора тока на некоторый угол 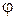 , величина которого зависит от соотношения сопротивлений элементов цепи.
, величина которого зависит от соотношения сопротивлений элементов цепи.
Как видно из 2.52, если ХL > XC, то 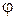 > 0, а напряжение будет опережать ток на угол
> 0, а напряжение будет опережать ток на угол 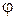 , цепь будет носить индуктивный характер
, цепь будет носить индуктивный характер
u= Umsin (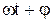 )
)
Если XL < XC, то 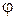 < 0 и напряжение будет отставать от тока на угол
< 0 и напряжение будет отставать от тока на угол 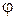
u= Umsin (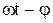 ),
),
а цепь будет носить емкостный характер.
Наконец, если XL = XC, то 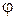 = 0, т.е. напряжение будет совпадать по фазе с током
= 0, т.е. напряжение будет совпадать по фазе с током
u= Umsin  ,
,
а цепь будет носить активный характер.
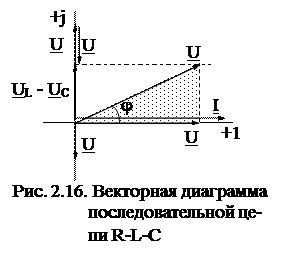
В соответствии с уравнениями 2.46, 2.48 на рис. 2.16 построена векторная диаграмма в предположении, что XL > XC. Выделенный на диаграмме треугольник называется треугольником напряжений, из рассмотрения которого вытекает
 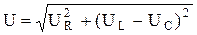 , ,
| (2.53) |
а также
 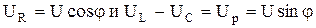 , ,
| (2.54) |
UL – UC – называется реактивным напряжением.
 Поделив все стороны треугольника напряжений на ток, можно получить треугольник сопротивлений (рис. 2.17), из которого могут быть получены соотношения, аналогичные соотношениям, полученным из треугольника напряжений.
Поделив все стороны треугольника напряжений на ток, можно получить треугольник сопротивлений (рис. 2.17), из которого могут быть получены соотношения, аналогичные соотношениям, полученным из треугольника напряжений.
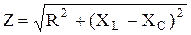 и
и
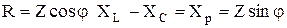 . .
| (2.55) |
Если все стороны треугольника напряжений умножить на ток, получим треугольник мощностей (рис. 2.18).
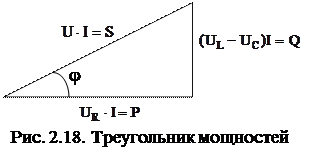 Гипотенуза этого треугольника характеризует установленную мощность источника, она называется полной мощностью
Гипотенуза этого треугольника характеризует установленную мощность источника, она называется полной мощностью
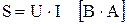 . (2.56)
. (2.56)
По величине полной мощности выбирают все элементы электротехнических устройств и аппаратов.
Активная мощность
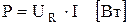
| (2.57) |
характеризует процессы необратимого преобразования электрической энергии в другие виды. Нетрудно видеть из рис. 2.18, что активная мощность составляет часть полной мощности
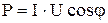 . .
| (2.58) |
Реактивная мощность
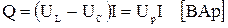
| (2.59) |
характеризует процессы обмена энергией между источником и полями приемников. Она составляет другую часть полной мощности
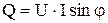 . .
| (2.60) |
Все три мощности, как это видно из рис. 2.17 связаны квадратурой
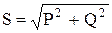 . .
| (2.61) |
Полную мощность S можно рассматривать как модуль величины, называемой комплексной мощностью 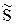 .
.
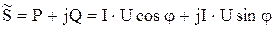 , ,
| |
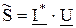 , ,
| (2.62) |
где 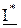 сопряженный комплекс тока.
сопряженный комплекс тока.
Из треугольника мощностей следует, что
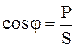 , ,
| (2.63) |
т.е. он показывает, какая доля мощности источника необратимо преобразуется в другие виды, поэтому он называется коэффициентом мощности.
|
|
|
|
|
Дата добавления: 2015-05-06; Просмотров: 2630; Нарушение авторских прав?; Мы поможем в написании вашей работы!