Параллельная цепь элементов R-L-C при синусоидальном токе

Пусть к цепи рис. 2.19 подведено синусоидальное напряжение

u = U_msin ,

или в комплексной форме

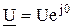
На основании первого закона Кирхгофа комплекс тока в неразветвленной части цепи равен сумме комплексов токов в ветвях, т.е.

I = I _R + I _L + I _C, (2.66)

а на основании закона Ома комплексы токов в ветвях

.

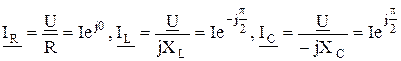Подставляя комплексы токов в ветвях цепи в 2.66, получим

,

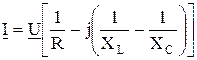(2.67)

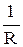= g называется активной проводимостью;

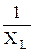= b_L – реактивной индуктивной проводимостью;

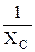= b_C – реактивной емкостной проводимостью цепи.

Подставив значения проводимостей в 2.67 получим:

,

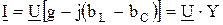(2.68)

Y= g – j(b_L – b_C) называется комплексом полной проводимости цепи; запишем ее в показательной форме

.

(2.69)

Модуль комплекса полной проводимости

,

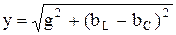(2.70)

аргумент комплекса полной проводимости

.

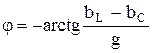(2.71)

Подставляя комплексы напряжения и полной проводимости в 2.68 получим

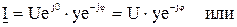
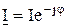,	(2.72)

т.е. вектор тока в неразветвленной части цепи сдвинут относительно вектора напряжения на угол 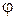, величина которого определяется параметрами цепи.

Если b_L – b_C > 0, то 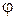< 0 и ток отстает от напряжения на угол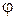

i=I_msin(),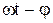

цепь в этом случае носит индуктивный характер;

если b_L – b_C < 0, то 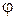> 0, а ток опережает напряжение на угол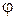

i=I_msin(),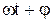

цепь в этом случае носит емкостный характер;

если b_L = b_C, то 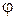= 0 и ток совпадает по фазе с напряжением

i=I_msin ,

а цепь носит активный характер.

Из 2.72 следует, что

.

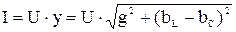(2.73)

Выражение 2.73 есть закон Ома для действующих значений напряжения и тока.

В соответствии со значениями комплексов напряжения и токов в ветвях на рис. 2.20 построена векторная диаграмма для случая индуктивной цепи, т.е когда b_L > b_C.

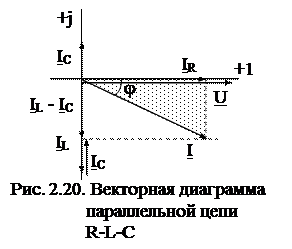Выделенный на диаграмме треугольник называется треугольником токов, из рассмотрения которого следуют формулы, широко используемые в практических расчетах:

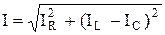, (2.74)

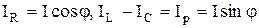. (2.75)

Разность между индуктивным током I_L и емкостным током I_C называется реактивным током и обозначается I_P.

Поделив все стороны треугольника токов на напряжение, получим треугольник проводимостей (рис. 2.21), из которого следует полученная ранее формула модуля комплекса полной проводимости

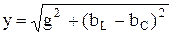
а также формулы активной и реактивной проводимостей

.

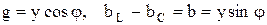(2.76)

Поскольку законы изменения токов и напряжений и их фазовые соотношения в последовательной и параллельной цепях одинаковы, то естественно, что идентичными будут и энергетические процессы, протекающие в них. Формулы для расчета мощностей в параллельной цепи будут такими же, что и для расчета в последовательной цепи.

Дата добавления: 2015-05-06