Индуктивный элемент в цепи синусоидального тока

Пусть к цепи рис. 2.9 подведено синусоидальное напряжение

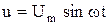
или в комплексной форме

.

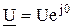Как показано в разделе 2.2 напряжение в цепи с индуктивностью пропорционально скорости изменения тока, т.е. 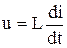, т.е.

или

.

(2.26)

После интегрирования 2.26 получим

или

(2.27)

т.е. ток в идеальной индуктивной цепи, так же как и напряжение, изменяется по закону синуса и отстает по фазе от напряжения на одну четверть периода. Амплитуда тока связана с амплитудой напряжения соотношением

.

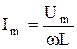(2.28)

Поделив обе части 2.28 на 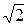получим

,

(2.29)

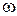L – имеет размерность сопротивления, обозначается X_L и называется индуктивным реактивным сопротивлением, т.к. , то

.

(2.30)

Нетрудно видеть, что индуктивное сопротивление растет с увеличением частоты.

Поделив комплекс напряжения на комплекс тока получим

,

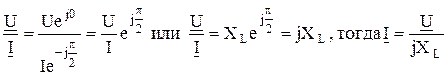(2.31)

jX_L – называется комплексом индуктивного сопротивления, он может принимать только положительные значения.

Выражения 2.28, 2.29 и 2.31 представляют собой закон Ома для идеальной индуктивной цепи соответственно для амплитудных, действующих значений напряжения и тока, а также в комплексной форме.

В соответствии с комплексами напряжения и тока, векторная диаграмма идеальной индуктивной цепи построена на рис. 2.10.

Мгновенное значение мощности q_L этой цепи равно произведению мгновенных значений тока и напряжения:

.

После преобразования получим

,

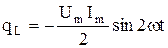(2.32)

т.е. мгновенная мощность в идеальной индуктивной цепи также как ток и напряжение есть синусоидальная величина, и изменяется с удвоенной частотой по отношению к току и напряжению. Волновые диаграммы напряжения, тока и мгновенной мощности, приведенные на рис. 2.11, показывают, что мгновенная мощность положительна только в четные четверти периода, когда ток и напряжение имеют одинаковое направление. В эти промежутки времени энергия от источника поступает в приемник, где накапливается в магнитном поле.

,

(2.33)

а т.к. 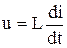, то

,

(2.34)

В нечетные периоды, когда напряжение и ток имеют противоположные направления, мгновенная мощность отрицательна. Это означает, что энергия, накопленная в магнитном поле приемника, возвращается источнику. Таким образом, при работе идеального индуктивного приемника энергия циркулирует между источником и магнитным полем приемника, а преобразования ее в другие виды не происходит, поэтому средняя мощность за период равна нулю. Такая цепь называется индуктивной реактивной.

Дата добавления: 2015-05-06