Методы изображения синусоидальных величин

Синусоидально изменяющиеся электрические величины можно изобразить аналитически с помощью уравнений с тригонометрическими функциями (см. формулы 2.4), графически в декартовых координатах и в виде вращающихся векторов на декартовой или комплексной плоскости.

При графическом построении положительные начальные фазы откладываются влево от начала координат, а отрицательные – вправо.

При изображении синусоидальных величин вращающимися векторами на декартовой плоскости из начала координат проводят векторы, равные амплитудам синусоидальных величин и вращают их в направлении, противоположном движению часовой стрелки с постоянной угловой скоростью 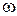. Фазовый угол отсчитывают от положительного направления горизонтальной оси.

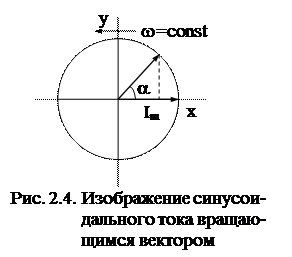За один период вектор повернется на 2 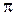радиан. Следовательно, 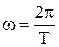, а т.к. 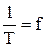, то

(2.14)

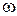– характеризует скорость изменения фазового угла и называется угловой частотой. При частоте f = 50 Гц 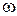= 314 рад / с.

Пусть к моменту времени t вектор повернется на угол 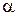, рис. 2.4. Тогда проекция вектора на вертикальную ось будет 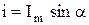и равна мгновенному значению тока в момент времени t. При равномерном вращении вектора в любой момент времени фазовый угол 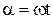и, следовательно

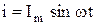
При частоте f= 50Гц

.

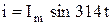(2.15)

Совокупность векторов, изображающих синусоидальные токи и напряжения одной частоты называется векторной диаграммой. При построении векторных диаграмм векторы удобно проводить для момента времени t = 0.

Применение векторных диаграмм при анализе работы цепей делает его проще и нагляднее и позволяет свести электротехническую задачу к расчету треугольников.

Пусть, например, в узле электрической цепи

i₁ = i₂ + i₃,

и .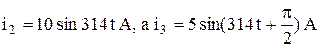

Тогда .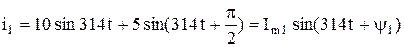

Нахождение амплитуды I_m1 и начальной фазы 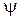₁ аналитически довольно сложно и значительно проще эти величины найти из векторной диаграммы, построенной в масштабе. Диаграмму строим для t = 0. Пусть в масштабном отрезке “ ” будет 1А.

На рис. 2.5 представлены начальные положения векторов токов, проекции которых на вертикальную ось дают мгновенные значения токов в момент времени t = 0. Вектор тока I_m1 находится геометрическим сложением векторов I_m2 и I_m3. Так как диаграмма строилась в масштабе, величина тока I_m1 может быть найдена умножением длины вектора I_m1 на масштаб, а начальная фаза 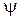₁ – измерена транспортиром.

При изображении вращающихся векторов синусоидальных величин на комплексной плоскости горизонтальную ось декартовых координат совмещают с осью действительных величин (+1) комплексной плоскости, тогда мгновенные значения синусоидальных величин получают на оси мнимых величин (+j). Положение конца вектора на комплексной плоскости соответствует точке на комплексной плоскости а + jb. С другой стороны, проекция вектора на ось действительных величин (+1) равна а, а на ось мнимых величин (+j) равна b. Следовательно вектор длиной 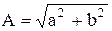рис. 2.6 (длина вектора называется модулем) можно условно, символически записать комплексным числом А = а+ jb. Вектор повернут относительно горизонтальной оси на угол .

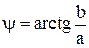Итак, синусоидально изменяющуюся величину можно изобразить вращающимся вектором, а вектор можно записать с помощью комплексного числа

,

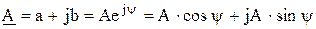(2.16)

следовательно, синусоидально изменяющиеся во времени величины можно описывать комплексными числами. Применение комплексных чисел дает возможность заменить геометрическое сложение или вычитание векторов на векторной диаграмме алгебраическими действиями над комплексными числами этих векторов. Комплексные числа векторов называются комплексами токов, напряжений, ЭДС. При записи их обозначения подчеркиваются снизу, в старой литературе в их обозначении ставится точка сверху, например 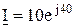или .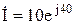

Дата добавления: 2015-05-06