Пример 1.7

На рис. 1.17 приведена исследуемая электрическая цепь.

Рисунок 1.17

На рис. 1.18 приведён направленный граф данной цепи с произвольно выбранными направлениями ветвей. На рис. 1.19 приведено одно из возможных деревьев графа.

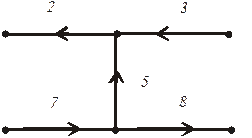
Рисунок 1.18 Рисунок 1.19

Подготовим листинг для решения данной задачи. Составим матрицы соединений и контуров, используя следующие правила.

Строки матрицы соединений соответствуют узлам графа за исключением нулевого узла. Столбцы соответствуют ветвям графа. Элементы матрицы равны: нулю, если данная ветвь не соединена с данным узлом; единице, если данная ветвь соединена с данным узлом и направлена от узла; минус единице, если данная ветвь соединена с данным узлом и направлена к узлу.

Строки матрицы контуров соответствуют связям дерева графа. Столбцы соответствуют ветвям графа. Элементы матрицы равны нулю, если данная ветвь не входит в контур, образованный данной связью; равны единице, если данная ветвь входит в контур, образованный данной связью, и направление её совпадает с направлением обхода контура, который берётся по направлению связи; равны минус единице, если данная ветвь входит в контур, образованный данной связью, а направление её не совпадает с направлением обхода контура.

Для графа (рис. 1.18) матрицы соединейний и контуров имеют следующий вид:

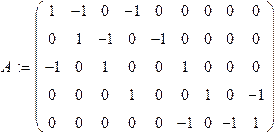
Зададимся параметрами элементов электрической цепи.

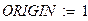
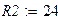
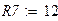
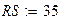
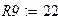
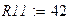
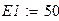
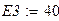
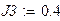
Подготовим диагональную матрицу сопротивлений ветвей.

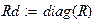
Подготовим матрицы источников и матрицу нулей.

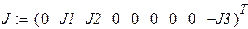
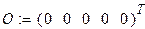
В системе уравнений используются столбцовые матрицы. Для компактности записи использовались строковые матрицы и оператор транспонирования.

Левую и правую части матричного уравнения (1.3) получим с помощью оператора слияния матриц по вертикали.

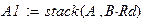
Найдём решение полученной системы линейных уравнений.

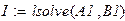
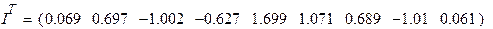
Чтобы убедиться, что токи найдены правильно, проверим баланс мощностей источников и приёмников электрической энергии в заданной цепи. Предварительно найдём токи в ветвях, содержащих резисторы, и напряжения на обобщённых ветвях.

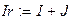
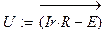
При определении напряжений использован оператор векторизации. Этот оператор предназначен для работы с массивами. Он берётся с панели Matrix и позволяет провести однотипную операцию над всеми элементами массива.

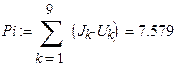
Найдём отдельно мощности источников ЭДС и источников тока, и суммарную мощность всех источников.

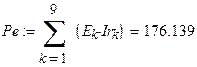
Найдём мощность, рассеиваемую резисторами электрической цепи.

Баланс мощностей выполняется.

Токи в резисторах R 11 и R 12 обратно пропорциональны их сопротивлению. Найдём их по формулам разброса подтекающего к узлу тока.

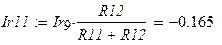
Остальные токи в ветвях с резисторами найдены выше и имеют следующие значения:

Знаки полученных токов позволяют указать на схеме электрической цепи их реальное направление. Погрешность суммы токов в резисторах R 11 и R 12 по сравнению с током Ir ₉ объясняется ограниченным количеством разрядов числа, выводимого на экран монитора. Точные значения можно получить следующим образом:

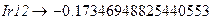
Необходимый оператор (стрелка) берётся с панели Symbolic.

В задачах анализа линейных электрических цепей система уравнений, составленная по законам Кирхгофа, используется редко из-за её громоздкости. В основном используют метод контурных токов или метод узловых потенциалов, которые позволяют составить более компактные системы уравнений. Рассмотрим использование этих методов в следующих разделах.

Результаты вычислений можно выводить в виде таблиц и в виде матриц. Для этого надо по траектории Format, Result Format, Display Options, Matrix display style установить Table либо Matrix. В противном случае программа выбирает стиль самостоятельно.

1.3. Использование метода контурных токов

В основе метода контурных токов лежит принцип суперпозиции. Задача анализа электрической цепи решается в два этапа. На первом этапе находят условные контурные токи, которые протекают в независимых контурах цепи. На втором этапе находят реальные токи в ветвях как алгебраическую сумму соответствующих контурных токов, протекающих в этих ветвях.

Дата добавления: 2015-05-06