Теорема о вложенных отрезках

Пусть имеется множество отрезков, таких, что из любых двух один содержит другой. Тогда все эти отрезки имеют по крайней мере одну общую точку. (Краткая формулировка: Система вложенных отрезков всегда имеет общую точку.)

Док-во:

8. Число Эйлера (“e”).

Пусть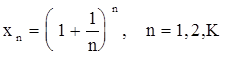

Покажем, что последовательность 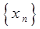сходится.

Раскрывая скобки согласно правилу бинома Ньютона, получим

+

= ...+

.

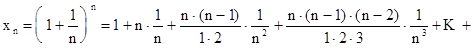
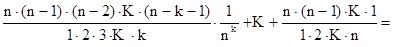
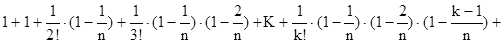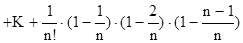При переходе от 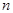к 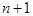число слагаемых, которые все положительны, возрастает, и кроме того, каждое слагаемое увеличивается:

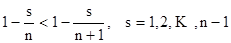, то .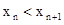

Далее, замечая, что каждая из скобок вида 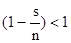и 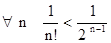, получим

.

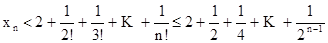В левой части неравенства - бесконечно убывающая геометрическая прогрессия .

Следовательно, .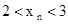

Но последовательность 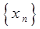монотонно возрастает и ограничена сверху, а значит, имеет предел, который обозначим буквой е.

Дата добавления: 2015-03-29