Геометрия владеет двумя сокровищами: одно из них — это теорема Пифагора, а другое — деление отрезка в среднем и крайнем отношении

Золотое сечение - гармоническая пропорция

О золотом сечении

Золотое сечение и вопросы теории композиции

Спор о том, должна или не должна наука
вторгаться в заповедные области искусства, идет
давно. И спор этот носит явно схоластический
характер. Во все эпохи процветания искусство
вступало в союз с наукой. Художники-мыслители,
теоретики и педагоги, размышлявшие над пробле-
мами обучения молодых, всегда приходили к вы-
воду, что без науки искусство развиваться и про-
цветать не может. Художник и педагог Н. П. Кры-
мов писал: «Говорят: искусство не наука, не
математика, что это творчество, настроение и что
в искусстве ничего нельзя объяснить — глядите и
любуйтесь. По-моему, это не так. Искусство объяс-
нимо и очень логично, о нем нужно и можно знать,
оно математично... Можно точно доказать, почему
картина хороша и почему плоха» ¹В. И. Суриков
утверждал, что в композиции есть какой-то непре-
ложный закон, когда в картине нельзя ничего ни
убрать, ни добавить, даже лишнюю точку поста-
вить нельзя, это настоящая математика.

Известный французский архитектор и теоретик
архитектуры XIX в. Виолле-ле-Дюк считал, что
форма, которую невозможно объяснить, никогда
не будет красивой. На дверях Сикионской школы
рисунка в Древней Греции было написано: «Сюда
не допускаются люди, не знающие геометрии». Не
следует художникам бояться математики, она
вовне и внутри нас. За кажущейся простотой и
случайностью живого восприятия окружающей дей-
ствительности скрывается математика. Когда мы
слушаем музыку, наш мозг занимается алгеброй.
Когда мы смотрим на что-либо, наш мозг занима-
ется геометрией. У человека не может возникнуть
отношение к предмету, чувство, эмоция, пока мозг

¹ Крымов Н. П.—художник и педагог.—М., I960.—С. 32.

И. Кеплер (1571—1630)

не произвел «измерение», сравнение этого предмета
с уже имеющимся в памяти чем-то подобным.
Впереди идет математика, а только потом возни-
кает чувство. Эту работу мозг производит мгновен-
но, потому мы ее не замечаем и не осознаем и нам
кажется, что чувство возникает сразу.

Прежде чем определить золотое сечение, необ-
ходимо ознакомиться с понятием пропорции.
В математике пропорция (лат. proportio) — это
равенство между двумя отношениями четырех ве-
личин: а: Ь = с: d. Далее, для примера обратимся
к отрезку прямой (рис. 1). Отрезок АВ можно
разделить на две равные части (/). Это будет
соотношение равных величин — АВ: АС = АВ: ВС.
Эту же прямую (2, 3) можно разделить на две
неравные части в любом отношении. Эти части
пропорции не образуют. Отношение малого отрезка
к большому или меньшего к большему есть, а со-
отношения (пропорции) нет. И, наконец, прямую
АВ(4) можно разделить по золотому сечению,
когда АВ: АС, как АС: ВС. Это и есть золотое
деление или деление в крайнем и среднем отно-
шении.

Из вышеизложенного следует вывод, что золо-
тое сечение — это такое пропорциональное гармо-
ническое деление отрезка на неравные части, при
котором весь отрезок так относится к большей
части, как сама большая часть относится к мень-
шей; или другими словами, меньший отрезок так
относится к большему, как больший ко всему,
т. е. a: b = b: с или с \Ь = Ь: а (рис. 2). Определе-
ние— деление в крайнем и среднем отношении —
становится более понятным, если мы выразим его
геометрически (рис. 3), а именно а: Ь как Ь: с.

Из рис. 3 понятно, почему астроном Иоганн
Кеплер называл золотую пропорцию продолжаю-
щей саму себя. «Устроена она так,— писал И. Кеп-
лер,— что два младших члена этой нескончаемой
пропорции в сумме дают третий член, а любые
два последних члена, если их сложить, дают сле-

РИС. I.

Деление отрезка прямой на равные части и по золотому се-
чению:

Рис. 2.

Геометрическое и алгебраическое выражение золотой пропор-
ции:
а: в =в:с или с: в =в: а

дующий член, причем та же пропорция сохраняет-
ся до бесконечности» ¹.

Как видим, построение ряда отрезков золотой
пропорции можно производить как в сторону уве-
личения (возрастающий ряд), так и в сторону
уменьшения (нисходящий ряд). В последнем слу-
чае необходимо от большего отрезка вычесть мень-
ший— получим еще меньший: b — a = d, и т. д.

Практическое знакомство с золотым сечением
обычно начинают с деления отрезка прямой в зо-
лотой пропорции геометрическим способом (рис.4).

I —АВ; АС=АВ: ВС (образуется пропорция); 2, 3 — пропорция не об-
разуется; 4—АВ:АС=АС:ВС или ВС: АС=АС: АВ (золотая пропор-
ция)

¹ Кеплер И. О шестиугольных снежинках.—М., 1982.—
С. 17.

Рис. 3.

Среднее пропорциональное или деление отрезка в крайнем и среднем отношении:

й — Ь — а; с=а+Ь

Рис. 4. Рис. 5.

Геометрическое деление отрезка прямой по золотому сечению Определение линии золотого сечения на картине геометриче-
(разработано А. Дюрером): ским способом:

ВС =0,5 АВ; CD =ВС ВС =0,5 АВ

Рис. 6.

Применение золотого сечения в построении картины И. Е. Репина «А. С. Пушкин на акте в Лицее 8 января 1815 года»

Из точки В восставляется перпендикуляр, равный
половине АВ. Полученная точка С соединяется
линией с точкой А. На полученной линии отклады-
вается отрезок ВС, заканчивающийся точкой D.
Отрезок AD переносится на прямую АВ. Получен-
ная при этом точка £ делит отрезок АВ в соот-
ношении золотой пропорции. Арифметически отрез-

ки золотой пропорции выражаются бесконечной
иррациональной дробью. АЕ = 0,618..., если АВ
принять за единицу, ££ = 0,382.... В практике при-
меняется округление: 0,62 и 0,38. Если отрезок АВ
принять за 100 частей, то большая часть отрезка
равна 62, а меньшая — 38 частям.

При переносе геометрического способа деления

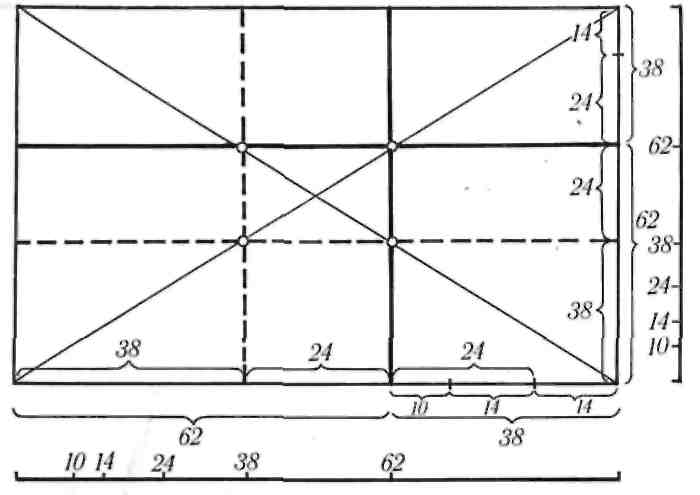
Рис. 7.
Линии золотого сечения и диагонали на картине

на картину или эскиз поступают так: половину
длины картины или эскиза откладывают на высоту
или продолжение высоты, если эскиз узкого фор-
мата. Полученную точку С соединяют с левым
нижним углом картины и т. д. (рис. 5). Линия
золотого сечения в левой части картины будет
находиться на таком же расстоянии от левого края,
как и в правой от правого (показано пунктиром).
Указанные выше две пропорции золотого деле-
ния — равные величины и неравные, при этом про-
порциональные, широко используются в искусстве.

Фигура А. С. Пушкина в картине И. Е. Репина
«А. С. Пушкин на акте в Лицее 8 января 1815 г.»
помещена художником на линии золотого сечения
в правой части картины (рис. 6). Левая часть
картины, в свою очередь, тоже разделена в про-
порции золотого сечения: от головы А. С. Пушкина
до головы Г. Р. Державина и от нее до левого
края картины. Расстояние от головы Державина
до правого края картины разделено на две равные
части линией золотого сечения. В нижней части
картины глаз улавливает деление на три равные
части. Их образуют стол в левой части картины,
нога Пушкина правее линии золотого сечения и
правый край картины.

Если необходимо найти линию золотого сече-
ния на картине или эскизе по горизонтали, то
новое деление геометрическим способом высоты
картины производить нет необходимости. Доста-
точно провести диагонали картины. Их пересече-

ния с линиями золотого сечения по вертикали
укажут точки, через которые следует провести
горизонтальные линии золотого сечения (рис. 7).
Эти линии могут понадобиться при построении пей-
зажа. Художники-пейзажисты из опыта знают, что
нельзя отводить половину плоскости холста под
небо или под землю и воду. Лучше брать или
больше неба, или больше земли, тогда пейзаж
«лучше смотрится».

Из пропорции золотого сечения вытекает, что
если высоту или ширину картины разделить на
100 частей, то больший отрезок золотой пропорции
равен 62, а меньший — 38 частям. Эти три вели-
чины позволяют нам построить нисходящий ряд
отрезков золотой пропорции: 100 — 62 = 38; 62 —
— 38 = 24; 38 — 24=14; 24— 14=10.

100, 62, 38, 24, 14, 10 — это ряд величин золотой
пропорции, выраженных арифметически. Так же
находят отрезки золотой пропорции и на картине,
если линия золотого сечения по вертикали уже
проведена (рис. 7). Переносим линию золотого
сечения в левый край картины. Расстояние между
линиями золотого сечения в середине картины рав-
но 24 частям. Отрезок, равный 24 частям, отклады-
ваем на отрезок, равный 38 частям, и получаем
остаток, равный 14 частям. Последний отрезок
накладываем на отрезок, равный 24 частям, и по-
лучаем отрезок, равный 10 частям. Все отрезки
нисходящего ряда золотой пропорции для данной
картины мы получили. Ту же операцию проводим
и с высотой картины. Полученные отрезки пере-
носим на полоску плотной бумаги или картона —
для ширины с лицевой стороны и для высоты с
оборотной. Этот простейший инструмент назовем
пропорциональной линейкой. Такая пропорцио-
нальная линейка пригодна только для данного
эскиза или эскиза такого же размера. Изготовле-
ние ее занимает несколько минут, но в дальнейшем
облегчит работу над эскизом в поисках интервалов
между фигурами или группами фигур, между
предметами, поможет найти их размеры и, в ко-
нечном итоге, гармонизовать линейное построение
картины.

Фигура А. С. Пушкина в картине Н. Н. Ге
«Александр Сергеевич Пушкин в селе Михайлов-
ском» поставлена художником на линии золотого
сечения в левой части полотна (рис. 8). Ыо и все
остальные величины по ширине вовсе не случайны:
ширина печи равна 24 частям от ширины картины,
этажерки— 14 частям, расстояние от этажерки до

Рис. 8.

Пропорции золотого деления в линейном построении картины Н. Н. Ге «Александр Сергеевич Пушкин в селе Михайловском

печи также равно 14 частям и т. д. Такие же
величины есть и в картине И. Е. Репина (см. рис. 6):
от левого края картины до головы Державина —
24 части; от стола до носка сапога правой ноги
Пушкина — 24 части. Такое же расстояние от го-
ловы Пушкина до головы военного, с восторгом
слушающего чтение поэта (его голова находится
на второй линии золотого сечения в таком же

повороте, как и голова Пушкина). От голов
Пушкина до головы молодой женщины в право
части картины, с умилением слушающей деклама-
цию, тоже — 24 части, а от ее головы до npaвого
края картины — 10 частей и т. д.

Повторение равных величин, чередование paв-
них и неравных величин в пропорциях золотое
сечения создает в картине определенный ритмиче-

Рис. 9.

Ряд отрезков золотой пропорции

скии строй, вызывающий у зрителя то или иное
настроение и втягивающий его в рассматривание
изображения. Порядок и последовательность этого
рассматривания предопределены художником.

Достоинство пропорции золотого сечения за-
ключено в том, что, раз поделив отрезок прямой
или сторону картины геометрическим способом,
получают отрезки любого уменьшения. В практи-
ческой же работе художника достаточно величин,
соответствующих числовым значениям 62, 38, 24,
14 и 10 (рис. 9).

Отрезки золотой пропорции нисходящего ряда
при известной величине отрезка АВ или ширине
эскиза, картины, репродукции — если мы желаем
их проанализировать, получают путем вычисления.
Например, ширина эскиза равна 14 см. Одна сотая
часть от 14 составит 0,14 см. 0,14 умножаем на
62 и получаем больший отрезок золотой пропорции,
равный 8,68 см. Следовательно, 100 частей = 14,00;
62 части = 8,68; 38 частей = 5,32; 24 части = 3,36;
14 частей = 1,96; 10 частей = 1,4 см.

Откладываем эти значения на пропорциональ-
ной линейке, как показано на рис. 7, и дальнейшую
работу над эскизом проводим с помощью этой
линейки. Интуитивное сочетается с математикой
и расчетом.

Случается так, что размер эскиза равен 10 см
(100 мм) по ширине и высоте (квадрат). Тогда
золотая пропорция на эскизе или пропорциональ-
ной линейке откладывается по линейке: 62, 38 и
24 мм. При размере картины 100x100 см посту-
пают аналогичным образом. Если же одна из сто-
рон картины равна 100 см, то, отложив на ней
с помощью линейки отрезки золотой пропорции,
проводим линии золотого сечения. Пересекаем их

диагоналями и получаем данные для нахождения
отрезков золотого сечения для другой стороны
картины, не равной 100 см, как показано на рис. 7.
Когда эскиз не очень большой, применяют ме-
тод нахождения золотых пропорций на одной из
его сторон при помощи проведения вспомогатель-
ной линии размером в 10 см (100 мм) под произ-
вольным углом к разделяемой линии (рис. 10).
На вспомогательной линии, которую проводят в
плоскости эскиза или за его пределами, отклады-

Рис. 10.

Вспомогательная линия длиной в 100 мм (10 см) для нахожде-
ния отрезков золотой пропорции на эскизе малого размера

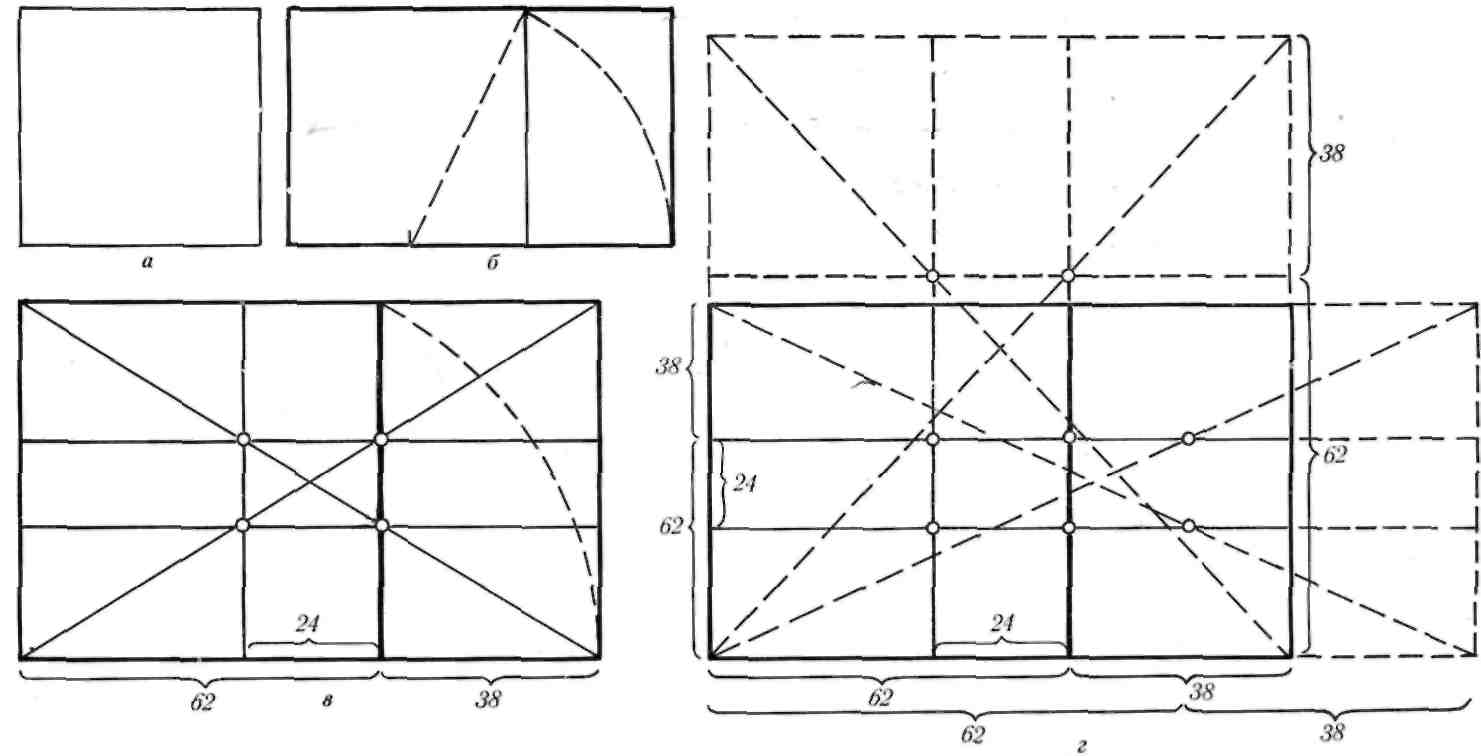
Рис. 11.

Способы нахождения отрезков золотой пропорции по методу «от квадрата»:
а —квадрат; б — прямоугольник золотого сечения; в — получение точек для проведения линий золотого сечения по горизонтали; г — построение

эскиза любого формата

вают значения в миллиметрах — 62, 38, 24, 14 и 10.
Крайняя точка вспомогательной линии соединяется
с краем эскиза. Остальные линии проводятся па-
раллельно первой. Все остальное построение про-
водится, как показано на рис. 7. Этот метод пред-
ложен художником В. Скубаком. Этот же метод
применяют и на небольшой картине, когда вспо-
могательная линия в 100 см располагается на ее
поверхности.

Если размер эскиза не задан, его построение
начинают с квадрата (рис. 11, а). Разделив ниж-
нюю сторону квадрата на две равные части и про-
ведя линию от полученной точки в правый верхний
угол квадрата, принимаем эту линию за радиус
и описываем дугу до пересечения с продолжением
нижней стороны квадрата. Из полученной точки
восставляем перпендикуляр до пересечения его с
продолжением верхней стороны квадрата. В ре-
зультате такого построения получаем прямоуголь-

ник золотого сечения, или золотой прямоугольник

(рис. 11, б). Если ширину такого прямоугольника
принять за 100 частей, то его высота равна 62 ча-
стям. Линия золотого сечения по вертикали опре-
делится сама собой. Далее проводим диагонали,
получаем точки для проведения линий золотого
сечения по горизонталям (рис. 11, в). На основа-
нии золотого прямоугольника производят построе-
ние эскиза любого формата, вытянутого по гори-
зонтали или вертикали (рис. 11, г).

В русской Академии художеств знали о законе
золотого сечения. Этому есть письменные свиде-
тельства. В книге «Далекое — близкое» И. Е. Ре-
пин описывает встречу знаменитого критика
В. В. Стасова с учениками Академии художеств.
На встрече присутствовали, кроме Репина и Ста-
сова, М. М. Антокольский, Г. И. Семирадский,
К. А. Савицкий и др. Разговор шел о новом реали-
стическом искусстве и устаревшем академизме.

Илья Ефимович отмечает, что Семирадский ще-
голял перед Стасовым знанием греческого искус-
ства, эстетических трактатов и золотого сечения,
и замечает, что все это прекрасно знал и В. В. Ста-
сов.

Золотое сечение применялось художниками при
композиционном построении картин. Был разрабо-
тан упрощенный метод, когда плоскость картины
делилась на 10 частей по вертикали и горизонта-
ли. Линия золотого сечения намечалась в отноше-
нии 6 и 4 частей (рис. 12, а). Это не давало
отношения 62:38, но давало близкое к нему
60:40. Практически этого было достаточно, чтобы
ориентироваться и расположить главную фигуру
или группу фигур в наиболее выгодном для этого
месте картины.

Академик А. Н. Лаптев в статье «Некоторые
вопросы композиции» так пишет о золотом сече-
нии: «...Хочу упомянуть о давно известном, особен-
но в классическом искусстве, законе пропорций
золотого сечения. В силу некоторого свойства
нашего зрительного восприятия, эти пропорции
(примерно 6 и 4) являются наиболее гармониче-
скими и наиболее отвечающими общему понятию
красоты, а потому и наиболее часто употребляе-
мыми» ¹.

Тот же результат получали и художники Мюн-
хенской академии делением картины на 5 частей.
Золотая пропорция бралась в отношении 3: 2, что
одно и то же, так как сокращение 10; 6 и 4 в два
раза дает 5; 3 и 2. Главная фигура картины или
группа помещались на линии золотого сечения
(рис. 12,б).

В картине Джованни Тьеполо «Пир Клеопат-
ры» голова Клеопатры помещена художником в
правой верхней точке на пересечении линий золо-
того деления по вертикали и горизонтали. Этим
обеспечивается легчайшее восприятие глазом всей
картины и ее зрительно-смыслового центра —
центра внимания. Центр внимания может быть в
правой части картины или в левой, в нижней или
верхней. Эти четыре точки — наилучшие места для
расположения главного предмета картины. Это
связано "с устройством глаза, работой мозга и
закономерностями зрительного восприятия, о чем
будет сказано ниже.

На одном из эскизов В. И. Сурикова к картине

Рис. 12.

Деление картины:

а — на 10 частей в Русской Академии художеств: б — на пять частей
в Мюнхенской академии художеств

«Боярыня Морозова» хорошо видны деления пра-
вого вертикального края эскиза на 10 частей.
Затем отсчитаны 6 делений снизу или 4 сверху
и проведена линия золотого сечения, являющаяся
предполагаемым горизонтом. Репродукция этого
эскиза опубликована в книге С. Каплановой «От
замысла и натуры к законченному произведению» ².
В ранней картине В. И. Сурикова «Милосерд-
ный самарянин» (1874) голова раненого помещена
художником в правой нижней точке картины,
ладонь правой руки самарянина — в левой верх-
ней, где слуга льет в нее воду из кувшина. Обе
эти точки находятся на диагонали. Устойчивость

¹ Лаптев А. М. Некоторые вопросы композиции//Вопросы ² Капланова С. От замысла и натуры к законченному

изобразительного искусства.— М, 1954.—С. 66—67. произведению.—М., 1981.—С. 17.

Рис. 13.

Диагонали, линии золотого сечения и смысловой центр картины В. И. Сурикова «Милосердный самарянин»

композиции придает и то, что голова самарянина
находится на средней линии картины по вертикали
(рис. 13).

Недостаток деления картины на 10 или 5 ча-
стей заключен в том, что оно дает довольно при-
близительные отрезки золотого сечения — 60, 40,
20 (табл. 1, ряд 1). Более точные значения про-
порциональных величин золотого сечения (62 и
38) дают возможность образовать 5 величин золо-
того ряда (табл. 1, ряд 2), еще более точные
исходные величины —61,8; 38,2 или 61,803 и 38,196
дают возможность продолжить нахождение вели-

чин нисходящего ряда золотой пропорции до 9 зна-
чений или даже до бесконечности (табл. 1, ряды
3 и 4). В практической работе художника над
эскизом или картиной достаточно величин 2-го и
3-го рядов.

Формат картины или монументальной росписи
иногда задают. Но чаще всего художник сам
определяет формат в соответствии со своим замыс-
лом. Например, художник начинает разрабатывать
эскиз пейзажа форматом 8x12 см. Эскиз имеет
формат 8X12 см. Для нахождения линии золотого
сечения по вертикали и отрезков золотого сечения

Рис. 14.

Дата добавления: 2015-05-06