Золотое сечение и симметрия

Ряд

Построение пейзажа по золотому сечению и нахождение от- резков золотой пропорции при помощи вспомогательной линии

по нисходящему ряду можно воспользоваться про-
ведением вспомогательной линии длиной 10 см за
пределами поля эскиза (рис. 14). На основании
наблюдений, зарисовок, этюдов у автора возник
замысел: показать на картине опушку леса. Вни-
мание зрителя в первую очередь привлекает ель.
Все остальные деревья дополняют пейзаж и обра-
зуют стройное гармоническое целое, легко воспри-
нимаемое глазом. Такое гармоническое целое
создается благодаря расположению ели на линии
золотого сечения, а остальных деревьев или групп
деревьев — в должном порядке. Подсказывают этот
порядок (ритм) отрезки нисходящего ряда золо-
того сечения для данной картины, найденные при
помощи вспомогательной линии и отложенные на
пропорциональной линейке (для ширины и высо-
ты). Дальнейшая работа над пейзажем пойдет «на
глаз», по чувству. Пусть художественный вкус
автора, опыт и талант поведут его к успешному
завершению картины, к наилучшему выражению
замысла. Как в архитектуре, так и в живописи
геометрию привлекают для нужд пропорциониро-
вания, для создания предварительной схемы, ком-
позиционного каркаса, но не более.

Таблица 1. величины нисходящего ряда золотой пропорции

1-й	2-й	3-й	4-й
		61,8	61,803
		38,2	38,196
		23,6	23,606
		14,5	14,589
		9,0	9,017
		5,5	5,572
		3,5	3,444
		2,0	2,128
		1.5	1,315 0,813 0,502 0,311 и т. д.

Для нахождения отрезков золотой пропорции
восходящего и нисходящего рядов можно пользо-
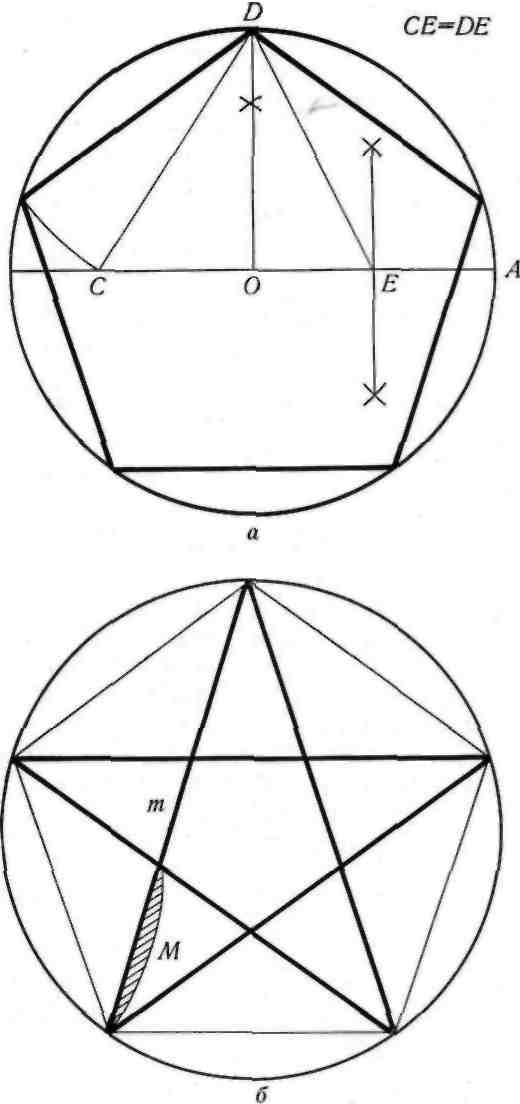
ваться пентаграммой (рис. 15). Для построения
пентаграммы необходимо построить правильный
пятиугольник. Способ его построения разработал
немецкий живописец и график Альбрехт Дюрер
(1471 — 1528) (рис. 15, а). Пусть О — центр окруж-
ности, А — точка на окружности и Е — середина
отрезка ОА. Перпендикуляр к радиусу ОА, вос-
ставленный в точке О, пересекается с окружностью
в точке D. Пользуясь циркулем, отложим на диа-
метре отрезок CE = ED. Длина стороны вписанного
в окружность правильного пятиугольника рав-
на DC. Откладываем на окружности отрезки DC
и получаем пять точек для начертания правильного
пятиугольника. Соединяем углы пятиугольника
через один диагоналями и получаем пентаграмму
(рис. 15, б). Все диагонали пятиугольника делят
друг друга на отрезки, связанные между собой
золотой пропорцией. Проводим прямую произволь-
ной длины, откладываем на ней отрезок m, ниже
откладываем отрезок М. На основании этих двух
отрезков выстраиваем шкалу отрезков золотой
пропорции восходящего и нисходящего рядов
(рис. 15, в).

Если размер эскиза не задан, берут любые два
значения шкалы как ширину или высоту эскиза
и находят все остальные величины, как было пока-
зано ранее.

Из всего сказанного вытекает, что художник,
желающий осуществить гармонический пропорцио-

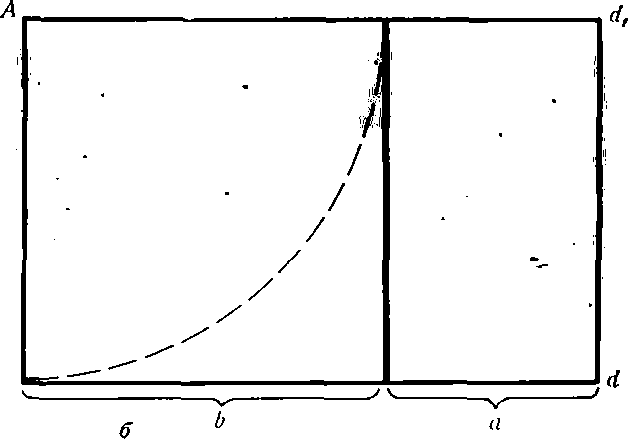
Рис. 16. Построение: а —золотого треугольника: а:в =Ф, в=dd₁ ; б — золотого прямоугольника: а: в = Ф

Рис. 15.

Построение правильного пятиугольника (а), пентаграммы (б)
и шкалы отрезков (в) золотой пропорции

нальный строй своей картины на основании золо-
того сечения, обязательно находит первые два
отрезка золотой пропорции. Решению этой задачи
способствует и золотой треугольник. Каждый конец
пятиугольной звезды представляет собой золотой

треугольник. Его стороны образуют угол 36° при
вершине, а основание, отложенное на боковую сто-
рону, делит ее в пропорции золотого сечения. Для
построения золотого треугольника' не требуется
даже транспортир (рис. 16, а). Проводим пря-
мую АВ. От точки А откладываем на ней три раза
отрезок О произвольной величины, через получен-
ную точку Р проводим перпендикуляр к линии АВ,

на перпендикуляре вправо И влево От точки Р
откладываем отрезки О. Полученные точки d и d\
соединяем прямыми с точкой А. Отрезок dd\ откла-
дываем на линию Ad\, получая точку С. Она раз-
делила линию Ad₁ в пропорции золотого сечения.
Линиями Ad\ и dd\ пользуются для построения золо-
того прямоугольника (рис. 16, б).

Золотое сечение нельзя рассматривать само по
себе, отдельно, без связи с симметрией. Великий
русский кристаллограф Г. В. Вульф (1863—1925)
считал золотое сечение одним из проявлений сим-
метрии.

Золотое деление не есть проявление асиммет-
рии, чего-то противоположного симметрии. Соглас-
но современным представлениям золотое деле-
ние— это асимметричная симметрия. Сейчас в
науку о симметрии вошли такие понятия, как
статическая и динамическая симметрия. Статиче-
ская симметрия характеризует покой, равновесие,
а динамическая — движение, рост. Так, в природе
статическая симметрия представлена строением
кристаллов, а в искусстве характеризует покой,
равновесие и даже застылость. Динамическая сим-
метрия выражает активность, характеризует дви-
жение, развитие, ритм, она — свидетельство жизни.
Симметрии свойственны равные отрезки, равные
величины. Динамической симметрии свойственно
увеличение отрезков (или их уменьшение), и оно
выражается в величинах золотого сечения возра-
стающего или убывающего ряда.

Художественная форма, в основе построения
которой лежат пропорции золотого сечения, и осо-
бенно сочетание симметрии и золотого сечения,
является высокоорганизованной формой, способ-
ствующей наиболее ясному выражению содержа-
ния, наилегчайшему зрительному восприятию и
появлению у зрителя ощущения красоты.

Очень часто в одном и том же произведении
живописи встречается сочетание симметричного
деления на равные части по вертикали и деление
на неравные части по золотому сечению по гори-
зонталям.

Картина Леонардо да Винчи «Мадонна в гроте»
не строго симметрична, но в основе ее построе-
ния— симметрия (рис. 17, а). Все содержание
картины выражается в фигурах, которые размести-
лись в нижней ее части. Они вписываются в квад-

рат. Но художник не довольствовался таким фор-
матом. Он достраивает над квадратом прямоуголь-
ник золотого сечения (рис. 17, б). В результате
такого построения вся картина получила формат
золотого прямоугольника, поставленного верти-
кально. Радиусом, равным половине стороны квад-
рата, он описал окружность и получил полукружие
верхней части картины. Внизу дуга пересекла ось
симметрии иуказала размер еще одного прямо-
угольника золотого сечения в нижней части карти-
ны (рис. 17, в). Затем радиусом, равным стороне
квадрата, описывается новая дуга, которая дала
точки на вертикальных сторонах картины. Эти
точки помогли построить равносторонний треуголь-
ник, который и явился каркасом для построения
всей группы фигур. Все пропорции в картине яви-
лись производными от высоты картины. Они обра-
зуют ряд отношений золотого сечения и служат
основой гармонии форм и ритма, несущих в себе
скрытый заряд эмоционального воздействия. Ана-
логичным образом построена картина Рафаэля
«Обручение Марии» (рис. 18).

Если мы обратимся к древнерусской живописи,
иконам XV—XVI вв., то увидим такие же приемы
построения изображения. Иконы вертикального
формата симметричны по вертикали, а членения по
горизонталям осуществлены по золотому сечению.
Икона «Сошествие во ад» Дионисия и мастерской
(рис. 19) с математической точностью рассчитана
в пропорциях золотого сечения.

В иконе конца XV в. «Чудо о Флоре и Лавре»
осуществлено тройное отношение золотого сечения.
Сначала мастер разделил высоту иконы на две
равные части. Верхнюю отвел под изображение
ангела и святых. Нижнюю часть он разделил на
два неравных отрезка в отношении 3: 2. В итоге
получилось соотношение трех величин золотого се-
чения: а: Ь, как b: с. В числах это будет выглядеть
так: 100, 62, 38, а уменьшенные вдвое — 50, 31, 19.

О симметричности «Троицы» Андрея Рублева
написано много. Но никто не обратил внимания
на то, что по горизонталям и здесь осуществлен
принцип золотых пропорций (рис. 20). Высота
среднего ангела относится к высоте боковых анге-
лов, как их высота относится к высоте всей иконы.
Линия золотого сечения пересекает ось симметрии
по середине стола и чаши с жертвенным тельцем.
Это — композиционный замок иконы. На рисунке
показаны и более мелкие величины ряда золотого
сечения. Наряду с плавностью линий, колоритом

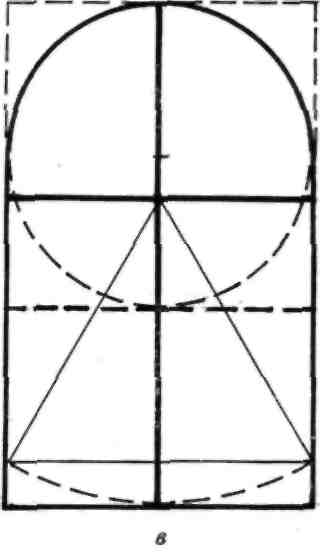
Рис. 17.

Использование симметрии и
золотого сечения в картине
Леонардо да Винчи «Мадон-
на в гроте»:
а — пропорции золотого сечения:
б — размещение персонажей

картины в квадрате; в — схема
линейного построения картины

Рис. 18.

Использование симме-
трии и золотого сече-
ния в картине Рафа-
эля «Обручение Ма-
рии

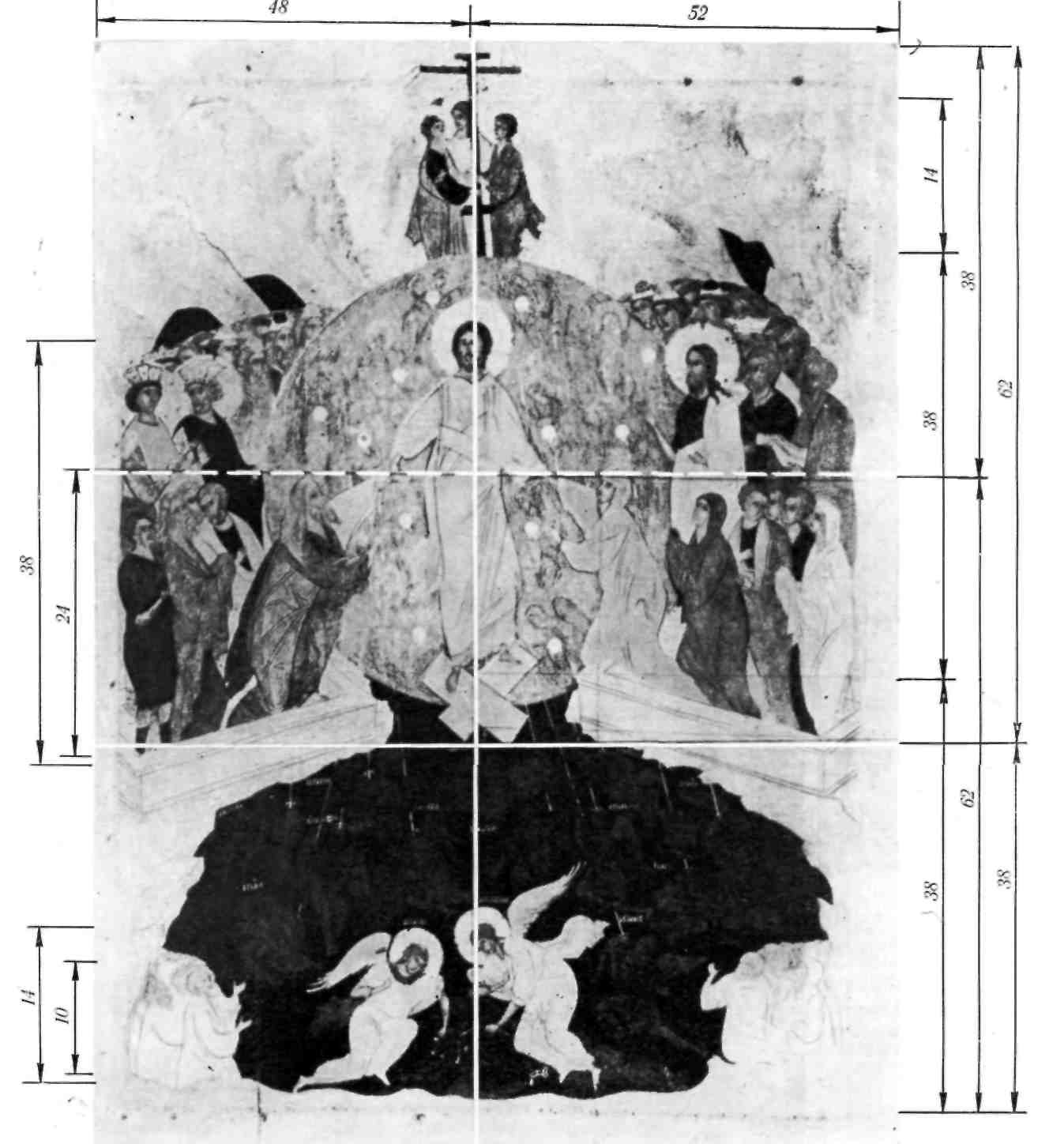
Рис. 19.

Золотые пропорции в линейном построении изображения на иконе «Сошествие в ад» Дионисия и мастерской (XVI в.)

Рис. 20.

Симметрия и золотые пропорции в линейном построении «Троицы» Андрея Рублева

Золотое сечение

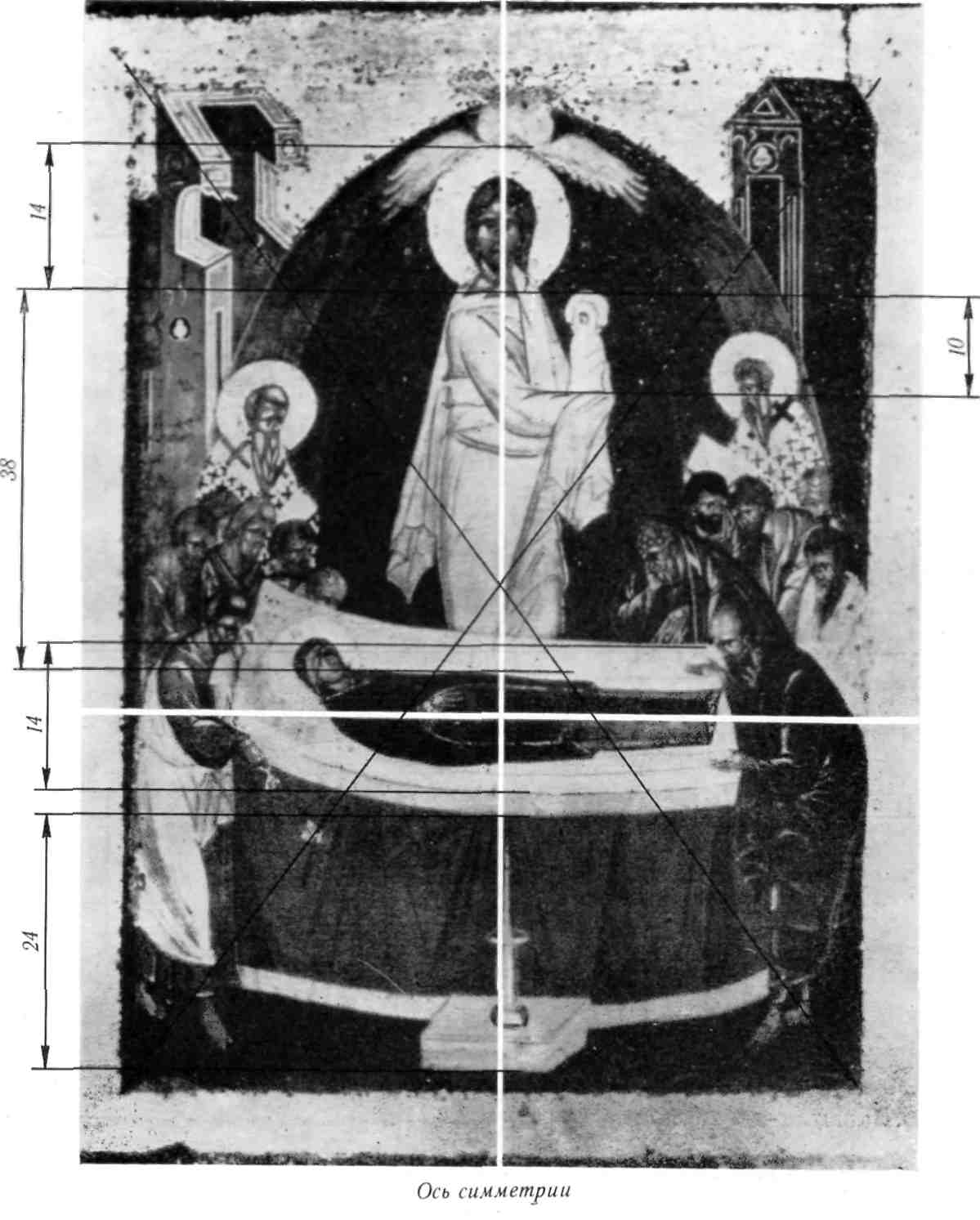
Рис. 21. Симметрия и золотые пропорции в линейном изображении «Успения» Феофана Грека

Рис. 22.

Золотые пропорции в линейном построении изображения на плите фараона Нармера (3-е тыс. до н. э.)

пропорции иконы играют значительную роль в
создании того общего впечатления, которое испы-
тывает зритель при ее рассматривании.

Могучим хоралом представляется нашему взору
икона Феофана Грека «Успение» (рис. 21). Сим-
метрия и золотое сечение в построении придают
этой иконе такую мощь и стройность, какую мы
видим и ощущаем при виде греческих храмов и
слушании фуг Баха. Легко заметить, что компози-
ция «Успения» Феофана Грека и «Троицы» Андрея
Рублева одна и та же. Исследователи творчества
древнерусских художников отмечают, что заслуга
Феофана Грека состоит не столько в том, что он
писал фрески и иконы для русских соборов и церк-
вей, сколько в том, что он научил античной муд-
рости Андрея Рублева.

Завершим хвалу содружеству симметрии и

золотого сечения рассмотрением пропорций побед-
ной плиты египетского фараона Нармера (3-е тыс.
до н. э.). Прямоугольник золотого сечения — исход-
ная форма плиты Нармера (рис. 22). Плита
разбита на пояски, высота которых выдержана в
пропорциях золотого сечения. Высота фигуры фа-
раона— от верхнего пояска до нижнего — равна
62 частям высоты. Нижняя часть плиты от пояска
до края равна 24 частям, а верхняя, от верхнего
пояска до верхнего края,— 14 частям. Ритмический
строй оборотной стороны плиты несколько иной,
потому что содержание изображения потребовало
иного сопоставления пропорциональных величин.
Пропорции золотого сечения и симметрия дают
бесконечное разнообразие композиционных по-
строений как в самой природе, так и в произведе-
ниях искусства всех родов и видов.

Дата добавления: 2015-05-06