Методы вероятностной (случайной) выборки

Вероятностная (случайная) выборка (Probability Samplinq) – метод формирования выборки предполагающий, что вероятность попадания в выборку каждого элемента совокупности известна и больше нуля.

Вероятностные методы включают:

- простой случайный отбор,

- систематический отбор,

- кластерный отбор,

- стратифицированный отбор.

Простой случайный отбор предполагает, что вероятность быть избранным в выборку известна и является одинаковой для всех единиц совокупности. Вероятность быть включенным в выборку определяется отношением объема выборки к размеру совокупности.

Простой случайный отбор может осуществляться с помощью следующих методов: формирование выборки вслепую и с помощью таблицы случайных чисел.

При использовании метода формирование выборки вслепую единицы совокупности в соответствием с их фамилиями, названиями или другими признаками вносятся в карточки, которые в перемешанном виде помещаются в какую-то непрозрачную емкость (ящик, коробку и т.п.). Из данной емкости кто-то случайным образом вытягивает число карточек, определяемое объемом выборки.

В таблицах случайных чисел содержатся числа, порядок включения которых в таблицу осуществлен случайным образом. Единицам совокупности присваивают порядковые номера. В таблице случайных чисел выбирается любая начальная точка и, двигаясь в произвольном направлении и произвольно меняя направление движения, выбирается необходимое количество номеров из числа присвоенных, равное заранее установленному объему выборки.

Кроме того, используются генераторы случайных чисел. Например, при телефонном интервьюировании компьютер, имеющий генератор случайных чисел, может генерировать случайным образом телефонные номера.

Начальная часть метода систематического отбора соответствует начальной части метода простого случайного отбора: необходимо получить полный список единиц генеральной совокупности.

Однако далее вместо присвоения порядковых номеров используется показатель "интервал скачка", рассчитанный как отношение размера совокупности к объему выборки. Например, если используется телефонный справочник и интервал скачка был определен равным 250, то это означает, что каждый 250-й телефонный номер включается в выборку. Однако для определения начальных страницы и колонки справочника используются случайные числа.

Особенно широко метод систематического отбора используется, когда для различных видов совокупностей имеются различные справочники, списки, спецификации и т.п. материалы.

Другим методом вероятностного отбора является кластерный отбор, основанный на делении совокупности на подгруппы, каждая из которых представляет совокупность в целом. Базовая концепция данного метода очень похожа на базовую концепцию метода систематического отбора, однако реализация этой концепции осуществляется по-другому. Предположим, что исследуется мнение населения какого-то региона относительно марки какого-то товара.

Регион разбивается на четко определяемые части (кластеры), например, области. Исследователь может считать, что выделенные кластеры являются идентичными, и мнение населения этих областей характерно для региона в целом. Далее одна из областей (один кластер) выбирается случайным образом, определяется совокупность для этой области, в ней проводится соответствующее исследование, а выводы обобщаются на совокупность всего региона (одноступенчатый подход).

Примером квази-случайного отбора является механическая выборка. Проведение механической выборки требует списка характеристик респондентов (фамилии, адреса, телефоны и т.д.). Из этого списка через равные промежутки люди отбираются в выборку. Этот промежуток называется шагом выборки - К.

К = N/n (округляется отбрасыванием дробной части),

где N - объем генеральной совокупности; n - объем выборочной совокупности.

Начало отбора выбирается случайным образом в пределах шага выборки. Например, если шаг выборки равен 20, то начинать отбор надо с любого числа от 1 до 20.

При определении ошибки репрезентативности и объема выборки используются те же формулы, что и при случайной выборке. Процедура проведения механической выборки менее громоздка, чем проведение случайной выборки. Механическая выборка может быть как более точной, так и менее точной по сравнению со случайной выборкой.

В основе всех описанных методов лежит предположение, что любая совокупность характеризуется симметричным распределением ее ключевых характеристик. Говоря другими словами, каждая выборка достаточно полно характеризует всю совокупность, различные крайности в выборке уравновешивают друг друга. Такая ситуация на практике встречается крайне редко. Скажем, исследуется рыночный потенциал определенного региона для какого-то товара. Население больших, средних и малых городов, сельской местности данного региона отличается по уровню образования, доходу, образу жизни и т.п.

В случае несимметричного распределения совокупности последняя разделяется на различные подгруппы (страты), например, по уровню доходов, и выборки формируются из этих подгрупп, по сути дела являющихся сегментами рынка. Тогда для обеспечения однородности данных прибегают к стратифицированной (районированной) выборке. Генеральную совокупность при этом разделяют на отдельные страты, более или менее однородные по составу, а затем из каждой страты производится расчет простой случайной (систематической) выборки. Такой метод носит название стратифицированного отбора.

Далее для каждой страты с помощью случайного отбора формируется выборка.

Например, при использовании лотерейного метода (метода жребия) жетоны с номерами всех элементов помещают в урну, тщательно перемешивают и извлекают последовательно п жетонов, где п - число элементов выборочной совокупности. Элементы генеральной совокупности, имеющие номера, оказавшиеся на извлеченных жетонах, составят выборочную совокупность. Это довольно продолжительная (при больших размерах выборки) операция, к тому же достаточно трудоемкая, поскольку для обеспечения равного шанса выбора необходимо тщательно перемешивать жетоны после каждой выемки очередного номера. При формировании равновероятностной выборки из больших совокупностей пользуются также таблицами случайных чисел. Часть такой таблицы случайных чисел показана в табл. 4.1.

Таблица 4.1

Фрагмент таблицы случайных чисел

Номер столбца   Номер строки

Пусть существует, скажем, популяция (генеральная совокупность) из 1507 элементов, и нужно спроектировать выборку численностью 150 элементов. При этом можно выбирать любые два смежных столбца в таблице случайных чисел: цифры, стоящие в двух смежных ячейках, будут образовывать четырехзначное число. Каждый раз при появлении числа от 0001 до 1507 будем считать, что оно обозначает номер отбираемого элемента. Когда число появляется более одного раза, этот номер игнорируется после первого раза. Если мы начнем с первых четырех столбцов спускаться по столбцам, то в выборку попадут элементы под номерами 0799, 1016, 0084, 480, 1306, 929, 1320 и 938. Поскольку мы не стремимся умышленно отыскать определенное число, можно начать с любого места таблицы и использовать любую систему для движения по таблице. С тем же успехом случайные числа могут генерироваться специальной программой компьютера.

Пример использования метода механической выборки, когда из пронумерованного списка через равные интервалы к отбирается заданное число респондентов. Предположим, что следует спроектировать выборку численностью 100 из списка 5000 студентов какого-то вуза. Если мы намерены использовать систематическую выборку, то должны вначале рассчитать интервал выборки делением числа элементов в списке на размер выборки. В данном случае, разделив общую численность студентов (5000) на размер выборки (100 единиц), мы получим интервал (шаг) выборки (50). Так что мы будем систематически двигаться по списку и отбирать каждого пятидесятого студента (отобрав, таким образом, 100 имен). Определение места в списке, с которого мы начнем, производится случайным образом, по таблице случайных чисел (случайный старт). Таким образом, если случайно выбрана точка старта под номером 31, в выборку попадут студенты под номерами 31,81,131,181 и т.д.

Несмотря на преимущества, систематическая выборка может иногда превратиться в предубежденную выборку, например, если элементы размещены в списке, ранжированном по каким-то характеристикам. При этом определение места начала случайного отбора влияет на средние характеристики всей выборки. Например, если фамилии студентов расставлены в списке не по алфавиту, а в соответствии со средним оценочным баллом - от высшего к низшему, то систематическая выборка из студентов, стоящих в списке под номерами 1,51,101, будет характеризоваться более низким средним баллом, чем выборка, включающая студентов под номерами 50,100 и 150. Каждая новая выборка будет давать новый средний балл, т.е. это и будет предубежденная выборка.

4.3. Методы невероятностной выборки

Невероятностная (неслучайная) выборка - способ отбора единиц выборочной совокупности, принцип которого отличен от случайного. Как и в случае с вероятностным отбором, основная цель неслучайного отбора состоит в получении совокупности, репрезентирующей изучаемый объект. Однако в отличие от вероятностной выборки статистические выводы обо всем множестве объектов в этом случае делать не вполне правомерно. Эти выводы так или иначе верны лишь для генеральной совокупности, которая не всегда совпадает с объектом исследования. Выделяют два основных вида неслучайной выборки (отбора): направленный (целенаправленный, целевой выбор по усмотрению) и стихийный.

При применении невероятностных методов отбора формирование выборки осуществляется без использования понятий теории вероятностей, вследствие чего невозможно рассчитать вероятность включения в выборку единицы совокупности.

Выделяют два основных вида невероятностного обора или неслучайной выборки:

- направленный (целенаправленный, целевой, выбор по усмотрению);

- стихийный.

Формами невероятностного или направленного отбора выступают: метод типичных представителей, квотная выборка, гнездовая выборка и метод «снежного кома».

Метод типовых представителей (типовая выборка) (judqemental Samplinq) – метод детерминированной выборки, при котором «эксперт», стремясь обеспечить репрезентативность опирается на свои собственные суждения.

Типовая выборка основана скорее на индивидуальной оценке исследователя, чем на случайном отборе элементов выборки. Исследователь может произвольно или сознательно решать, какие элементы включать в выборку. В результате проведения типовой выборки можно получить детальную оценку характеристик совокупности. Однако этот метод не позволяет объективно оценить точность результатов исследования. Поскольку невозможно определить вероятность включения в выборку каждого отдельного элемента, полученные результаты нельзя статистически распределять на всю совокупность. Например, клиенты торгового центра могут представлять население города или же несколько городов – страну.

В этом случае присутствует целый ряд искажений, которые могут быть как очевидными, так и неочевидными. Например, если применяется метод перехвата в торговом центре, то в выборке будет непропорционально много тех, кто часто ходит в магазин, или тех у кого много свободного времени. Более того, не существует способа количественной оценки полученных искажений, поскольку основа выборки неизвестна, а процедура ее формирования четко не определена. Поэтому чаще всего прибегают к другим методам, таким как квотная выборка.

Квотная выборка (qujta samplinq) – метод выборки, который представляет собой двухэтапную, ограниченную выборку. Первый этап включает создание контрольных групп, или квот, из элементов совокупности. На втором этапе выбор элементов основан на удобстве отбора или мнения исследователя.

Формирование выборки на основе квот (квотный отбор) предполагает предварительное, исходя из целей исследования, определение численности групп респондентов, отвечающих определенным требованиям (признакам). Степень репрезентативности квотной выборки повышается прямо пропорционально степени устойчивости значений тех характеристик, по которым задаются квоты. Например, в целях исследования было принято решение, что в универсаме должно быть опрошено пятьдесят мужчин и пятьдесят женщин. Интервьюер проводит опрос, пока не выберет установленную квоту.

Квотный отбор бывает двух типов:

- априорный отбор (осуществляется интервьюером в соответствии с квотным планом на стадии сбора первичной информации);

- апостериорный отбор (проводится для корректировки выборки: например, при уличном опросе среди ответивших часто имеется перекос по некоторым параметрам (возраст, пол и т.п.). В таком случае можно взвесить полученные результаты, а можно провести выборку из выборки квотным методом)

Преимущества квотного отбора:

- отсутствие необходимости в повторных посещениях

- возможно достижение заданной точности результатов при меньшем объеме выборки (хотя это спорный момент, не все исследователи с этим утверждением согласны).

Объем квотных выборок. Требования к выборке могут быть жесткими и пониженными. Жесткие требования означают полное совпадение пропорций генеральной и выборочной совокупностей по сочетаниям признаков. В этом случае структура выборочной и генеральной совокупностей по заданным параметрам точно совпадают. При использовании пониженных (частичных) требований контролируют лишь совпадение пропорций по каждому параметру отдельно.

Пример, исследуются журналы: «РБК», «Эксперт», «Аргументы и факты» и др., на вопрос: оправдывают ли эти журналы надежды читателей? Цель исследования проводимого среди населения городского райо на Москвы численностью 350 тыс.человек, - определить круг читателей этих журналов. Маркетологи сформировали квотную выборку, включающую тысячу совершеннолетних респондентов. Контрольные характеристики – пол, возраст и национальность. Исходя из структуры взрослого населения, сформированы следующие квоты (табл. 4.2).

Таблица 4.2

Пример организации квотной выборки

Структура генеральной совокупности	Структура выборки
Контрольная характеристика	Процентное соотношение	Процентное соотношение	Количество
Пол
Мужчины
Женщины
Возраст
18-30
31-45
46-60
Старше 60 лет
Национальность
русские
евреи
белорусы
татары
и другие

В этом примере квоты составлены таким образом, что структура выборки соответствует структуре генеральной совокупности. Однако в некоторых ситуациях желательно отобрать больше или меньше элементов с определенными характеристиками. Например, необходимо создать выборку, состоящую только из тех, кто потребляет много данного товара, чтобы деталь­но изучить их поведение. Несмотря на то, что такая выборка нерепрезентативна, она может иметь огромное значение.

Даже если в структуре выборки полностью отражена структура популяции с учетом контрольных характеристик, нет гарантии, что эта выборка репрезентативна. Если характеристика, непосредственно связанная с проблемой исследования и не учтена, то квотная выборка нерепрезентативна. Важные контрольные характеристики часто упускаются из виду в связи с тем, что на практике очень сложно включить большое количество таких характеристик в выборку. Элементы выбираются из каждой квоты, исходя из удобства или на основании мнения исследователя. Значит, существует большая вероятность необъективности при отборе. Интервьюеры могут отправиться в те из указанных районов, где легче всего найти подходящих респондентов. Более того, они могут избегать людей, которые недружелюбно выглядят, плохо одеты или живут в местах, куда неудобно добираться. Квотная выборка не позволяет оценить величину ошибки выборки.

Применяя выборку по квотам, исследователь стремится получить представительную выборку при сравнительно низком уровне затрат. Преимущества такой выборки - ее низкая стоимость и удобство выбора элементов для каждой квоты. В последнее время введен более жесткий контроль за действиями интервьюеров и процедурами проведения опроса, что позволяет уменьшить искажения при отборе. Предложены меры по улучшению качества выборок по квотам при проведении интервью в торговых центрах. При определенных условиях применение выборки по квотам дает результаты, похожие на результаты применения случайно выборки.

Иногда у исследователей возникает соблазн увеличить число контролируемых квотных параметров в надежде на повышение степени достоверности результатов. Однако на практике это ведет к нарастанию систематической ошибки и затрудняет полевую работу интервьюера.

Гнездовая выборка. Определяются группы (гнезда) потребителей по месту проживания (кварталы), по местам работы, отдыха и д.р., составляются их списки, а затем проектируется выборка. Метод основывается на принципе суждения, т.е на использовании мнения квалифицированных специалистов, экспертов относительно состава выборки. На основе такого подхода часто формируется состав фокус-группы.

Гнездовая выборка (кластерная, серийная). Здесь отбираются не объекты исследования (например, люди), а группы. Группы отбираются случайным образом, а внутри них проводится сплошной опрос. Например, в ВУЗе с большим количеством студенческих групп отбор можно проводить путем случайного отбора этих групп и дальнейшего сплошного опроса в этих группах.

Ясно, что доверительный интервал при гнездовой выборке будет меньше (выборка точней) при той же надежности чем при случайной, т.к. межгрупповая дисперсия меньше общей дисперсии. Внутригрупповая дисперсия нам не нужна, т.к. мы опрашиваем все гнездо целиком и поэтому отклонения выборочного показателя от генерального внутри этой группы не имеем. Следовательно, нас должно волновать то, правильно ли мы выбрали сами группы. Поэтому мы и учитываем лишь межгрупповую дисперсию.

Например, составление опросного списка на 1000 чел. (размер выборки) для изучения общественного мнения населения города Москвы. Не располагая списком всех жителей города, можно было бы начать с получения карты города, чтобы определить все его кварталы и составить их список. Список кварталов становится основой выборки, из которой случайным образом или систематически производится выборка кварталов. Затем проектируется выборка жилых домов из каждого квартала, устанавливается связь с семьями, проживающими в отобранных домах, и у представителя каждой семьи берется интервью для опросного листа. Предположим, есть 500 кварталов; из них случайным образом отобрано 25. В этих кварталах идентифицированы 4000 семей. Связь устанавливается с 25% этих семей, потому что требуется выборка из 1000 индивидов, т.е. (4000 семей × 0,25 = 1000). Эти представители 1000 семей отбираются случайным или систематическим образом.

Метод «снежного кома». Применяется для отбора экспертов и редко встречающихся групп респондентов («редких элементов»), например, потребителей, обладающих очень высокими доходами, или представителей элитных групп. По сути это техника поиска и отбора респондентов с определенным сочетанием свойств в таких условиях, когда трудно очертить границы генеральной совокупности. Особенность метода в том, что за исключением первого шага, выбор каждого очередного респондента совершается по указанию респондентов, включенных в состав выборки на предыдущем шаге. Каждый из респондентов указывает интервьюеру, где можно найти интересующих последнего людей (иногда даже сам связывается с ними и рекомендует интервьюера), и выборка с каждым шагом разрастается подобно снежному кому, т.е. – это метод согласно которому случайным образом побирается начальная группа респондентов. В дальнейшем отбор осуществляется из числа кандидатов, указанных первыми респондентами, или на основе предоставленной ими информации. Данный процесс проходит волнообразно, когда респонденты, прошедшие опрос называют следующих кандидатов и т.д.

Стихийные выборки формируются произвольно, причем часто независимо от самого исследователя. Примерами стихийного отбора могут служить опросы с помощью средств массовой информации, выборка «первого встречного», опросы покупателей в залах супермаркетов, пассажиров на остановках и в общественном транспорте и т.д. Одна из особенностей стихийной выборки состоит в том, что зачастую невозможно заранее предсказать ее размеры (например, при опросах с помощью СМИ), — достаточно вспомнить опросы, проводимые с помощью интерактивного телевидения.

4.4. Многоступенчатая выборка

Многоступенчатая выборка - тип вероятностной выборки или метод отбора, при котором на каждой, кроме последней, ступени построения выборки объекты группируются в некоторые структурные единицы (кластеры), среди которых и производится отбор. На последней ступени выборки кластеры, прошедшие все этапы отбора, обследуются полностью или выборочно.

Многоступенчатая выборка - осуществляется в несколько этапов:

- на первом этапе производится расчленение крупных общностей;

- на последующих этапах внутри этих общностей вычленяются меньшие по объему. При этом совокупность объектов, отобранных напредыдущем этапе, становится исходной для отбора на следующем этапе. Промежуточные объекты, составляющие выборочную совокупность на высших ступенях, называют единицами отбора. Соответственно различают единицы отбора первой ступени (первичные единицы), единицы отбора второй ступени (вторичные единицы) и т.д. К единицам отбора можно отнести отрасль предприятия, номенклатуру выпускаемой продукции, ценовой диапазон, имидж и др.

Объекты нижней ступени, обеспечивающие непосредственный сбор информации, называются единицами наблюдения. Единицами наблюдения (test units) являются объекты, составляющие генеральную совокупность (являющиеся ее элементами), могут быть индивидуумы, организации либо иные наблюдаемые объекты, чья реакция на независимые факторы изучается. Единицы наблюдения могут включать потребителей, магазины, географические зоны и т.д. Непосредственный отбор единиц наблюдения производится только на последней ступени многоступенчатой выборки. На всех предшествующих ступенях производится отбор кластеров, которые объединяют некоторое количество единиц наблюдения, но сами являются только единицами отбора.

Многоступенчатую выборку рекомендуется применять:

- если генеральная совокупность велика и имеет сложную многоуровневую структуру;

- если средства на исследование ограничены;

- если в разных частях генеральной совокупности целесообразно применять различные методы отбора.

Приведем пример многоступенчатой выборки, которая была проведена в Москве в маркетинговом центре. По данным статистики стоимость таких исследований для одного заказчика составила 15000 руб. за вопрос в зависимости от темы и общего объема выборки. Для г.Москвы объем выборки был задан в 900 чел. В качестве единицы отбора первой ступени были определены три городских района из восьми с объемом выборки 300 респондентов по каждому. Здесь, как и на следующей ступени был использован метод типовых представителей. Определив среднюю численность населения одного района исследователи остановили свой выбор на трех районах, численность населения которых в наименьшей степени отклонялась от этого среднего значения.

За основу выборки на второй ступени были взяты списки респондентов. В качестве единицы отбора второй ступени были определены три квартала и были рассчитаны средние размеры каждого квартала и отобраны те, где численность населения в наименьшей степени отклонялось от средней. На третьей ступени за основу выборки принимался список жителей каждого квартала. Было определено, что в каждом квартале предстоит опросить по 100 чел. (n=100). На этом последнем этапе для окончательного отбора единиц наблюдения применялся метод систематической выборки. Определив шаг выборки, можно получить списки респондентов с домашними адресами. Поскольку для всех районов имелись электронные версии списков респондентов. Вся процедура решения проблемы по данному направлению заняла менее двух дней.

4.5. Определение объема выборки

Процедура составления плана выборки включает последовательное решение трех следующих задач:

- определение объекта исследования;

- определение структуры выборки;

- определение объема выборки.

Как правило, объект маркетингового исследования представляет собой совокупность объектов наблюдения, в качестве которых могут выступать потребители, сотрудники компании, посредники и т.д. Если эта совокупность настолько малочисленна, что исследовательская группа располагает необходимыми трудовыми, финансовыми и временными возможностями для установления контакта с каждым из ее элементов, то вполне реально проведение сплошного исследования всей совокупности. В этом случае, определив объект исследования, можно приступать к следующей процедуре (выбору метода сбора данных, орудия исследования и способа связи с аудиторией).

Однако на практике очень часто не представляется возможным или целесообразным проведение сплошного исследования всей совокупности. Для этого могут быть следующие причины:

-невозможность установления контакта с некоторыми элементами совокупности;

-неоправданно большие расходы на проведение сплошного исследования или наличие финансовых ограничений, не позволяющих проведение сплошного исследования;

-сжатые сроки, отведенные для исследования, обусловленные утратой со временем актуальности информации или другими причинами и не позволяющие осуществить сбор, систематизацию и анализ обширных данных для всей совокупности.

Поэтому большие и разбросанные совокупности часто изучаются с помощью выборки, под которой, как известно, понимается часть совокупности, призванная олицетворять совокупность в целом.

Точность, с которой выборка отражает совокупность в целом, зависит от структуры и размера выборки.

Различают два подхода к структуре выборки — вероятностный и детерминированный.

Вероятностный подход к структуре выборки предполагает, что любой элемент совокупности может быть выбран с определенной (не нулевой) вероятностью. Существуют различные виды выборок, основанных на теории вероятностей (типическая, гнездовая и др.). Наиболее простой и распространенной на практике является простая случайная выборка, при которой каждый элемент совокупности имеет равную вероятность выбора для исследования.

Вероятностная выборка более точна, позволяет исследователю оценить степень достоверности собранных им данных, хотя она сложней и дороже, чем детерминированная.

Детерминированный подход к структуре выборки предполагает, что выбор элементов совокупности производится методами, основанными либо на соображениях удобства, либо на решении исследователя, либо на контингентных группах.

Метод формирования выборки, основанный на соображениях удобства, состоит в выборе любых элементов совокупности исходя из простоты установления контакта с ними. Несовершенство этого метода обусловлено, возможно, низкой репрезентативностью полученной выборки, т.к. удобные для исследователя элементы совокупности могут быть недостаточно характерными представителями совокупности в силу неслучайного и необоснованного их отбора.

Однако, с другой стороны, простота, экономичность и оперативность исследования, проводимого этим методом, снискали ему довольно широкое распространение на практике и, прежде всего при проведении предварительных исследований, направленных на уточнение основных проблем.

Метод формирования выборки, основанный на решении исследователя, состоит в выборе элементов совокупности, которые, по его мнению, являются ее характерными представителями. Этот метод является более совершенным, чем предыдущий, поскольку в его основе лежит ориентировка на характерных представителей исследуемой совокупности, хотя и подбираемых на основе субъективных представлений исследователей о ней.

Метод формирования выборки, основанный на контингентных нормах, состоит в выборе характерных элементов совокупности в соответствии с полученными ранее характеристиками совокупности в целом. Эти характеристики могут быть получены путем проведения предварительных исследований и в отличие от предыдущего метода не носят субъективного характера. Поэтому данный метод является более совершенным, он позволяет получить выборочные совокупности не менее представительные, чем вероятностные выборки при значительно меньших затратах на проведение обследования.

Выбрав структуру выборки (подход к ее формированию, вид вероятностной или метая формирования детерминированной выборки), исследователю предстоит определить объем, т.е. количество элементов выборочной совокупности.

Объем выборки определяет достоверность информации, полученной в результате ее исследования, а также необходимые для проведения исследования затраты. Объем выборки зависит от уровня однородности или разновидности изучаемых объектов.

Чем больше объем выборки, тем выше ее точность и больше затраты на проведения ее обследования. При вероятностном подходе к структуре выборки ее объем может быть определен с помощью известных статистических формул, на основе заданных требований к ее точности.

На практике используется несколько подходов к определению объема выборки:

1. Произвольный подход основан на применении «правила большого пальца». Например, бездоказательно принимается, что для получения точных результатов выборка должна составлять 5 % от совокупности. Данный подход является простым и легким в исполнении, однако не представляется возможным установить точность полученных результатов. При достаточно большой совокупности он к тому же может быть и весьма дорогим.

Объем выборки может быть установлен исходя из неких заранее оговоренных условий. К примеру, заказчик маркетингового исследования знает, что при изучении общественного мнения выборка обычно составляет 1000-1200 человек, поэтому он рекомендует исследователю придерживаться данной цифры. В случае, если на каком-то рынке проводятся ежегодные исследования, то в каждом году используется выборка одного и того же объема. В отличие от первого подхода здесь при определении объема выборки используется известная логика, которая, однако, является весьма уязвимой.

Например, при проведении определенных исследований может потребоваться точность меньше, чем при изучении общественного мнения, да и объем совокупности может быть во много раз меньше, нежели при изучении общественного мнения. Таким образом, данный подход не принимает в расчет текущие обстоятельства и может быть достаточно дорогим.

В ряде случаев в качестве главного аргумента при определении объема выборки используется стоимость проведения обследования. Так, в бюджете маркетинговых исследований предусматриваются затраты на проведение определенных обследований, которые нельзя превышать. Очевидно, что ценность получаемой информации не принимается в расчет. Однако в ряде случаев и малая выборка может дать достаточно точные результаты.

Представляется разумным учитывать затраты не абсолютным образом, а по отношению к полезности информации, полученной в результате проведенных обследований. Заказчик и исследователь должны рассмотреть различные объемы выборки и методы сбора данных, затраты, учесть другие факторы

2. Объем выборки от уровня доверительного интервала допустимой ошибки, каковая, как уже говорилось, задается целесообразной точностью итоговых обобщений: от повышенной до ориентировочной. Однако здесь имеются в виду так называемые случайные ошибки, связанные с природой любых статистических погрешностей. Именно они и вычисляются как ошибки репрезентативности вероятностных выборок.

В. И. Паниотто приводит следующие расчеты репрезентативной выборки с допущением 5-процентной ошибки (табл. 4.2).

Таблица 4.2

Расчетная таблица выборки

Объем генеральной совокупности
Объем выборки
Объем генеральной совокупности
Объем выборки

Для совокупности более 100000 выборка составляет 400 единиц. Если же иметь в виду генеральные совокупности численностью от 5 тыс. и больше, то, по расчетам того же автора, можно указать величины фактической ошибки выборки в зависимости от ее объема, что для нас весьма важно, памятуя, что величина допустимой ошибки зависит от цели исследования и необязательно должна приближаться к 5-процентному уровню.

Таблица 4.3

Расчетная таблица

Объем выборки, если генеральная совокупность ³ 5000								625...
Фактическая ошибка при данном объёме выборки, %

Наряду со случайными возможны ошибки систематического характера. Они зависят от организации выборочного обследования. Это разнообразные смещения выборки в сторону одного из полюсов выборочного параметра.

3. Объем выборки на основе статистического анализа. Этот подход основан на определении минимального объема выборки исходя из определенных требований к надежности и достоверности получаемых результатов. Он также используется при анализе полученных результатов для отдельных подгрупп, формируемых в составе выборки по полу, возрасту, уровню образования и т.п. Требования к надежности и точности результатов для отдельных подгрупп диктуют определенные требования к объему выборки в целом.

Наиболее теоретически обоснованный и корректный подход к определению объема выборки основан на расчете достоверных интервалов. Понятие вариации характеризует величину несхожести (схожести) ответов респондентов на определенный вопрос. В более строгом плане вариацией значений какого-либо признака в совокупности называется различие его значений у разных единиц данной совокупности в один и тот же период или момент времени. Результаты ответов на вопросы опроса обычно представляются в форме кривой распределения (рис. 4.1). При высокой схожести ответов говорят о малой вариации (узкая кривая распределения) и при низкой схожести ответов – о высокой вариации (широкая кривая распределения).

В качестве меры вариации обычно принимается среднее квадратическое отклонение, которое характеризует среднее расстояние от средней оценки ответов каждого респондента на определенный вопрос.

Малая вариация

Высокая вариация

Рис. 4.1. Вариация и кривые распределения

Поскольку все маркетинговые решения принимаются в условиях неопределенности, то это обстоятельство целесообразно учесть при определении объема выборки. Так как определение исследуемых величин для совокупности в узком осуществляется на основе выборочной статистики, то следует установить диапазон (доверительный интервал), в который, как ожидается, попадут оценки для совокупности в целом, и ошибку их определения.

Доверительный интервал – это диапазон, крайним точкам которого соответствует определенный процент определенных ответов на какой-то вопрос. Доверительный интервал тесно связан со средним квадратическим отклонением изучаемого признака в генеральной совокупности: чем оно больше, тем шире должен быть доверительный интервал, чтобы включить в свой состав определенный процент ответов.

Доверительный интервал, равный или 95 %, или 99 %, является стандартным при проведении маркетинговых исследований. Ни одна фирма не проводит маркетинговых исследований, формируя несколько выборок. И математическая статистика дает возможность получить некую информацию о выборочном распределении, владея только данными о вариации единственной выборки.

Индикатором степени отличия оценки, истинной для совокупности в целом, от оценки, которая ожидается для типичной выборки, является средняя квадратическая ошибка. Причем, чем больше объем выборки, тем меньше ошибка. Высокое значение вариации обусловливает высокое значение ошибки и наоборот.

Когда на заданный вопрос существует только два варианта ответа, выраженные в процентах (используется процентная мера), объем выборки определяется по следующей формуле:

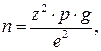
где n – объем выборки; z – нормированное отклонение, определяемое исходя из выбранного уровня доверительности; p – найденная вариация для выборки; g – (100-р); е – допустимая ошибка.

При определении показателя вариации для определенной совокупности прежде всего целесообразно провести предварительный качественный анализ исследуемой совокупности, в первую очередь установить схожесть единиц совокупности в демографическом, социальном и других отношениях, представляющих интерес для исследователя. Возможно проведение пилотного исследования, использование результатов подобных исследований, проведенных в прошлом. При использовании процентной меры изменчивости принимается в расчет то обстоятельство, что максимальная изменчивость достигается для р = 50 %, что является наихудшим случаем. К тому же этот показатель радикальным образом не влияет на объем выборки. Учитывается также мнение заказчика исследования об объеме выборки.

Возможно определение объема выборки на основе использования средних значений, а не процентных величин.

где s – среднее квадратическое отклонение.

На практике, если выборка формируется заново и схожие опросы не проводились, то s не известно. В этом случае целесообразно задавать погрешность е в долях от среднеквадратического отклонения. Расчетная формула преобразуется и приобретает следующий вид:

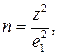где .

Выше шел разговор о совокупностях очень больших размеров. Однако в ряде случаев совокупности не являются большими. Обычно, если выборка составляет менее пяти процентов от совокупности, то совокупность считается большой и расчеты проводятся по вышеприведенным правилам. Если объем выборки превышает 5 % от совокупности, то последняя считается малой и в вышеприведенные формулы вводится поправочный коэффициент.

Объем выборки в данном случае определяется следующим образом:

,

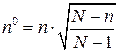где n - объем выборки для малой совокупности; n⁰ – объем выборки, рассчитанный по приведенным выше формулам; N – объем генеральной совокупности.

Очевидно, что использование выборки меньших размеров приведет к экономии времени и средств.

Приведенные формулы расчета объема выборки основаны на предположении, что все правила формирования выборки были соблюдены и единственной ошибкой выборки является ошибка, обусловленная ее объемом. Однако, следует помнить, что объем выборки определяет точность полученных результатов, но не их представительность.

Последняя определяется методом формирования выборки. Все формулы для расчета объема выборки предполагают, что репрезентативность гарантируется использованием корректных вероятностных процедур формирования выборки.

Объем, выборки определяется аналитическими, задачами исследования, а ее репрезентативность — целевой установкой программы. Именно программа задает образ необходимой генеральной совокупности для проведения выборки. Будет ли это все население или особые его структурные образования, все элементы изучаемого объекта или только выделяемые по заданным программой критериям, генеральную совокупность составляют все единицы, определенного в программе объекта.

При детерминированном подхода к структуре выборки в общем случае не представляется возможным расчетным путем точно определить ее объем в соответствии с заданным критерием достоверности полученной информации. В этом случае объем выборки может быть определен эмпирически. Ориентиром здесь может служить опыт проведения маркетинговых исследований за рубежом. Так, при обследовании покупателей высокая точность выборки обеспечивается, даже если ее объем не превышает 1% всей совокупности при проведении опросов покупателей средних и крупных розничных фирм, количество опрашиваемых (объем выборки), как правило, колеблется от 500 до 1000 человек.

Значение процедуры выбора метода сбора первичной информации, и орудия исследования состоит в том, что результаты этого выбора определяют как достоверность и точность подлежащей сбору информации, так и продолжительность, и дороговизну ее сбора.

Контрольные вопросы к главе 4

1. Дайте определение выборки.

2. На каких принципах основаны метод и процедура выборки?

3. В чем заключается метод вероятностной выборки?

4. Как рассчитывается шаг выборки «к»?

5. Что понимается под методом систематической выборки?

6. Что такое стратифицированная выборка?

7. Дайте определение генеральной совокупности.

8. Изложите сущность невероятностной (неслучайной) выборки.

9. Какие два основных вида неслучайного отбора Вы знаете?

10. Какие методы выборки относят к направленному отбору?

11. В чем заключается сущность методов: типовых представителей, квотной и гнездовой выборки, метода смежного кома?

12. Изложите сущность стихийной выборки.

13. Опишите процедуру гнездовой (кластерной) выборки.

14. В каких случаях лучше использовать многоступенчатую выборку?

15. Дайте определение систематической выборки.

Глава 5. ПОТРЕБИТЕЛЬ В МАРКЕТИНГОВЫХ ИССЛЕДОВАНИЯХ

Дата добавления: 2015-03-31