Анализ и обработка экспертных оценок

Анализ и обработка экспертных оценок. При проведении анализа собранных экспертных данных в соответствии с целями исследования и принятыми моделями необходимо определить согласованность действий экспертов и достоверность экспертных оценок.

Метод Дельфи может быть применен в процессе группового принятия управленческого решения посредством выбора наилучшей альтернативы. Результаты экспертных оценок заносятся в таблицу (см. табл. 7.38), где Р - ранговая оценка, присваиваемая экспертом альтернативе в зависимости от степени ее значимости. Наиболее значимая альтернатива, например, решение сменить поставщика, ставится на первое место (1 ранг); Б — балльная оценка дается экспертом от 1 до 10 баллов. За наивысший балл берется единица. Итоговое значение П = Р∙Б. По каждой альтернативе определяется сумма произведений. Наибольшая сумма по столбцам П указывает на значимую альтернативу принятия решения.

Таблица 7.38

Распределение экспертных оценок методом Дельфи

Ф.И.О. эксперта

Альтернативы

Р

Б

П

Р

Б

П

Р

Б

П

Р

Б

П

1.

2.

3.

…

Итого:

∑Пi1

∑Пi2

∑Пi3

∑Пi4

Метод средневзвешенных критериев является эффективным для оценки экспертами ряда альтернатив и вариантов слабо структурированных решений. Система взвешенных критериев может быть применена, например, для оценки при выборе поставщиков продукции. На первом этапе экспертами дается оценка непосредственно критериев выбора. На последнем этапе определяется суммарное взвешивание вариантов с учетом разной «весовой» категории каждого критерия, т.е. перемножаются весовые показатели критериев выбора на взвешенные варианты по каждой строке (табл. 7.39).

Таблица 7.39

Оценка поставщика в баллах (1-10)

Критерии выбора	Вес (ранг) критерия	Поставщики
1.	Р1	Б11	П11	Б21	П21	Б31	П31
2.	Р2	Б12	П12	Б22	П22	Б32	П32
3.	Р3	Б13	П13	Б23	П23	Б33	П33
Итого:			∑Пi		∑Пi		∑Пi

Максимальное значение суммарной взвешенной оценки показывает наиболее адекватную оценку фирмы-поставщика.

Ранжирование объектов маркетинговых исследований. Расположение этих факторов в порядке возрастания или убывания какого-либо присущего им свойства, называется ранжированием. Ранжирование позволяет выбрать из исследуемой совокупности факторов наиболее существенный.

При ранжировании эксперт должен расположить объекты (альтернативы) в порядке, который представляется ему наиболее рациональным, и приписать каждому из них числа натурального ряда - ранги. При этом ранг 1 получает наиболее предпочтительная альтернатива, а ранг N - наименее предпочтительная. Следовательно, порядковая шкала, получаемая в результате ранжирования, должна удовлетворять условию равенства числа рангов N числу ранжируемых объектов п.

Бывает так, что эксперт не в состоянии указать порядок следования для двух или нескольких объектов либо он присваивает разным объектам один и тот же ранг, и в результате число рангов N оказывается не равным числу ранжируемых объектов п. В таких случаях объектам приписывают так называемые стандартизированные ранги. С этой целью общее число стандартизированных ран­гов полагают равным п, а объектам, имеющим одинаковые ранги, присваивают стандартизированный ранг, значение которого представляет среднее суммы мест, поделенных между собой объектами с одинаковыми рангами.

Пусть, например, шести объектам (альтернативам, факторам) экспертами присвоены следующие ранги (табл. 7.40).

Таблица 7.40

Исходные результаты экспертного анализа

Номер объекта
Ранг

Тогда объектам 1 и 5, поделившим между собой первое и второе место, приписывается стандартный ранг (вес) R= (1+2)/2=1,5, а объектам 2 и 3, поделившим третье и четвертое место R=(3+4)/2=3,5. В итоге получаем следующую ситуацию ранжирования (табл. 7.41).

Таблица 7.41

Таблица ранжирования

Номер объекта - n
Ранг - ri	1,5	3,5	3,5		1,5

Таким образом, сумма рангов R_n, полученная в результате ранжирования n объектов, будет равна сумме чисел натурального ряда, т.е.

R_n = Sr_i = n(n+1)/2.

Когда ранжирование производится несколькими (т) экспертами, сначала для каждого объекта подсчитывают сумму рангов R_{ij =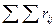} , полученную от всех экспертов, а затем исходя из этой величины устанавливают результирующий ранг для каждого объекта. Наивысший (первый) ранг присваивают объекту, получившему наименьшую сумму рангов, и, наоборот, объекту, получившему наибольшую сумму, рангов, присваивают самый низкий ранг N. Остальные объекты упорядочивают в соответствии со значением суммы рангов относитёльно объекта, которому присваивается первый ранг.

Точность и надежность процедуры ранжирования в значительной степени зависят от количества объектов. В принципе чем таких объектов меньше, тем выше их «различимость» с точки зрения эксперта, а следовательно, тем более надежно можно установить ранг объекта, Во всяком случае количество ранжируемых объектов п не должно быть больше 20, а наиболее надёжна эта про­цедура, когда n < 10.

Метод ранжирования редко используется «в чистом виде». Чаще всего он сочетается с другими методами, обеспечивающими более четкое различие между факторами. Одним из них является метод непосредственной оценки и некоторые его модификации.

Например, m экспертов оценили по шкале от 0 до 100 k направлений исследований, с точки зрения важности их для достижения определенной цели.

Для того чтобы проранжировать эти оценки, приписываем каждому из направлений число натурального ряда таким образом, чтобы ранг 1-был приписан максимальной оценке, а ранг k - минимальной (табл. 7.42).

Таблица 7.42

Перевод оценок в ранги

Направления исследований
Оценка
Ранг

В ряде случаев суммарные оценки рангов нормируются. Нормирование любой меры означает, что представляющее ее число для всего множества в целом принимается равным единице. Нормирование позволяет устано­вить более тесную связь между оценками, приписанными экспертами отдельным объектам. С этой целью оценки по всем объектам суммируются, а затем каждая из них делится на полученную сумму. Рассчитанные таким образом нормированные оценки могут быть вновь проранжированы.

Когда в экспертизе участвует несколько экспертов, обычно стремятся получить усредненную оценку (вес) для каждого объекта. Для этого нормированные оценки каждого объекта суммируются, а затем полученная сумма делится на число экспертов.

При наличии нескольких факторов, по которым следует оценить каждый из объектов, средняя оценка p_i (вес) каждого объекта может быть рассчитана по формуле

,

где p_ij – вес i объекта, подсчитанный по оценкам всех экспертов.

,

где x_ij - оценка фактора i, данная экспертом j; п - число факторов; т - число экспертов.

Другой способ установления зависимости между оценками факторов (объектов, характеристик) состоит в том, что важнейшему (с точки зрения экспертов) фактору назначается оценка (вес), равная наперед заданному числу (обычно 1 или 10), а оценка следующих друг за другом по важности факторов определяется последовательно как доля, более важного. Полученные таким образом значения нормируются. Основное достоинство такого способа заключается в том, что он облегчает процесс выбора оценок, поскольку эксперту не нужно каж­дый раз сопоставлять весь их ряд, а лишь учитывать значение первой и предыдущей по важности оценок. Оценки, полученные от группы экспертов, могут быть усреднены для каждого фактора путем расчета средней арифметической.

В случаях когда группа, состоящая из нескольких экспертов, оценивает ряд факторов, причем у каждого из экспертов имеется своя шкала предпочтений, для нахождении усредненной оценки каждого фактора может быть рекомендована следующая методика.

1. Составляется матрица «эксперты - факторы», в которой проставляются полученные от каждого эксперта оценки факторов по шкале от 0 до 10 (представим, что два эксперта оценили шесть факторов так, как показано в табл. 7.43).

Таблица 7.43

Оценка факторов

Эксперт	Факторы
				Итого

2. Рассчитывается относительная значимость (p) всех факторов в отдельности для каждого эксперта. С этой целью оценки, полученные от каждого эксперта, суммируются (по горизонтали), а затем нормируются:

p₁₁ = 8/30; p₂₁=6/30; p₃₁=9/30; p₄₁=7/30;

p₁₂=10/33; p₂₂=8/33; p₃₂=9/33; p₄₂=6/33.

3. Вычисляется усредненная оценка, данная всеми экспертами каждому фактору. Для этого нормированные оценки, полученные в предыдущем шаге, суммируются (по вертикали), а затем рассчитывается средняя ариф­метическая для каждого фактора:

p₁=(8/30+10/33)/2=0,285;

p₂=(6/30+8/33)/2=0,236;

p₃=(9/30+9/33)/2=0,286;

p₄=(7/30+6/33)/2=0,207.

Рассмотрим применение методов экспертных оценок для анализа конкретных маркетинговых ситуаций. Например, необходимо дать оценку степени привлекательности двух локальных товарных рынков (табл. 7.44).

Таблица 7.44

Данные оценки рынка

Критерии привлекательности рынка	Относительная важность критерия	Экспертная оценка	Взвешенная оценка
Рынок	Рынок
1. Размер рынка	0,3			1,5	0,9
2. Скорость роста рынка	0,25			2,0	2,25
3. Легкость входа и выхода	0,15			0,3	0,6
4. Прибыльность	0,3			2,7	2,1
Итого:	1,0			6,5	5,85

Из таблицы 7.44 видно, что рынок 1 по взвешенной оценке привлекательнее рынка 2 в 6,5/5,85=1,11 или на 11%.

Рассмотрим еще пример применения экспертных методов. Необходимо дать оценку силы бизнеса фирмы «А» и «Б», действующих на товарном рынке города «С» (табл. 7.45).

Таблица 7.45

Оценка силы бизнеса

Критерии силы бизнеса	Относительная важность критерия	Экспертная оценка	Взвешенная оценка
А	Б	А	Б
1. Доля рынка	0,3			1,5	2,1
2. Конкурентная цена	0,15			1,35	0,9
3. Использование инвестиций	0,25			1,0	0,5
4. Эффективность продвижения	0,2			1,8	1,0
5. Квалификация персонала	0,1			0,8	0,6
Итого:	1,0			5,27	5,1

Из итоговой графы взвешенной оценки видно, что бизнес фирмы «А» выглядит более внушительно, чем бизнес фирмы «В».

Рассмотрим следующий пример. Эксперту нужно оценить 5 видов хлеба по 10 показателям и выбрать наилучший вариант для реализации. Каждый показатель оценивается по 5-балльной шкале (табл. 7.46).

Таблица 7.46

Экспертная оценка предпочтений атрибутов хлеба разных марок

Параметры	Вид хлеба
1. Вес
2. Сорт
3. Качество
4. Цена
5. Упаковка
6. Экологичность
7. Вкус
8. Производитель
9. Энергетическая ценность
10. Срок хранения
Общая сумма баллов

Подобная оценка товаров неполна, поэтому для большей объективности вводятся весовые коэффициенты предпочтения – частные критерии качества (ЧКК). Для получения ЧКК построим матрицу бинарных предпочтений (табл. 7.47) по исходной табл. 6.46. Доминирование частного критерия запишется единицей, отсутствие доминирования – нуль.

Таблица 7.47

Матрица бинарных предпочтений

ЧКК	К1	К2	К3	К4	К5	К6	К7	К8	К9	К10	сi	Vj
К1	-											0,09
К 2		-										0,13
К 3			-									0,11
К 4				-								0,16
К5					-							0,07
К6						-						0,18
К7							-					0,2
К8								-				0,04
К9									-			0,02
К10										-

Параметры матрицы: c_i – сумма значений строки по i -у критерию, ∑ с_i =1, V_j = c_ij/∑c_j

В этом случае весовые критерии значимости оценивают по матрице бинарных предпочтений, предварительно проведя ранжирование параметров по степени их значимости: К₇ >К₆>К₄>К₂>К₃>К₁>К₅>К₈>К₉>К_10.

В обработке значений имеются параметры в направлении к экстремуму в сторону максимизации или минимизации. Величина - относительный показатель качества, может принимать различные значения.

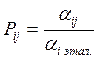, если направление экстремума – max;

, если направление экстремума – min,

где - численное значение i -го ЧКК по j -му товару; 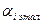- эталонное значение i -го показателя.

В таблице 7.48 представлены количественные оценки представленных 5 видов хлеба, а также оценки эталонного параметра по видам хлеба с указанием направления экстремума.

Таблица 7.48

Расчетная таблица

Параметры	Вид хлеба	Эталон	Направление экстремума
1. Вес	0,4	0,3	0,35	0,45	0,5	0,5	max
2. Сорт							max
3. Качество							max
4. Цена, руб.		9,5		11,5	8,5		min
5. Упаковка							max
6. Экологичность							max
7. Вкус							max
8. Упаковка							max
9. Энергетическая ценность							min
10. Срок хранения, сут.							max

По данным табл. 7.48 осуществим расчет перехода от количественных оценок к относительным показателям:

Р₁₁ = 0,4/0,5=0,8 Р₂₁ = 1/5=0,2

Р₁₂ = 0,3/0,5=0,6 Р₂₂ = 3/5=0,6

Р₁₃ = 0,35/0,5=0,7 Р₂₃ = 4/5=0,8

Р₁₄ =0,45/0,5=0,9 Р₂₄ =5/5=1

Р₁₅ = 0,5/0,5=1 Р₂₅ = 2/5=0,4

Р₃₁ = 2/5=0,4 Р₄₁ = 10/10=1

Р₃₂ = 4/5=0,8 Р₄₂ = 9,5/10=0,95

Р₃₃ = 5/5=1 Р₄₃ = 8/10=0,8

Р₃₄ =3/5=0,6 Р₄₄ =11,5/10=1,15

Р₃₅ = 1/5=0,2 Р₄₅ = 8,5/10=0,85

Р₅₁ = 4/5=0,8 Р₆₁ = 0,9

Р₅₂ = 5/5=1 Р₆₂ =0,9

Р₅₃ = 1/5=0,2 Р₆₃ = 1

Р₅₄ =2/5=0,4 Р₆₄ = 0,9

Р₅₅ = 3/5=0,6 Р₆₅ = 0,8

Р₇₁ =0,2 Р₈₁ = 0,43 Р₉₁ = 0,92 Р₁₀₁ = 1

Р₇₂ = 0,6 Р₈₂ = 0,71 Р₉₂ = 1 Р₁₀₂ = 0,67

Р₇₃ = 0,8 Р₈₃ = 1 Р₉₃ = 1,08 Р₁₀₃ = 1,33

Р₇₄ =1 Р₈₄ =0,57 Р₉₄ = 1,15 Р₁₀₄ = 0,33

Р₇₅ = 0,4 Р₈₅ = 0,29 Р₉₅ = 0,96 Р₁₀₅ = 0,67

Для получения аддитивной скалярной оценки качества используют следующую формулу

Q_j = (1- P_ij)·(1-V_j),

где P_ij – относительный показатель качества, V_i – вес или степень значимости i -го ЧКК. Тогда для марки хлеба:

Q₁ = (1- 0,8)·(1 – 0,09)+(1- 0,2)·(1- 0,13)+(1- 0,4)·(1- 0,11)+(1- 1)·(1-0,16)+ (1- 0,8)·(1- 0,07)+(1- 0,9)·(1- 0,18)+(1- 0,2)·(1- 0,2)+(1- 0,43)·(1- 0,04)+(1- 0,92) (1- 0,02)+(1-1)·(1-0) = 0,2·0,91+0,8·0,87+0,6·0,89+0,2·0,93+ 0,1·0,82+ 0,8·0,8+ 0,57·0,96+ 0,08·0,98 = 2,945.

Q₂ = (1- 0,6)·(1- 0,09)+ (1- 0,6)·(1- 0,13)+ (1- 0,8)·(1- 0,11)+(1- 0,95)·0,84+ +(1- 0,9)·0,82+(1-0,6)·0,8+(1- 0,71)·0,96 = 1,942.

Q₃ = 0,3·0,91+0,2·0,87+0,2·0,84+0,8·0,93+0,2·0,8-0,08·0,98-0,33 = 1,111. Q₄ = 0,1·0,91+ 0,4·0,89- 0,15·0,84 + 0,6·0,93+ 0,1·0,82+ 0,43·0,96- 0,15·0,98+0,67= 1,627.

Q₅ = 0,6·0,87+0,8·0,89+0,15·0,84+0,4·0,93+0,2·0,82+0,6·0,8+0,71·0,96+ +0,04·0,98+ 0,33 = 3,434.

Из приведённых расчётов следует, что образец хлеба №3 («Ароматный») наиболее качественный из 5 предложенных, т.к. относительная оценка качества ближе к эталону (Q_эт. = 0), чем остальные образцы.

Обратные значения Q_i будут определять структурную долю марок хлеба в магазинной секции, т.е. Si=1-Qi/∑Qi, что видно из табл. 7.49.

Таблица 7.49

Структура ассортимента хлеба

	«Нива»	«Русское поле»	«Ароматный»	«Городской»	«Экстра»	∑
Q	2,945	1,942	1,111	1,627	3,434	11,06
S	0,73	0,825	0,9	0,853	0,689	3,997
Si	0,175	0,206	0,225	0,213	0,172	1,0

Если экспертизу осуществляют несколько экспертов, то необходимо оценивать их на согласованность мнений. Рассмотрим следующий пример. Для решения проблем закупки марок хлеба проведем экспертный анализ 5 продавцов секции «хлеб». Для оценки правильности выводов, рассчитаем коэффициент конкордации и по его значению примем решение. Пусть число товаров (сортов хлеба) равно 7. Решение представим в таблице 7.50.

Таблица 7.50

Эксперт, N	Марки производителей хлеба, m
1
2
3
4
5
ri
di	-1	-11			-3
di^2
R(d)^2

Для определения значения коэффициента конкордации проделаем следующие действия. По данным экспертов (табл. 6.50) определим ранг (сумму мест каждой марки хлеба):

r_i = , j= .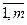

Далее определяем среднее число 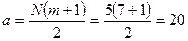, затем

d_i = 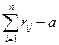, R(d)² = .

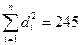Степень согласия экспертов определится по следующей формуле:

R_m(d²) = 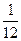N (m³-m) = .

Найдем коэффициент конкордации:

.

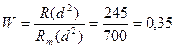Коэффициент конкордации W принимает значения от 0 до 1. Причём он равен 1 при максимальной согласованности и равен 0 при максимальной несогласованности. В нашем примере коэффициент конкордации свидетельствует, что опираться на данные продавцов секции хлеб в принятии решения о закупке марок хлеба, довольно рискованно.

В общем случае, расчет коэффициента конкордации и оценка согласованности мнений экспертов осуществлялась с использованием программного комплекса для обработки статистической информации SPSS.

Композиционный метод бальной оценки. Для многих маркетинговых решений стоит задача необходимости выбора из нескольких альтернатив оптимального решения. Набор критериев отражает весь перечень факторов, определяющих успех реализации альтернатив. Альтернативы оцениваются по одинаковым критериям и одним способом. В бальном методе выбор производится на базе специально отобранных значимых критериев, взвешенных в соответствии с их значением. Оценка производится с помощью шкалы, имеющей от 3 до 10 значений (табл. 7.51).

Таблица 7.51

Матрица бальной оценки силы бизнеса фирм «А» и «В»

Характеристики, влияющие на принятие решения	Относительный вес	Коэффициент	Взвешенная оценка
0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0
«А»	«В»
1. Доля рынка	0,3	· *	0,03	0,06
2. Конкурентная цена	0,15	· *	0,105	0,135
3. Использование инвестиций	0,25	· *	0,062	0,125
4. Эффективность продвижения	0,2	· *	0,04	0,18
5. Уровень конкуренции	0,1	· *	0,03	0,05
Итого:	1,0		0,267	0,55
Шкала оценки: 0 – 0,4 плохо; 0,41 – 0,75 удовлетворительно; 0,76 – 1,0 хорошо
· Фирма «А»; * Фирма «В»

Экстремальное значение шкалы обозначаются «очень сильно», «очень слабо». Общая оценка альтернативы производится путем суммирования оценок по отдельным критериям, умноженным на вес соответствующих критериев. В конце выбирается альтернатива с наибольшим суммарным оценочным значением. Она представляет лучшее значение в данной ситуации. Из взвешенной оценки видно, что сила бизнеса фирмы «В» выше Фирмы «А».

Дата добавления: 2015-03-31