Влияние объема сбыта от затрат на рекламу 1 страница

Номер дочернего предприятия	Затраты на рекламу, тыс. руб.	Объем сбыта, тыс. руб.	Номер дочернего предприятия	Затраты на рекламу, тыс. руб.	Объем сбыта, тыс. руб.

Из общего анализа видно, что увеличение рекламы способствует увеличению объема продаж.

Построение корреляционной таблицы начинают с группировки значений факторного и результативного признаков. Для результативного признака необходимо определить величину интервала. Для этого воспользуемся формулой Стерджера:

h = (y_max – y_min) / (1 + 3,322 lg n) = (1200 – 650) / 5 = 110 тыс. руб.

При формировании первого интервала от минимального значения следует отступить на половину длины интервала и далее формировать интервалы.

В корреляционной таблице факторный признак –x располагается в строках, а результативный y в столбцах. Числа, расположенные на пересечении строк и столбцов означают частоту повторения данного сочетания значения x и y (табл. 7.72).

Таблица 7.72

Расчетная таблица

Центральное значение интервала, y						fx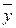
Группы по y     Группы по x	650-760	761-871	872-982	983-1093	1094-1204
							793,8 954,75
fy

Где: f_x – частота повторения данного варианта значения факторного признака во всей совокупности_; f_y –частота повторения результативного признака во всей совокупности. Величина y_i, например, для группы х=21 определится как y₂₁ = (2*750+2*816+1*927)/5=973,8.

Корреляционная таблица дает возможность выдвинуть предположение о наличии или отсутствии связи, а также выяснить ее направление. Если частоты в корреляционной таблице расположены на диагонали из левого верхнего угла в правый нижний угол (т.е. большим значениям фактора соответствуют большие значения функции), то можно предположить наличие прямой корреляционной зависимости между признаками. Если же частоты расположены по диагонали справа налево, то предполагают наличие обратной связи между признаками.

По данным табл. 7.72 построим поле корреляции рассматриваемых факторов (рис. 7.6).

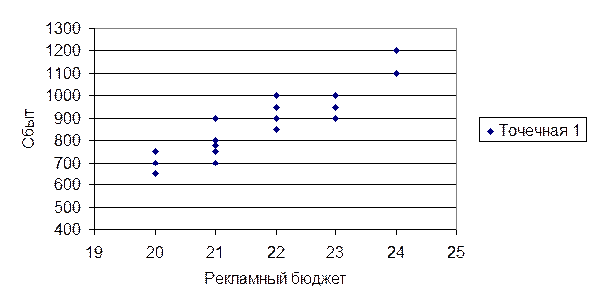
Рис. 7.6. Поле корреляции

Характер распределения случайных величин на поле корреляции свидетельствует о наличии рассматриваемых связей. Итак, увеличение средних значений результативного признака с увеличением значений факторного признака еще раз свидетельствует о возможном наличии прямой корреляционной зависимости объема сбыта от величины рекламы.

Пример 13. Проанализируем и подтвердим или опровергнем утверждение о том, что количество промо-акций проводимых компанией «Колгейт-Палмолив» по продвижению новой зубной щетки увеличивает объем продаж. Для этого проведем выборку территорий (см. табл. 7.73).

Таблица 7.73

Данные о продажах зубной щетки «Colgate 360 Супер чистота» на разных территориях города

№	Территория (код территории)	Объем сбыта (упаковок 12 шт.)	Количество промо-акций

Простейшим приемом обнаружения связи является сопоставление двух параллельных рядов. Из общего анализа видно, что увеличение количества промо-акций способствует увеличению объема продаж.

Другим способом может быть построение поля рассеяния на диаграмме (рис. 7.7).

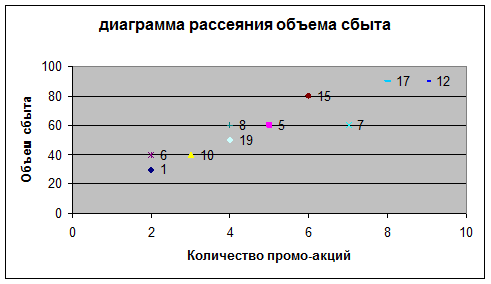
Рис. 7.7. Поле рассеивания

Диаграмма указывает на то, что объем сбыта растет по мере увеличения количества промо-акций.

Альтернативный подход заключается в математическом описании линии, проходящей через точки диаграммы. Эта линия будет соответствовать графику усредненной зависимости. Рассмотрим взаимосвязь между сбытом и числом промо-акций с помощью следующей линейной модели:

,

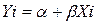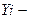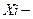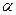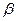где: объем сбыта на i - той территории; количество промо-акций на i -той территории. Расчет параметров и , определяется следующим образом:

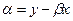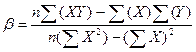, , где , .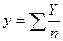

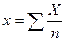Составим таблицу 7.74 с промежуточными вычислениями:

Таблица 7.74

Расчет сумм для вычисления уравнений прямой

№	Объем сбыта, y	Количество промо-акций, x	xy	x^2
∑

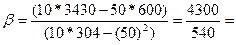7,96; .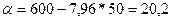

Уравнение имеет вид: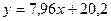

Значение 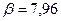, говорит о том, что при проведении каждой дополнительной промо-акции, сбыт увеличивается на 28 упаковок (20,2+7,96).

Средний коэффициент эластичности:

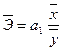; где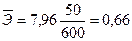

Коэффициент эластичности, равный 0,66, показывает, что с увеличением промо - акций на 1 % - сбыт увеличивается на 0,66%.

Пример 14. Зависимость потребления обуви от возраста потребителей представлена в таблице 7.75. Необходимо выяснить, существует зависимость между потреблением обуви на одного человека в год и возрастом потребителей.

Таблица 7.75

Исходные данные для расчета

Возраст потребителя, лет	Потребление обуви, пар на одного человека в год
До 8	5,0
8 – 16	4,5
17 – 19	5,0
20 – 30	4,5
31 – 40	4,0
41 – 50	3,0
старше 50	2,0
Всего	28,0

Расчеты представим в таблице 7.76. Анализ зависимости потребления обуви от возраста потребителей показывает, что с увеличением возраста потребление уменьшается. Среднее потребление на одного человека составляет четыре пары в год. Если средний возраст потребителей будет увеличиваться (что, кстати, сегодня характерно для России), то следует ожидать уменьшения среднего потребления на одного человека, т. е. спрос на обувь может уменьшиться.

Таблица 7.76

Расчетная таблица

Возраст потребителя, лет (х)	Потребление обуви, пар на одного человека в год (у)	Середина возрастного интервала	хy	x^2	y^2
До 8	5,0		20,0
8 – 16	4,5		54,0		20,25
17 – 19	5,0		90,0
20 – 30	4,5		112,5		20,25
31 – 40	4,0		140,0
41 – 50	3,0		135,0
старше 50	2,0		110,0
Всего	28,0		661,0		119,5

Управленческие решения, основывающиеся на такой информации, связаны с определенным риском, так как анализируемые величины носят вероятностный характер. Для определения степени этого риска рассчитаем коэффициент корреляции:

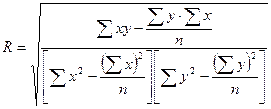
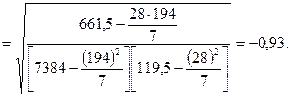
Величина коэффициента корреляции (- 0,93) говорит о том, что между потреблением обуви и возрастом потребителей существует обратная корреляционная зависимость, теснота которой достаточно высока. Следовательно, риск решений, принимаемых на основе анализа этой зависимости, невелик.

Регрессионный анализ дает возможность ответить на вопрос о количественной мере влияния различных факторов на спрос (объем возможной продажи). Он представляет собой подбор и решение математических уравнений, описывающих исследуемые зависимости. Элементы рынка зависят от многих факторов, и формы этих зависимостей могут быть самыми разнообразными. Поэтому регрессионный анализ начинают с построения графика зависимости, на его основе подбирают подходящее математическое уравнение, а затем находят параметры этого уравнения путем решения системы нормальных уравнений.

Регрессионный анализ используется для изучения связей между зависимой переменной и одной или несколькими независимыми переменными. Ранее рассмотренные примеры простой корреляции рекламного бюджета и объема сбыта рассмотрим на примере регрессии. Регрессионный анализ применяют в следующих случаях:

1. Для установления взаимозависимости переменных.

2. Для определения тесноты связи между зависимой и независимыми переменными.

3. Для определения математической зависимости между переменными.

4. Для предсказания значения зависимой переменной.

5. Для определения значимости переменной.

Простейшей системой корреляционной связи является линейная связь между двумя признаками или парная линейная корреляция. Уравнение парной линейной корреляционной связи называется уравнением парной регрессии и имеет вид:

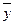= а + bх,

где 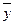- среднее значение результативного признака у при определенном значении факторного признака х; а – свободный член уравнения; b – коэффициент регрессии, измеряющий среднее отношение отклонения результативного признака от его средней величины к отклонению факторного признака от его средней величины на одну единицу его измерения – вариация у, приходящаяся на единицу вариации х.

Пример 15. Администрация торгового предприятия приняла решение о введении нового вида услуг по ценовому стимулированию. По выборке из 10 случаев стимулирования анализируется зависимость выручки продаж в момент стимулирования от затрат на стимулирование (табл. 7.77).

Таблица 7.77

Маркетинговые данные по результатам стимулирования

№ мероприятия
Выручка от продаж, тыс. руб. (У)	26,2	17,8	31,3	23,1	27,5	36,0	14,1	22,3	19,6	31,3
Затраты на стимулирование, тыс. руб. (Х)	3,4	1,8	4,6	2,3	3,1	5,5	0,7	3,0	2,6	4,3

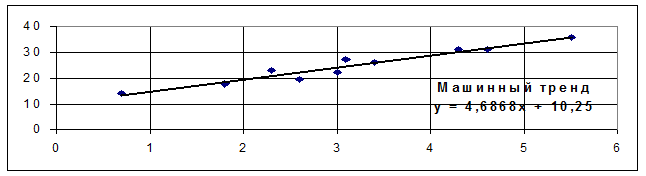
Построим поле корреляции результата и фактора (рис. 7.8).

Рис. 7.8. Поле корреляции результата (выручка от продаж) и фактора (затрат на стимулирование), а так же машинное линейное уравнение регрессии

На основании поля корреляции можно сделать вывод, что между факторным (Х - затраты на стимулирование) и результативным (Y - выручка от продаж) признаками визуально существует прямая зависимость.

Определим методом наименьших квадратов параметры а и b уравнения парной линейной регрессии: у=а+bx. Искомые уравнения имеют вид:

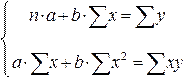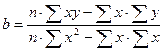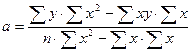где n - число наблюдений в совокупности (в нашем случае 10); a и b - искомые параметры; x и y - фактические значения факторного и результативного признаков. Коэффициенты системы уравнений находим по следующим формулам:

Для облегчения расчетов составим расчетную таблицу 7.78 из пяти граф, в графе 6 дадим выравненное значение y (ŷ). В графах 7,8,9 рассчитаем суммы, которые использованы в формулах пунктов 4, 5 данной задачи.

Таблица 7.78

Расчетная таблица уравнения регрессии

№	X	Y	X²	x·y	y²	ŷ	(y-ŷ)	(x-x)	(ŷ-y)²
1	1	2	3	4	5	6	7	8	9
	3,4	26,2	11,56	686,44	89,08	26,20	0,00	0,0729	1,6384
	1,8	17,8	3,24	316,84	32,04	18,70	0,81	1,7689	36,6884
	4,6	31,3	21,16	979,69	143,98	31,80	0,25	2,1609	47,3344
	2,3	23,1	5,29	533,61	53,13	21,00	4,41	0,6889	15,3664
	3,1	27,5	9,61	756,25	85,25	22,30	7,29	0,0009	0,0144
	5,5		30,25			36,00	0,00	5,6169	122,7664
	0,7	14,1	0,49	198,81	9,87	13,50	0,36	5,9049	130,4164
		22,3		497,29	66,9	24,30	4,00	0,0169	0,3844
	2,6	19,6	6,76	384,16	50,96	22,40	7,84	0,2809	6,3504
	4,3	31,3	18,49	979,69	134,59	30,40	0,81	1,3689	30,0304
∑	31,3	249,2	115,85	6628,78	863,8	249,1	25,77	17,881	390,9900

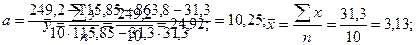Проведем расчеты по следующим формулам:

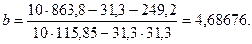Коэффициент регрессии (b) показывает абсолютную силу связи между вариацией x и вариацией y. Применительно к данной задаче можно сказать, что при вкладе в мероприятия по стимулированию продаж на 1 тыс. руб. общая сумма прибавки выручки изменяется в среднем на 4,686 тыс. руб.

Таким образом, линейное уравнение регрессии примет следующий вид: у=10,25+4,68х.

Линейный коэффициент корреляции определяется по формуле:

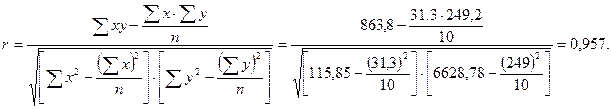В соответствии со шкалой Чеддока можно говорить о высокой тесноте связи между y и x, по значению коэффициента корреляции r = 0.957.

Пример 16. В таблице 7.79 представлены данные о расходах фирмы на рекламу и объеме реализации продукции. Определить тесноту связи между расходами фирмы на рекламу и объемом реализации продукции.

Таблица 7.79

Динамика данных по рекламе и объему реализации товарной продукции

Год	Объем реализации продукции, тыс. руб. (у)	Расходы на рекламу, тыс. руб. (х)
		13,44
		21,65
		24,12
		28,92
Итого		106,13

Решение:

Зависимость определяется линейной функцией следующего вида:

,

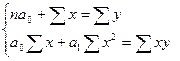Используя данные таблицы, получим систему уравнений:

.

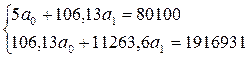Решая систему уравнений, находим коэффициенты: 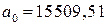, a 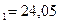. Таким образом, получаем уравнение линейной регрессии:

.

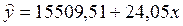Его выражение свидетельствует, что единица расходов на рекламу приносит средний объем реализации продукции 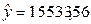тыс. руб.

Коэффициент 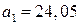называется коэффициентом регрессии и в нашем случае имеет положительный знак, следовательно, связь является прямой. Теснота этой связи к прямой определяется коэффициентом корреляции:

R 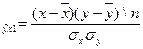, параметры которого рассчитаем по таблице 7.80.

Таблица 7.80

Показатели для расчета коэффициента корреляции

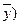
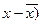
Год	x	y	(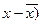y-	(	( (y-	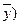(y-	(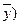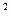
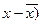
	13,44		-11540	-7,79	89896,6		60,6841
			-7060	-3,23	22803,8		10,4329
	21,65			0,42			0,1764
	24,12			2,89			8,3521
	28,92			7,69			59,1361
	106,13				216728,4		138,7816

Вычислим дисперсии 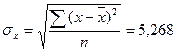, , 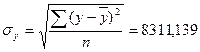тогда коэффициент корреляции определится как 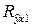= 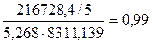. Полученное значение R свидетельствует, что связь довольно тесная.

Пример 17. Рассмотрим основные факторы, влияющие на выбор потребителей при выборе ресторанного комплекса:

- качество обслуживания - это запросы клиентуры, которые определяются в основном объемом, видом и характером услуг, которые предоставляет ресторан своим посетителям;

- социальный статус - эта общая оценка роли человека со стороны общества;

- группа и групповые коммуникации - это группа людей, преследующие общие цели и взаимодействующие для их достижения;

- восприятие - это процесс, с помощью которого люди фильтруют и упорядочивают информацию для формирования значимой картины;

- обучение- это процесс, посредством которого опыт приводит к изменению знаний, отношений и поведения;

- мотивация- это совокупность мотивов и интересов, которыми руководствуется потребитель, принимая решение о предпочтительности товара и целесообразности его применения;

- персональные ценности - это представление потребителей о жизни, о приемлемом поведении;

- жизненный стиль - это различные способы существования потребителей, как они распоряжаются своим временем и деньгами и каковы их товарные предпочтения, отражает деятельность людей, их интересы и мнения;

- ресурсы потребителей - эторесурсы, которые влияют на поведение человека, подразделяются на экономические, временные и познавательные.

- отношение потребителей - это тенденция потребителей оценивать объект благоприятным и неблагоприятным образом.

Степень факторного воздействия оценивается по 5-балльной шкале, где – 5 наиболее сильное влияние.

Проанализируем влияние данных факторов на процесс принятия решения о выборе места отдыха, по мнению руководства и обслуживающего персонала ресторанного комплекса «Х» по данным табл. 7.81.

Таблица 7.81

Оценка степени факторного влияния на процесс решения о покупке

Факторы решения потребителя о покупке	Этапы процесса решения о покупке
А	В	С	D	Е	Итого, факторы
Осознание проблемы	Информационный поиск	Оценка и выбор альтернатив	Покупка	Процессы после покупки
Внешние факторы	1. Группа и групповые коммуникации
2. Социальный статус
3. Качество обслуживания
Внутренние факторы	4. Восприятие
5. Обучение
6. Мотивация
7. Персональные ценности
8. Жизненный стиль
9. Ресурсы потребителей
10. Отношение потребителей
Итого, этапы

Из табл. 7.81 видно, что руководство ресторана наибольшее значение уделяет такому фактору как «Восприятие». Это говорит о том, что политика компании ориентируется прежде всего на то, чтобы создать приятную атмосферу и уютную обстановку для привлечения клиента.

Второе по значению место занимает фактор «Качество обслуживания». Из этого следует, что высший менеджмент и обслуживающий персонал ресторанного комплекса «Х» оказывают клиенту консультационные услуги по выбору блюд, напитков и подробно рассказывая о новых предложениях ресторана.

Дата добавления: 2015-03-31