Технологии определения статистических показателей при анализе маркетинговой информации с применением Microsoft Excel

.

По шкале из табл. 85 это значение соответствует повышенному риску.

Метод Дельфы является наиболее популярным и эффективным методом анкетирования экспертов в определении прогнозов. Он имеет следующие основные особенности:

- на первом этапе каждый эксперт работает изолированно от других;

- опрос экспертов проводится в несколько туров;

- после каждого прошедшего тура экспертов знакомят с оценками других экспертов и их средним значением при сохранении анонимности экспертов и подробной аргументации минимального и максимального значений оценок.

Решение о необходимости проведения последующих туров экспертизы и достоверности групповой оценки принимается, как правило, исходя из показателя согласованности мнений экспертов. В качестве такого показателя используется коэффициент вариации V, который можно рассчитать по формуле ;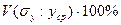

,

где 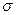- среднее квадратическое отклонение оценок; y_i - индивидуальная оценка каждого эксперта; y_cp - среднее значение оценки; n — число экспертов, участвующих в экспертизе.

В статистике считается, что если V>40%, то это говорит о больших колебаниях и ненадежности средней величины. При определении согласованности мнений экспертов этот предел снижают и, как правило, считают приемлемым коэффициент вариации, не превышающий 33%.

Для лучшего понимания практического использования данного метода рассмотрим конкретный пример.

Пример26. Экспертам было предложено определить сумму закупки товара А, который торговля данного региона ранее не реализовала. Результаты экспертных оценок представлены в таблице 8.49.

Таблица 8.49

Расчетные данные

Порядковый номер экспертной оценки в ранжированном ряду	Первый тур	Второй тур

Требуется проанализировать данные по методу Дельфы.

Решение. После первого тура коэффициент вариации оказался слишком большим (37%) и было принято решение о проведении второго тура. После второго тура экспертизы коэффициент вариации составил около 21%, что свидетельствует о высокой степени согласованности мнений экспертов и возможности использовать среднее значение оценки второго тура (130 млн. руб.) для принятия решения о закупке товара А. Результаты решения условного примера по использованию данного метода подробно излагаются в табл. 8.50.

Таблица 8.50

Порядковый номер экспертной оценки в ранжированном ряду	Первый тур	Второй тур
Итого
Среднее значение оценки (у)
Среднее квадратическое отклонение (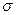)	49,46	27,50
Коэффициент вариации (V), %	37,20	21,15

Для начала работы необходимо установить в Microsoft Excel программной настройки Пакет анализа. Если он уже установлен, то меню Сервис будет содержать пункт подменю Анализ данных. Если данный пункт отсутствует, то необходимо: Сервис – Надстройки; в диалоговом окне Надстройки отметить пункт Пакет анализа; ОК.

1. Построение и графическое отображение интервального вариационного ряда распределения (гистограмма)

Рассмотрим в качестве примера результаты опроса по данным табл. 8.51.

Таблица 8.51

Результаты опроса оптимальной стоимости образовательных услуг.

№ опрошенного	Стоимость образовательных услуг (тыс.руб.)	№ опрошенного	Стоимость образовательных услуг (тыс.руб.)	№ опрошенного	Стоимость образовательных услуг (тыс.руб.)	№ опрошенного	Стоимость образовательных услуг (тыс.руб.)
					23,1
	19,4				17,4
	15,5		23,1
					18,6
							18,5
	16,5
			20,5
			22,5		21,7		16,8
	17,5						25,2
	23,5		19,5
	23,7		21,4		25,5		24,7
	17,5		25,1
			21,5		18,6
			18,5				24,3
							19,6
	18,4						22,7
	22,5		17,7		19,3		22,8

Для выполнения задания необходимо произвести действия с опциями:

1. Перенести данные таблицы № 18 в Excel.

2. Сервис – Анализ данных – Гистограмма – ОК (рис. 8.15).

Рис. 8.15. Окно «Анализ данных»

3. В появившемся диалоговом окне «Гистограмма» задаются следующие параметры: Входной интервал – диапазон ячеек со значениями стоимости образовательных услуг (А2:А81). Интервал карманов – оставить незаполненным. Выходной интервал – любую ячейку (С2). ОК (рис. 8.16).

Рис. 8.16. Окно «Гистограмма» с заполненными параметрами

4. На листе появляется таблица:

Карман	Частота
16,625
19,25
21,875
24,5
27,125
29,75
32,375
Еще

5. В данной таблице необходимо выделить левую верхнюю ячейку (значение 14) и удалить его. Далее в ячейку с именем «Еще» ввести максимальное значение из таблицы, т.е. число 35 и получим новую таблицу:

Карман	Частота
16,625
19,25
21,875
24,5
27,125
29,75
32,375

6. Сервис – Анализ данных – Гистограмма – ОК.

7. В появившемся диалоговом окне «Гистограмма» задаются следующие параметры: Входной интервал – диапазон ячеек со значениями стоимости образовательных услуг (А2:А81). Интервал карманов – диапазон карманов итоговой промежуточной таблицы с верхними границами. Выходной интервал – любую ячейку (С13). Интегральный процент – активизировать. Вывод графика – активизировать. ОК (рис. 8.17).

Рис. 8.17. Окно «Гистограмма» с необходимыми параметрами

8. В результате данных действия на рабочем листе появляется выходная таблица 8.52 и диаграмма (рис. 8.17).

Таблица 8.52

Выходная таблица

Карман	Частота	Интегральный %
16,625		8,75%
19,25		33,75%
21,875		52,50%
24,5		77,50%
27,125		91,25%
29,75		93,75%
32,375		97,50%
		100,00%
Еще		100,00%

Рис. 8.17. Гистограмма и кумулята интервального ряда распределения

Далее необходимо преобразовать выходную таблицу в результативную. Для этого необходимо заменить название столбцов выходной таблицы следующим образом: карман – группа респондентов по стоимости образовательных услуг; частота – число респондентов в группе; интегральный % - накопительная часть группы.

Затем строки первого столбца привести к виду «нижняя граница интервала – верхняя граница интервала», учитывая совпадение верхних границ предыдущего интервала с нижней границей последующего интервала. Строку с именем «Еще» удалить, добавить и заполнить строку «Итого» (табл. 8.53).

Таблица 8.53

Результативная таблица

Группа респондентов по стоимости образовательных услуг	Число респондентов в группе	Накопительная часть группы
15-16,625		8,75%
16,625-19,25		33,75%
19,25-21,875		52,50%
21,875-24,5		77,50%
24,5-27,125		91,25%
27,125-29,75		93,75%
29,75-32,375		97,50%
32,375-35		100,00%
Итого		100,00%

В результате данных преобразований автоматически изменится гистограмма распределения (рис. 8.18).

Рис. 8.18. Преобразованный вид гистограммы и кумуляты интервального ряда распределения стоимости образовательных услуг

2. Расчет описательной статистики (методика 1)

Рассмотрим пример анализа рынка образовательных услуг, а именно оплаты за обучение в Вузах города на экономические специальности. Вводим на рабочий лист в Microsoft Excel данные таблицы 8.54.

Таблица 8.54

Распределение группы студентов по размеру оплаты за образовательные услуги в регионе

Стоимость образовательных услуг, тыс.руб.	Средняя стоимость образовательных услуг, тыс.руб.	Количество респондентов
14-17	15,5
17-20	18,5
20-23	21,5
23-26	24,5
26-29	27,5
29-32	30,5
32-35	33,5

1. В меню выбираем: Сервис Анализ данных Описательная статистика ОК. Появляется окно «Описательная статистика» (рис. 8.19,

8.20).

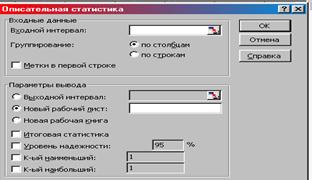Рис. 8.19. Окно «Анализ данных»

Рис. 8.20. Окно «Описательная статистика»

2. В данном окне выбираем команды: Входной интервал – диапазон ячеек со значениями Средняя стоимость образовательных услуг и Количество респондентов (В3:С9); Группировка – по столбцам; Итоговая статистика – активировать, Уровень надежности – активизировать; Уровень надежности – 95%; Выходной интервал – А12; ОК (рис. 8.21).

Рис. 8.21. Окно «Описательная статистка» с необходимыми командами.

При появлении окна с сообщением «Выходной интервал накладывается на имеющиеся данные» - ОК.

В результате указанных действий Microsoft Excel осуществляет вывод таблицы описательных статистик (табл. 8.55).

Таблица 8.55

Описательная статистика

Столбец 1		Столбец 2
Среднее	24,5	Среднее	11,42857
Стандартная ошибка	2,44949	Стандартная ошибка	3,524453
Медиана	24,5	Медиана
Мода		Мода
Стандартное отклонение	6,480741	Стандартное отклонение	9,324826
Дисперсия выборки		Дисперсия выборки	86,95238
Эксцесс	-1,2	Эксцесс	-1,36569
Асимметричность		Асимметричность	0,529414
Интервал		Интервал
Минимум	15,5	Минимум
Максимум	33,5	Максимум
Сумма	171,5	Сумма
Счет		Счет
Уровень надежности(95,4%)	6,1444	Уровень надежности(95,4%)	8,840882

Интерпретация терминов таблицы 8.55 следующая: Среднее – средняя арифметическая величина признака в выборке, вычисленная по несгруппированным данным; Стандартная ошибка – средняя ошибка выборки – среднее квадратическое отклонение выборочной средней от математического ожидания генеральной средней; Медиана – значение признака, приходящееся на середину ранжированного ряда выборочных данных; Мода – значение признака, повторяющееся в выборке с наибольшей частотой; Стандартное отклонение – генеральное среднее квадратическое отклонение, оцененное по выборке; Дисперсия выборки – генеральная дисперсия, оцененная по выборке; Эксцесс – коэффициент эксцесса, оценивающий по выборке значение эксцесса в генеральной совокупности; Ассиметричность – коэффициент ассиметрии, оценивающий по выборке величину ассиметрии в генеральной совокупности; Интервал – размах вариации в выборке; Минимум - минимальное значение признака в выборке; Максимум – максимальное значен ие признака в выборке; Сумма – суммарное значение элементов выборки; Счет – объем выборки; Уровень надежности (95,4%) – предельная ошибка выборки, оцененная с заданным уровнем надежности.

Метод 2. Расчет предельной ошибки выборки при Р=0,997

1. В меню выбираем: Сервис Анализ данных Описательная статистика 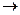ОК. Появляется окно «Описательная статистика».

2. В данном окне выбираем команды: Входной интервал – диапазон ячеек со значениями Средняя стоимость образовательных услуг и Количество респондентов (В3:С9); Итоговая статистика – снять флажок, Уровень надежности – активизировать; Уровень надежности – 99,7%; Выходной интервал – А29; ОК (рис. 8.22).

Рис. 8.22. Окно «Описательная статистка» с необходимыми командами

При появлении окна с сообщением «Выходной интервал накладывается на имеющиеся данные» - ОК.

Таблица 8.56

Предельная ошибка выборки

Столбец 1		Столбец 2
Уровень надежности(99,7%)	11,75814	Уровень надежности(99,7%)	16,91822

Метод 3. Расчет выборочного стандартного отклонения для признака Средняя стоимость образовательных услуг ()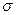

1. Установить курсор в ячейку В33 для среднего квадратического отклонения первого признака (средней стоимости образовательных услуг, тыс.руб.).

2. Вставка Функция. Открывается окно «Мастер функций шаг 1 из 2» (рис. 8.23).

Рис. 8.23. Выбор команды «Функция»

2. Категория Статистические СТАНДОТКЛОНП ОК (рис. 8.24)

3.

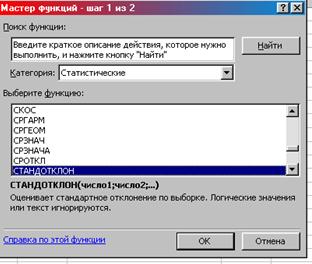Рис. 8.24. Окно «Мастер функций шаг 1 из 2»

4. Появляется окно «Аргументы функции». Число 1 – диапазон ячеек таблицы 1, содержащих значение первого признака (В2:В9) ОК (рис. 8.25). В ячейке В 33 выводится значение стандартного отклонения (6,48).

Рис. 8.25. Окно «Аргументы функции»

Метод 4. Расчет выборочной дисперсии для признака Средняя стоимость образовательных услуг (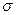 ²)

1. Установить курсор в ячейку В34 для выборочной дисперсии первого признака (средней стоимости образовательных услуг, тыс.руб.).

2. Вставка Функция. Открывается окно «Мастер функций шаг 1 из 2»

3. Категория Статистические ДИСПР ОК (рис. 8.26).

4. Появляется окно «Аргументы функции». Число 1 – диапазон ячеек таблицы № 1, содержащих значение первого признака (В2:В9) ОК. В ячейке В 34 выводится значение дисперсии (42).

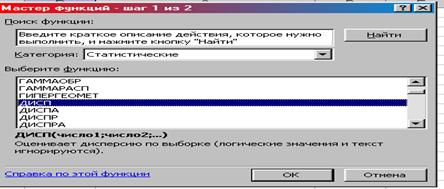Рис. 8.26. Окно «Мастер функций шаг 1 из 2»

Метод 5. Расчет выборочного среднего линейного отклонения для признака Средняя стоимость образовательных услуг (d)

1. Установить курсор в ячейку В35 для выборочной дисперсии первого признака (средней стоимости образовательных услуг, тыс.руб.).

2. Вставка Функция. Открывается окно «Мастер функций шаг 1 из 2»

3. Категория Статистические СРОТКЛ ОК.

4. Появляется окно «Аргументы функции». Число 1 – диапазон ячеек таблицы № 1, содержащих значение первого признака (В2:В9) ОК. В ячейке В 35 выводится значение дисперсии (5,14).

Метод 6. Расчет коэффициента вариации по признаку Средняя стоимость образовательных услуг (V)

1. Установить курсор в ячейку В36 для выборочной дисперсии первого признака (средней стоимости образовательных услуг, тыс.руб.).

2. В активизированную ячейку ввести формулу = В33 / В 14 * 100. Enter. (рис. 9).

3. В ячейке В 36 рассчитывается значение коэффициента вариации (26,452).

Рис. 8.27. Ввод формулы для вычисления коэффициента вариации

Таблица 8.57

Расчетные значения описательных параметров выборочной совокупности

Стандартное отклонение	6,480741
Дисперсия
Среднее линейное отклонение	5,142857
Коэффициент вариации	26,452

Дата добавления: 2015-03-31