
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Прогнозирование рынка методом экономика - математического моделирования
|
|
|
|
Выравнивание по прямой объема прибыли
| Период | Объем прибыли | t | t2 | yt | yt2 | t4 | yt | yi – yt | (yi – yt)2 |
| Апрель | 47,63 | – 4 | – 190,52 | 762,08 | 47,16 | 0,47 | 0,22 | ||
| Май | 46,09 | – 3 | – 138,27 | 414,81 | 52,38 | – 6,29 | 39,56 | ||
| Июнь | 63,90 | – 2 | – 127,80 | 255,60 | 57,02 | 6,88 | 47,33 | ||
| Июль | 62,82 | – 1 | – 62,82 | 62,82 | 61,08 | 1,74 | 3,03 | ||
| Август | 66,31 | 64,56 | 1,75 | 3,06 | |||||
| Сентябрь | 63,92 | 63,92 | 63,92 | 67,46 | – 3,54 | 12,53 | |||
| Октябрь | 67,67 | 135,34 | 270,68 | 69,78 | – 2,11 | 4,45 | |||
| Ноябрь | 69,65 | 208,95 | 626,85 | 71,52 | – 1,87 | 3,50 | |||
| Декабрь | 75,68 | 302,72 | 1210,88 | 72,68 | 3,00 | 9,00 | |||
| ИТОГО | 563,67 | 191,52 | 3667,64 | 0,03 | 122,95 | ||||
| Январь | 73,26 | ||||||||
| Февраль | 73,26 | ||||||||
| Март | 72,68 |
По данным таблицы составим систему уравнений:
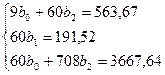
Решая систему уравнений, определим значения параметров уравнения: b0 = 64,56; b1 = 3,19; b2 = – 0,29.
Уравнение параболы выглядит следующим образом:
у = 64,56 + 3,19 t – 0,29 t2
Для прогнозирования объема прибыли от реализации услуги необходимо продолжить столбец 3 (рассматриваемый период t) числами, следующими за указанным числом. В нашем случае – это три, далее рассматриваемый период будет 5, 6, 7. Тогда:
Январь – 64,56 + 3,19 ×5 – 0,29 × 25 = 73,26;
Февраль – 64,56 + 3,19× 6 – 0,29 × 36 = 73,26;
Март – 64,56 + 3,19 × 7 – 0,29 ×49 = 72,68.
Таким образом, с помощью зависимости у = 64,56 + 3,19 t – 0,29 t2 для нелинейного тренда можно прогнозировать ситуацию в будущих периодах.
Экономико-математическое моделирование (ЭММ) в современных условиях все шире используется не только для описания отдельных сторон сложных природных, технических, социальных, экономических и иных явлений, но и для эффективного прогнозирования развития этих явлений в перспективе.
Для прогнозирования рынка могут быть успешно использованы различные виды математических моделей, способных отразить сложные взаимосвязи элементов рынка и влияющих на него факторов. Такие модели, называемые многофакторными (мультифакторными), имеют в основном форму линейных, степенных, логарифмических уравнений.
Приведем в качестве примера наиболее простое из них (и наиболее часто используемое на практике) линейное уравнение множественной регрессии:
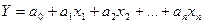 ,
,
где Y — прогноз спроса (возможной продажи); х1, х2,...,хn — факторы, влияющие на развитие рынка; а0, а1, а2,...,аn — параметры уравнения.
Выбрать то или иное уравнение регрессии — это еще не значит построить модель. Для того чтобы построить многофакторную модель, пригодную для прогнозирования рынка, нужно как минимум выполнить следующие работы.
1. Выявить важнейшие факторы, влияющие на развитие рынка.
2. Определить степень влияния выделенных факторов на результативные показатели рыночного процесса, отобрать из них наиболее существенные и сильнодействующие.
3. Разработать математическую форму модели, учитывающую одновременное влияние всех отобранных факторов.
4. Определить состав необходимой исходной информации, характеризующей фактическую динамику развития рынка и влияющие на него факторы, включенные в модель.
5. Организовать и реализовать сбор исходной информации в необходимом для построения модели объеме, обеспечить ее ввод в ЭВМ, подобрать и адаптировать типовые компьютерные программы.
6. Рассчитать математические параметры модели.
7. Провести оценку прогностической ценности модели путем определения величины возможной ошибки прогноза.
8. Рассчитать прогнозные значения возможной продажи товаров.
ЭММ, несомненно, является наиболее современным и прогрессивным методом прогнозирования, пригодным для расчета любых прогнозов в любой области знаний и на любую перспективу. Довольно-таки высокая сложность расчетов при правильном подборе типа многофакторной модели и определении ее параметров при современном уровне развития компьютерной техники не составляет проблемы. Проблема заключается в другом.
С одной стороны, чем больше факторов будет учтено при построении модели, тем адекватнее будет последняя и точнее получится рассчитанный с ее помощью прогноз. Но, с другой стороны, чем больше факторов (х) включается в модель, тем больше должно быть число периодов динамического ряда фактических значений каждого из этих факторов (n). В реальных условиях собрать такую информацию бывает очень сложно или просто невозможно.
Существенным недостатком использования ЭММ является также то, что включить в модель можно только те факторы, которые могут быть подвергнуты количественному измерению. Такие качественные факторы, как мода, уровень культуры и образования, национальные и иные особенности, в математической модели учесть практически невозможно, хотя они и оказывают весьма существенное влияние на формирование покупательского спроса.
В силу этих и некоторых других причин в современных условиях многофакторные модели рынка используют в основном для научных целей, для расчета глобальных прогнозов на высоком уровне обобщения явлений. В практике коммерческих организаций и предпринимательских фирм для прогнозирования рынка (спроса) в основном применяются одно- двухфакторные модели, в которых учитывается наиболее сильнодействующий фактор (цены, доходы населения, демографические показатели) и тенденция его изменения во времени. Например:
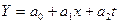 ,
,
где Y — прогноз спроса (возможной продажи); х — фактор, влияющий на спрос; t — время; а0, a1, a2 — параметры модели.
Рассмотрим конкретные примеры.
Пример 19. Имеются следующие данные по объему сбыта предприятия (табл. 8.38):
Таблица 8.38
Данные для анализа
| Год | ||||||
| Объем сбыта (млн. руб.) | 13,5 | 14,2 | 13,7 | 15,0 | 12,7 | 14,9 |
Необходимо дать количественную модель, выражающую основную тенденцию изменения уровней динамического ряда во времени, используя аналитическое выравнивание ряда динамики.
Решение. Для выравнивания данного ряда используем линейную трендовую модель – уравнение прямой: 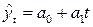 . Параметры уравнения находим по формулам:
. Параметры уравнения находим по формулам:
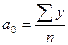 ;
; 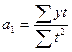 ,
,
где n – число уровней, у нас n =6. Решение проведем в таблице 8.39.
Таблица 8.39
| Год | Объем сбыта (млн. руб.), у | t | t2 | yt | 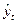
| 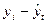
| 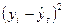
|
| 13,5 | -5 | -67,5 | 13,75 | -0,25 | 0,0625 | ||
| 14,2 | -3 | -42,6 | 13,85 | 0,35 | 0,1225 | ||
| 13,7 | -1 | -13,7 | 13,95 | -0,25 | 0,0625 | ||
| 15,0 | +1 | 15,0 | 14,05 | 0,95 | 0,9025 | ||
| 12,7 | +3 | 38,1 | 14,15 | -1,45 | 2,1025 | ||
| 14,9 | +5 | 74,5 | 14,25 | 0,65 | 0,4225 | ||
| Итого |

|

| 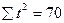
| 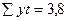
|
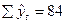
|
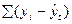 =0 =0
|  = 3,675 = 3,675
|
Подставляя значения из таблицы получает: 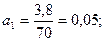
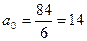 .
.
Уравнение прямой, представляющее собой трендовую модель искомой функции, будет иметь вид: 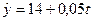 . Подставляя в данное уравнение последовательно значения t, равные -5,-3,-1,+1,+3,+5, находим выровненные уровни
. Подставляя в данное уравнение последовательно значения t, равные -5,-3,-1,+1,+3,+5, находим выровненные уровни 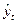 . Проверяем условие
. Проверяем условие 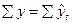 . Оно верно, что свидетельствует о правильности найденных значений уровней выровненного ряда. Фактические значения объема сбыта представим в виде графика на рис. 8.13.
. Оно верно, что свидетельствует о правильности найденных значений уровней выровненного ряда. Фактические значения объема сбыта представим в виде графика на рис. 8.13.
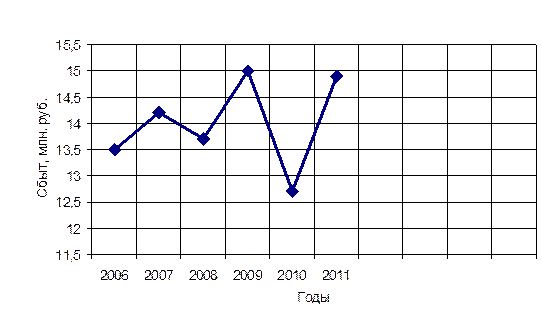
Рис. 8.13. Фактические значения объема сбыта
Соединив точки, построенные по фактическим данным, получим ломаную линию, на основании которой затруднительно вынести суждение о характере общей тенденции в изменении объема сбыта.
Построим расчетные (выровненные) значения на рис. 8.14.
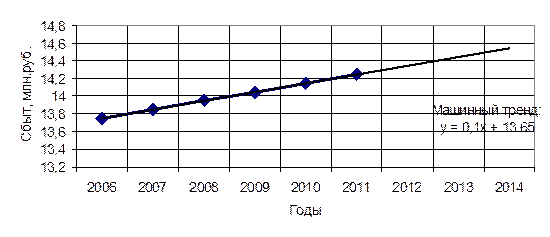
Рис. 8.14. Выровненные значения объема сбыта
Полученное уравнение  согласуется с показателями машинного тренда и показывает, что с 2006 по 2011 год наблюдалась тенденция увеличения сбыта в среднем на 0,05 млн. руб. Однако это высказывание не устанавливает: рост продаж обусловлен ростом профессионализма маркетологов или ростом цен на товары.
согласуется с показателями машинного тренда и показывает, что с 2006 по 2011 год наблюдалась тенденция увеличения сбыта в среднем на 0,05 млн. руб. Однако это высказывание не устанавливает: рост продаж обусловлен ростом профессионализма маркетологов или ростом цен на товары.
Пример 20. По данным предыдущей задачи провести экстраполяцию значений сбыта.
Решение. Определим ожидаемый объем сбыта в 2009 году, подставив в уравнение значение t =7. Тогда 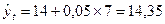 млн. руб. Это точечная оценка прогнозируемого значения.
млн. руб. Это точечная оценка прогнозируемого значения.
Найдем интервальную оценку при доверительной вероятности 0,95. Для определения границ интервалов используем формулу:
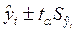 ,
,
где 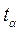 - коэффициент доверия по распределению Стьюдента;
- коэффициент доверия по распределению Стьюдента; 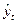 - остаточное среднее квадратическое отклонение от тренда (
- остаточное среднее квадратическое отклонение от тренда (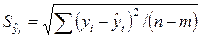 , где n – число уровней ряда динамики; m – число параметров адекватной модели тренда (для уравнения прямой m =2)).
, где n – число уровней ряда динамики; m – число параметров адекватной модели тренда (для уравнения прямой m =2)).
В нашем случае 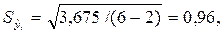 тогда интервальная оценка:
тогда интервальная оценка:
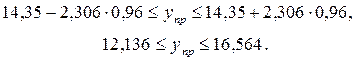
Следовательно, с вероятностью, равной 0,95, можно утверждать, что объем сбыта в 2009 году будет не менее 12,136 млн.руб. и не более 16,564 млн.руб.
Пример 21. Определим прогноз развития рынка бытовой техники в регионе Х по данным таблицы 8.40.
Таблица 8.40
Объем регионального рынка продаж бытовой техники
за период 2006 - 2011 гг.
| Год | ||||||
| Объем рынка (млн.$) |
Примем: y  -объем телевизионной рекламы;x – рассматриваемый период; a-объем рекламы при нулевом периоде (x=0); b- ежегодный прирост. Для расчетов трендовых величин составим таблицу 8.41.
-объем телевизионной рекламы;x – рассматриваемый период; a-объем рекламы при нулевом периоде (x=0); b- ежегодный прирост. Для расчетов трендовых величин составим таблицу 8.41.
Таблица 8.41
Расчетная таблица
| Год | Объем рынка (y) | x | x 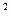
| xy | y 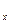
|
| -5 | -950 | 8,5 | |||
| -3 | -810 | 335,1 | |||
| -1 | -510 | 661,7 | |||
| +1 | 988,3 | ||||
| +3 | 1314,9 | ||||
| +5 | 1641,5 | ||||
| Σ | |||||
| +7 | 1968,1 | ||||
| +9 | 2294,7 | ||||
| +11 | 2621,3 |
Полученные значения подставим в формулы для нахождения a и b:
а = 4950/6=825, b =11340/70=163,3. Следовательно, линейное уравнение прямой, представляющее собой трендовую модель искомой функции, будет иметь вид: y 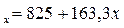 Подставляя в данное уравнение последовательно значения x, равные: -5,-3,-1,+1.+3,+5, находим выровненные уровни y
Подставляя в данное уравнение последовательно значения x, равные: -5,-3,-1,+1.+3,+5, находим выровненные уровни y 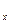
y 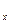 (2006)= 825+163,3*(-5)=825-816,5= 8,5
(2006)= 825+163,3*(-5)=825-816,5= 8,5
y 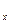 (2007)= 825+163,3*(-3)=825-489,9= 335,1
(2007)= 825+163,3*(-3)=825-489,9= 335,1
y 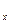 (2008)= 825+163,3*(-1)=825-163,3= - 661,7
(2008)= 825+163,3*(-1)=825-163,3= - 661,7
y 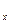 (2009)= 825+163,3*1=988,3
(2009)= 825+163,3*1=988,3
y 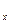 (2010)= 825+163,3*3=825+489,9=1314,9
(2010)= 825+163,3*3=825+489,9=1314,9
y 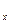 (2011)= 825+163,3*5=825+816,5=1641,5
(2011)= 825+163,3*5=825+816,5=1641,5
В данном случае Σy=Σyx =4950. Следовательно, значения уровней выровненного ряда найдены верно.
Для прогнозирования объемов регионального рынка необходимо продолжить рассматриваемый период (x) числами, следующими за указанным числом. В данном случае – это 5, далее рассматриваемый период будет 7, 9, 11. Следовательно, величина прогноза развития рекламного рынка телевизионной рекламы определится как:
y 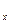 (2012)= 825+163,3*7=825+1143,1=1968,1;
(2012)= 825+163,3*7=825+1143,1=1968,1;
y 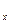 (2013)= 825+163,3*9=825+1469,7= 2294,7;
(2013)= 825+163,3*9=825+1469,7= 2294,7;
y 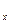 (2014)= 825+163,3*11=825+1796,3= 2621,3.
(2014)= 825+163,3*11=825+1796,3= 2621,3.
Таким образом, можно предположить, что к 2014 году региональные продажи бытовой техники могут составить около 2700 млн. дол. при среднем темпе инфляции, если не учитывать фактор насыщения ею и появление товаров заменителей.
Пример 22. Прогнозирование по показательной функции используется в тех случаях, когда ряд отражает развитие в геометрической прогрессии, т.е. когда цепные коэффициенты роста практически постоянны. Для выравнивания зависимости может использоваться парабола второго порядка:
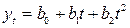 .
.
Значения b0 и b1 идентичны параметрам используемым в линейном тренде. Параметр b2 характеризует постоянное изменение интенсивности развития (в единицу времени). При b2> 0 происходит ускорение развития, при b2 <0 идет процесс замедления роста.
Система нормальных уравнений для нахождения параметров уравнения параболы имеет вид:
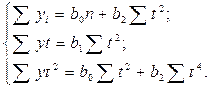
Решив систему уравнений, определим значения параметров параболы второго порядка. Рассмотрим построение линии тренда по параболе исходя из данных табл. 8.42).
Таблица 8.42
Выравнивание по прямой объема выручки
| Квартал | Выручка, тыс. руб. | t | t2 | yt | yt2 | yi-yt | (yi-yt)2 | t4 | yt |
| I | -1,5 | 2,25 | -750 | -5 | 5.063 | ||||
| II | -0,5 | 0,25 | -290 | -5 | 0.063 | ||||
| III | 0,5 | 0,25 | -5 | 0.063 | |||||
| IV | 1,5 | 2,25 | 5.063 | ||||||
| ИТОГО: | 10.252 |
По данным таблицы 8.42 составим систему уравнений:
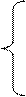 4b0 + 5b2 = 2520;
4b0 + 5b2 = 2520;
5b1 = 450;
5b0 + 10.252b2 = 209250.
Решая систему уравнений, определим значения параметров уравнения: b0 = 558,2; b1 = 90; b2 = 57,41
Уравнение нелинейного тренда выглядит следующим образом:
у = 558,2 + 90t + 57,41t2.
Вероятностные границы интервала прогнозируемого явления определяются как (yt – taS)< ynp < (yt + taS), где ta – коэффициент доверия по распределению Стьюдента; S – остаточное среднеквадратическое отклонение от тренда:
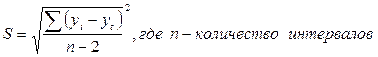 .
.
На основании данных таблицы 8.42 при доверительной вероятности 0,95 и уровне значимости 0,05, коэффициент доверия ta = 2,306 (по таблице Стьюдента) 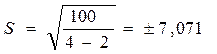
По данным таблицы 8.42 и уравнения тренда у = 558,2 + 90t + 57,41t2, при t = 6,7 определим ожидаемый объем выручки на I-й и II-й кварталы года.
YI = 558,2 + 90*6 + 57,41*36 = 3164,96 тыс. руб.;
YII = 558,2+ 90*7 + 57,41*42 = 3629,42 тыс. руб.
Определим вероятностные границы разброса прогнозируемого значения:
а) по I кварталу: 3164,96 – 2,306*7,071< ynp I< 3164,96 + 2,306*7,071 или 3148,65< ynp I < 3181,266;
б) по II кварталу: 3629,42 – 2,306*7,071 < ynp II < 3629,42 + 2,306*7,071 или 3613,11 < ynp II < 3645,72.
Следовательно, с вероятностью в 0,95 можно утверждать, что объем выручки в первом квартале будет не менее 3148,65 тыс. руб., но и не более 3181,266 тыс. руб., а во втором – не менее 3613,11 тыс. руб., но и не более 3645,72 тыс. руб.
|
|
|
|
|
Дата добавления: 2015-03-31; Просмотров: 507; Нарушение авторских прав?; Мы поможем в написании вашей работы!