
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Выравнивание по прямой объема продаж
|
|
|
|
| Месяц | Уровень продаж, млн. руб. – yi | 
| 
| yt | 
| 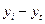
| 
|
| Январь Февраль Март Апрель Май Июнь | -5 -3 -1 | -60 -30 -14 | 13,03 12,64 12,46 12,46 11,80 11,61 | -1,03 -2,64 1,54 -1,46 3,2 0,39 | 1,06 6,96 2,37 2,13 10,24 0,152 | ||
| Итого | 
| 
| 
| 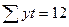
| 
|  0 0
|  22,91 22,91
|
Коэффициенты линейного уравнения тренда для нашего примера имеют вид:

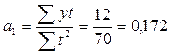 .
.
Коэффициент а1 характеризует уменьшение объема продаж на 0,172 млн. руб. в месяц. Уравнение прямой, представляющее собой трендовую модель искомой функции (тенденции изменения объема месячных продаж), будет иметь вид: у = 12,33 + 0,172t. С помощью этой зависимости можно прогнозировать ситуацию в будущих периодах.
Вероятностные границы интервала прогнозируемого явления определятся как  , где ta – коэффициент доверия по распределению Стьюдента; S – остаточное среднеквадратическое отклонение от тренда:
, где ta – коэффициент доверия по распределению Стьюдента; S – остаточное среднеквадратическое отклонение от тренда:
 , где n – количество интервалов.
, где n – количество интервалов.
На основании данных табл. 6.17, при доверительной вероятности 0,95 и уровне значимости 0,05, коэффициент доверия ta = 2306 (по таблице Стьюдента). Тогда  S =
S = 
Продление в будущее тенденции, наблюдавшейся в прошлом, носит название экстраполяции. По данным табл. 6.17 можно определить ожидаемый уровень продаж в июле месяце (исходя уравнения у = 12,33 + 0,172t, при t = 7).
Зная точечную оценку прогнозируемого значения объема продаж на июль месяц - Уиюль = 12,33 + 0,172*7 = 13,53, определим вероятностные границы интервала продаж: 13,53-2,306*2,39  упр
упр  13,53+2,306*2,39, или 8,018
13,53+2,306*2,39, или 8,018  упр
упр  19,04. Следовательно с вероятностью в 0,95 можно утверждать, что объем продаж в июле месяце будет не менее 8,018 млн. руб., но и не более 19,04 млн. руб.
19,04. Следовательно с вероятностью в 0,95 можно утверждать, что объем продаж в июле месяце будет не менее 8,018 млн. руб., но и не более 19,04 млн. руб.
Пример 17. Требуется рассчитать объем потребления условного товара А в 8-м и 9-м годах (прогноз) в расчете на одного потребителя, используя фактические данные о потреблении за семь лет, которые приведены во второй графе таблицы 8.36.
Условные обозначения таблицы: t - порядковый номер года; у - фактическое потребление товара на одного человека; уp - выровненные (расчетные, теоретические) значения потребления; n - количество членов (периодов) в динамическом ряду.
Вначале решения проводим графический анализ тенденции развития динамического ряда, в результате которого можно сделать предварительный вывод о том, что данная тенденция лучше всего описывается уравнением прямой линии уt = a0 + a1t.
Таблица 8.36
Расчетная таблица
| t | y | t2 | y ∙ t | yp | y - yp | (y - yp)2 |
| 1-й 2-й 3-й 4-й 5-й 6-й 7-й | 6,5 6,6 6,8 7,1 7,2 7,3 7,5 | 6,5 13,2 20,4 28,4 36,0 43,8 52,5 | 6,5 6,7 6,8 7,0 7,2 7,4 7,5 | -0,1 0,1 -0,1 | 0,01 0,01 0,01 | |
| 49,0 | 200,8 | - | - | 0,03 |
Параметры прогнозного уравнения можно определить, решив систему нормальных уравнений следующего вида:
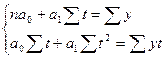
 .
.
Если из второго уравнения вычесть первое, то получится, что а1 = 0,17. Подставив а1 в любое из предыдущих уравнений, можно определить значение параметра а0 = 6,32. Тогда прогнозное уравнение приобретает вид:
 .
.
Пригодность этого уравнения для прогнозирования (его прогностическую ценность) можно определить, например, путем расчета выровненных (теоретических) значений и сравнения их с фактическими (рис. 8.12). Так,
 ,
, 
и т. д. по каждому ряду. Сравнение выровненных (расчетных) и фактических значений потребления методом наименьших квадратов свидетельствует о том, что подобранное уравнение весьма точно описывает фактическую тенденцию и может быть использовано для прогнозирования. Средняя ошибка прогноза, рассчитанная по формуле
 , где
, где  ,
,
говорит о высокой точности рассчитываемых прогнозов. Значения этих прогнозов составят: на 8-й год: 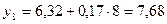 шт.; на 9-й год:
шт.; на 9-й год:  шт.
шт.
 |
Рис. 8.12. Динамика продажи товара в расчете на одного потребителя
в 1 – 7-м годах
Достоинства метода экстраполяции заключаются прежде всего в сравнительной несложности расчетов и небольшом объеме первичной информации. Основной недостаток этого метода связан с тем, что при его применении спрос (потребление) рассматривается только как функция времени и не учитывается влияние различных других факторов. Поэтому экстраполяция применима лишь для краткосрочного рыночного прогнозирования.
Пример 18. Рассмотрим применение нелинейного тренда по данным табл. 8.37. Для выравнивания зависимости может использоваться парабола второго порядка: yt = b0 + b1t + b2t2.
Значения b0 и b1 идентичны параметрам, используемым в линейном тренде. Параметр b2 характеризует постоянное изменение интенсивности развития (в единицу времени). При b2 > 0 происходит ускорение развития, при b2 < 0, идет процесс замедления роста.
Система нормальных уравнений для нахождения параметров уравнения параболы имеет вид:
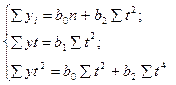
Решив систему уравнений, определим значения параметров уравнения параболы второго порядка.
Таблица 8.37
|
|
|
|
|
Дата добавления: 2015-03-31; Просмотров: 590; Нарушение авторских прав?; Мы поможем в написании вашей работы!