Евклидовы пространства. 16. Дайте определение скалярного произведения в пространстве

16. Дайте определение скалярного произведения в пространстве 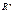. Приведите неравенство Коши-Буняковского и проиллюстрируйте его на примере.

Скалярным произведением векторов х,у принадлеж. R ⁿ: x=(x₁,…,x_n), y=(y₁,…y_n) называется число (х,у)=

Для любых двух векторов евклидова пространства справедливо неравенство Коши-Буняковского:
І(а, b)І ≤ ІaІ ІbІ

Пример: x = (−1, 0), y = (4, 3) ∈ R2:

(x, y)=(−1)·4+0·3 = −4, |x|=1, |y|=√16 + 9 = 5

|(x, y)| = 4 ≤ 5 = |x|·|y|

17. Докажите, что для любых векторов 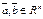верно неравенство треугольника .

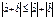Для любых двух векторов а и b в евклидовом пространстве справедливо соотношение, называемое неравенством треугольника:

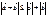
Доказательство:

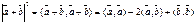
В силу неравенства Коши-Буняковского, согласно которому ,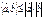

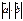²+2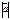 + ²=( + )²

Извлечем корень из обеих частей этого неравенства без потери знака, т.к. обе части заведомо положительны.

Получим: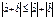

18. Дайте определение ортонормированной системы векторов в 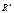. Приведите пример ортонормированной системы в .

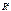Система векторов v1,...vn называется ортонормированной, если ∀i, j = 1..n выполняется:(vi, vj) = δij, где δij =1 0, i = j;, i не равно j. − символ Кронекера.

Пример ортонормированной системы в R3:

x = (1, 0, 0), y= (0, 1, 0), z= (0, 0, 1)

(x, y) = (y, z) = (x, z) = 0, (x, x) = (y, y) = (z, z) = 1

19. Докажите, что ортонормированная система в 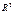, состоящая из 3 векторов, является базисом пространства .

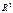Пусть x, y, z ∈ R3 - система ортонормированных векторов: (x, y) = (y, z) = (x, z) = 0, (x, x) = (y, y) = (z, z) = 1

Предположим, что система векторов линейно зависима, то есть z = αx + βy. Тогда 0 = (z, x) = (αx + βy, x) = α(x, x) + β(x, y) = α

Мы получили, что α = 0, то есть z = βy. Аналогично 0 = (z, y) = (βy, y) = β(y, y) = β

Мы получили, что α = β = 0, a значит, z = 0, что противоречит с тем условием, что (z, z) = 1. Противоречие означает, что система ортонормированных векторов x, y, z ∈ R3 -линейно независима, что означает, что система трех линейно независимых векторов x, y, z

является базисом в пространстве размерности 3.

20. Дайте определение ортогонального базиса в 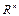. Приведите пример ортогонального базиса в 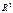, не содержащего ни одного из векторов стандартного базиса 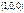, , 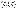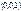. Ответ обоснуйте.

Ортогональный (ортонормированный) базис — ортогональная (ортонормированная) система элементов линейного пространства со скалярным произведением, обладающая свойством полноты. Ортогональный базис — базис, составленный из попарно ортогональных векторов. Этот базис линейно независим. Пример ортогонального базиса в R3: v1=(3;0;0), v2=(0;-2;0), v3=(0;0;3). Так как (v1, v2) = (v2, v3) = (v1, v3) = 0.

Дата добавления: 2015-03-31