Дайте определение линейного пространства. Приведите примеры линейных пространств

Линейные пространства

Опр. Линейное пространство - это множество элементов, для которого определены операции сложения векторов и умножения вектора на число. Указанные операции должны удовлетворять следующим условиям:

1) a + b = b + a
2) (a + b)+c = a+(b + c)
3) a + 0 = a
4) a + (-a) = 0
5) k (a + b) = ka + kb
6) (k + m) a = ka + ma
7) k(ma) = (km)a
8) 1*a = a

Где a, b, c – произвольные векторы;
k, m – произвольные действительные числа

Примеры линейных пространств:

1) пространство Rⁿ;

2) множество решений однородной системы линейных уравнений;

3) множество функций, определенных на отрезке [a;b], с заданными для них обычным образом операциями сложения и умножения на число;

4) множество положительных чисел, если операцию сложения двух элементов x и y определить как их произведение (понимаемое в обычном смысле), а операцию умножения х на действительное число k - как возведение x в степень k;

5) множество всех многочленов с заданными для них стандартным образом операциями сложения и умножения на число;

6) множество всех многочленов, степень которых не превышает n.

2. Дайте определение линейно зависимой системы векторов. Приведите примеры. Будет ли линейно зависима система, включающая нулевой вектор? Ответ обоснуйте.

Система векторов а₁, а₂ и а_m называется линейно зависимой, если существуют такие числа с₁, с₂, с_m (не равные нулю одновременно) и выполняется равенство:

с₁ā₁+с₂ā₂+...+с_mā_m =0.

Пример:

а₁ = (2, 2, 3)
а₂ = (0, -4, 5)
а₃ = (3, 13, -8) – система векторов.

Пусть с₁ = 3, с₂ = -5, с₃ = -2, тогда 3а₁ - 5а₂ - 2а₃ = (6, 6, 9) – (0, -20, 25) – (6, 26, -16) = (0, 0, 0)

Вывод: система векторов линейно зависимая.

Утверждение: Если часть системы линейно зависима, то и вся система линейно зависима.
Следствие: Система, включающая нулевой вектор, линейно зависима.

Док-во: Пусть дана система из трех векторов а₁, а₂, а₃, причем часть системы, состоящая из векторов а₂, а₃ – линейно зависима, т. е. справедливо равенство:
с₂ а₂ + с₃ а₃ = 0; с₂, с₃ ≠ 0.
Добавим к обеим частям нулевой вектор а₁, получим:
0а₁ + с₂ а₂ + с₃ а₃ = 0, что означает линейную зависимость такой системы.

1. Система из одного вектора а линейно зависима тогда когда а=0

2. Система содержащая более одного вектора линейно зависима в том и только в том случае когда среди данных векторов имеется такой который линейно выражается через все остальные

3. Если часть системы линейно зависима то и вся система линейно зависима, система включающая нулевой ветор линейно зависима

4. Если система линейно независима но при добавлении к ней а становится зависимой то а линейно выражается через другие векторы

3. Дайте определение линейно независимой системы векторов. Приведите примеры. Будет ли линейно независимой лестничная система векторов? Ответ обоснуйте.

Система векторов ā1,ā2,…,ām такова, что равенство с1ā1+с2ā2+...+сmām =0 возможно только при с1=c2=,..,=с3=0, то эта система называется линейно независимой.

Пример:

а = (а₁, а₂, …, а_n)
b = (0, b₂,…, b_n)
c = (0, 0, c₃, …, c_n) – лестничная система векторов.

Любая лестничная система векторов линейно независима.

Док-во: От противного. Предположим, что лестничная система векторов линейно зависима. Тогда один из данных векторов должен линейно выражаться через остальные. Пусть а выражается через b и c. Тогда:
а = kb + mc
Но такое равенство невозможно, так как первая координата вектора а отлична от нуля, а первая координата вектора kb + mc равна нулю. Данное противоречие доказывает, что система векторов а, b, c – линейно независима.

Примеры:

ü Система векторов ·i, j линейного пространства R2 геометрических радиусов векторов плоскости линейно независима.Действительно.

i = (1, 0), j = (0, 1), С1·i + С2· j = (С1, С2), а из (С1, С2) = 0 следует, что С1 = 0 и С1 = 0, т.е. система векторов i, j из R2 линейно независима.

ü В линейном арифметическом пространстве Rn рассмот-

рим n векторов e 1 = (1, 0,..., 0), e 2 = (0, 1,..., 0, 0),..., e n = (0, 0,.., 0, 1). До-

кажем, что система этих векторов линейно независима.

Так как для любых коэффициентов α1, α2,..., αn линейная комбина-

ция α1 e 1 + α2 e 2 +... + αn e n = (α1, α2,..., αn), то ясно, что она может быть

равна нулевому вектору (0, 0,..., 0) только при условии равенства нулю

всех коэффициентов. По определению, это означает, что система векторов

линейно независима.

4. Дайте определение базиса линейного пространства. Докажите, что координаты вектора в данном базисе определены однозначно.

Система векторов а₁, а₂, …, а_n называется базисом линейного пространства V, если выполнены следующие условия:
1) эти векторы линейно независимы;
2) любой вектор а из V является линейной комбинацией векторов данной системы, т. е.
а = k₁ а₁ + k₂ а₂ + … + k_n а_n

Предложение: координаты вектора в данном базисе определены однозначно.
Док-во: пусть существует два разложения данного вектора а по базису а₁, а₂, …, а_n
а = k₁ а₁ + k₂ а₂ + … + k_n а_n
а = l₁ а₁ + l₂ а₂ + … + l_n а_n

Так как левые части равны, то правые также равны:
k₁ а₁ + k₂ а₂ + … + k_n а_n = l₁ а₁ + l₂ а₂ + … + l_n а_n
(k₁ - l₁) а₁ + (k₂ - l₂) а₂ + …+ (k_n - l_n) а_n = 0

Так как векторы базиса линейно независимы, то k₁ - l₁ = 0 → k₁ = l₁

ч. т. д.

5. Что называется размерностью линейного пространства 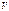? Может ли система из 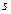векторов, где 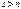, являться базисом 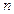- мерного пространства ? Ответ обоснуйте.

Размерностью пространства V называется число векторов его базиса. Размерность пространства V обозначается через dimV. Линейное пространство, имеющее размерность n, называют n-мерным.

В n-мерном пространстве V любая система из s векторов, где s>n, линейно зависима. А из определения базиса линейного пространства следует, что система векторов должна быть линейно независима. Следовательно, система из s векторов, где s>n, не может являться базисом n-мерного пространства V.

6. Пусть - векторы из 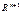. Можно ли составить базис пространства 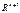из линейных комбинаций этих векторов? Ответ обоснуйте.

Нет, нельзя. Так как размерность Rn+1 равна n + 1, то любой базис пространства Rn+1 должен содержать n + 1 линейно независимых векторов. Пусть a1,...an - линейно независимы и входят в некоторый базис {a1,...an, an+1} пространства. Но тогда вектор an+1 нельзя получить с помощью линейной комбинации векторов a1,...an, так как в этом случае система векторов a1,...an, an+1 будет линейно зависимой, что противоречит определению базиса.

7. Дайте определение подпространства линейного пространства и приведите пример. Как связаны размерности пространства и его подпространства? Ответ обоснуйте.

Подпространством линейного пространства R над полем K называется любое непустое подмножество M этого пространства, на котором корректны операции сложения элементов и умножения элемента на число, которые введены в исходном линейном пространстве R.

Примеры подпространств:

1) Прямая (подпространство) на плоскости (пространство)

2) Плоскость (подпространство) в пространстве R³ (пространство)

3) Все матрицы вида ab, a = -d, подпространство пространства всех c-a матриц 2х2

Одно из свойств подпространств говорит о том, что размерность подпространства не превосходит размерности самого пространства (так как подпространство является подмножеством пространства).

Теор. Подпр-во является линейным пр-вом

1) Для любых двух векторов а, в, из S их сумма также принадлежит лин пространству

2) Произведение а на действительное число тоже принадлежит данному пространству

Размерность родпростарнства S (неравно 0) меньше пр-ва V. Если бы их размерность была равна, то базис подпространства S являлся бы базисом V, Следовательно S и V совпали бы.

8. Какие из множеств, образованных всевозможными векторами из 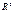такими, что а) 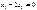, б) , в) 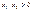, являются подпространствами в 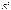, а какие нет? Ответ обоснуйте.

а) задает подпространство M, так как это уравнение определяет прямую (одномерное подпространство) на плоскости, проходящее через (0,0) и для него выполнены условия подпросранства.

б) не задает подпространства, так как нарушается 2ое условие: Пример: x = (1, 0) 2 M.

При этом 2 · x = (2, 0) не принадлежит M.

в) не задает подпространства, так как нарушается первое условие

Дата добавления: 2015-03-31